平均13.1点（満点22点）
問題はコチラ→愛知全県模試さん
Ｂグループは別ページ。
大問１（小問集合）
（１）
８－（２－５）
＝８－（－３）
＝８＋３＝11
（２）
（５ｘ＋３）/３－（３ｘ＋２）/２
＝{２（５ｘ＋３）－２（３ｘ＋２）}/６
＝１/６ｘ
（３）
√３（√５－３）＋√27
＝√15－３√３＋３√３
＝√15
（４）
12ｘ2ｙ×（－３ｙ）2÷（２ｘｙ）2
＝27ｙ
（５）
（ｘ＋３）（ｘ－８）＋４（ｘ＋５）＝０
ｘ2－５ｘ－24＋４ｘ＋20
＝ｘ2－ｘ－４＝０
因数分解できないので、解の公式を適用。
ｘ＝{１±√（－１）2－４・１・（－４）}/２
＝（１±√17）/２
（６）
リボンの全体はｘｃｍ
切り取る長さは15ａｃｍ
余りなしで切り取れたらｘ＝15ａとなるので、
ｘ≧15ａ
（７）
ｘ＝４のとき、ｙ＝８
ｘ＝６のとき、ｙ＝18
（18－８）/（６－４）＝５
*ｙ＝ａｘ2のグラフで、ｐ→ｑの変化の割合はａ（ｐ＋ｑ）
１/２（４＋６）＝５
（８）
全体の人数を１とおいたとき、7.4～7.8の人数は0.15。
120×0.15/１＝１８人
（９）
△ＡＢＥ∽△ＣＥＤを利用。
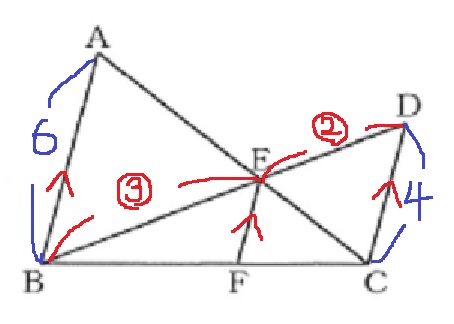
ＢＥ：ＥＤ＝６：４＝３：２
ここから△ＢＦＥ∽△ＢＣＤへ。
ＥＦ：ＤＣ＝３：５
ＥＦ＝４×３/５＝12/５ｃｍ
大問２（小問集合２）
（１）
ア＝ｎとおくと、イ＝ｎ＋２。
ｎ（ｎ＋２）
＝ｎ2＋２ｎ＝899
ｎ2＋２ｎ－899＝０
しかし、899の素因数をみつけるのが大変。。
奇数の文字式は２ｎ－１でも表せるので、
ア＝２ｎ－１、イ＝２ｎ＋１とおき、
（２ｎ－１）（２ｎ＋１）
＝４ｎ2－１＝899
４ｎ2＝900
ｎ2＝225
ｎ＞０より、ｎ＝15
ア…２×15－１＝29
イ…29＋２＝31
＠余談＠
899は900に近い。
30×30＝900で、アとイは連続する２つの奇数だから、
30に近い２つの奇数である〔29×31〕を計算すると899になる。
（２）
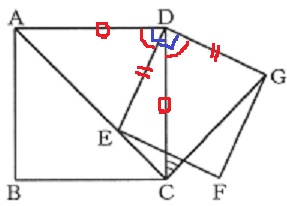
手順どおりに図示。
２つの正方形のそれぞれの１辺。
２つの直角から間の角ＥＤＣをひく。
→２辺と間の角が等しい→合同
ＡＣが正方形の対角線なので、∠ＤＡＥ＝45°
対応する角で、∠ＤＣＧ＝45°となる。
Ⅰ…90
ａ…２辺と間の角
Ⅱ…45
（３）
１～６から２つの数字を選び、それらの積を５で割り、
余りがいくつかでＡ～Ｅが決まる。
全て調査するのが大変。
表を眺めて、なんとなく５で割り切れるところが一番多いような気がする。
１行目…１、２、３、４、０、1
２行目…２、４、１、３、０、２
３行目…３、１、３、２、０、３
４行目…４、３、２、１、０、４
５行目…０、０、０、０、０、０
６行目…１、２、３、４、０、１
試してみると、やはり５が多いが、
試さないと確証が得られないので不安になる(´ﾟдﾟ｀)
余り０はＡで止まるのでア。
四角で囲った数字は11個なので、11/36
（４）Ⅰ
グラフの目盛りに注意しよう！
１マスあたりｘ軸は10分、ｙ軸は400円。
Ｘプランでは、30分を超えると１分あたり＋40円。
10分では＋400円。
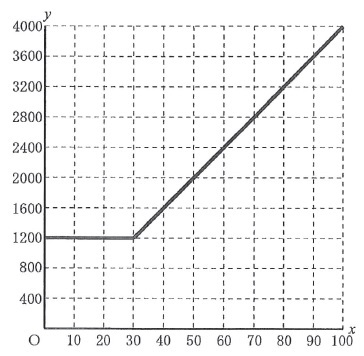
ちょうど、右１上１で増加する。
②
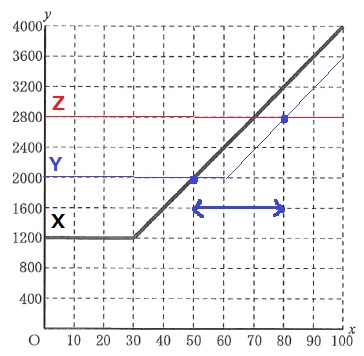
ＹとＺを図示し、Ｙが一番下にくる範囲を探す。
50分から80分までの間。
大問３（図形）
（１）
弧ＣＤの長さから∠ＣＯＤを算出。
360×２π/（５×２×π）＝72°
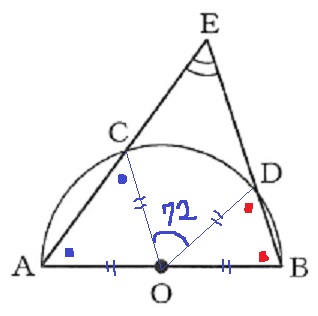
△ＯＡＣと△ＯＢＤは二等辺。
２つの二等辺を一体化させて考える。
∠ＣＯＡ＋∠ＤＯＢ＝180－72＝108
２つの三角形の内角の合計は360°
360－108＝252…●●●●
252÷２＝126…●●
△ＡＢＥで、180－126＝54°
（２）①
中学入試っぽい。
補助線の引き方を知っていれば楽勝だが、初見だと厳しい。
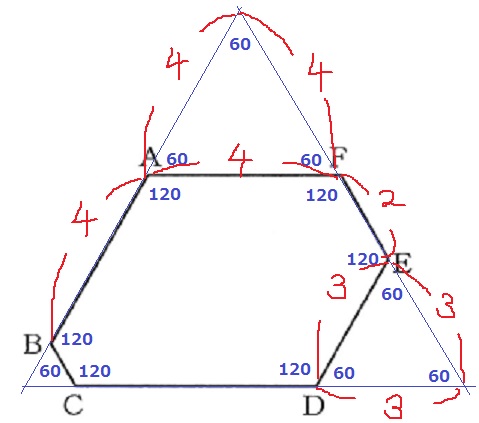
外側に補助線を描くと３つの正三角形ができる。
六角形ＡＢＣＤＥＦは正六角形ではないが、
内角の大きさがすべて等しいので、すべて120度となる。
外側の三角形の２つの内角が60度だから、残りの１つも60度となり、
３つの三角形は正三角形となる。
大きい正三角形の１辺は、４＋２＋３＝９ｃｍ
左下の小さな正三角形の１辺は、９－４－４＝１
ＣＤ＝９－１－３＝５ｃｍ
②
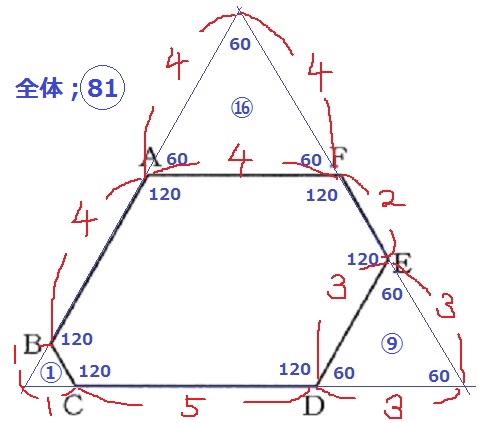
面積比で攻略。
大きな正三角形は⑨×⑨＝○81
外の３つの正三角形は、
④×④＝⑯、①×①＝①、③×③＝⑨
真ん中の六角形は、○81－⑯－①－⑨＝○55
大きい正三角形の底辺は９、高さは９×√３/２
９×９×√３/２×１/２×55/81
＝55√３/４ｃｍ2
（３）①
円Ｏの面積⇒円Ｏの半径がわかればいい。
円外の任意の２つの点から接点までの距離は等しい。
ＢとＤはＡＢ、ＡＤ上で円Ｏが接する接点。
ＡＢ＝ＡＤ＝２
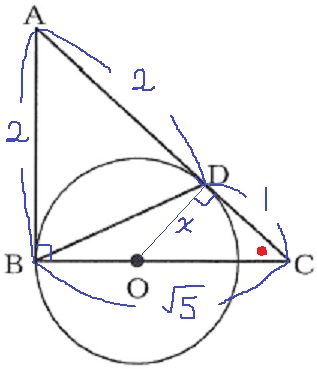
△ＡＢＣで三平方。
ＢＣ＝√５
ＯＤに補助線をひき、ｘとおく。
△ＡＢＣと△ＯＤＣは２角が等しいので相似。
ＣＢ：ＢＡ＝ＣＤ：ＤＯ
√５：２＝１：ｘ
√５ｘ＝２
ｘ＝２√５/５
円Ｏの面積は、（２√５/５）2π＝４π/５ｃｍ2
②
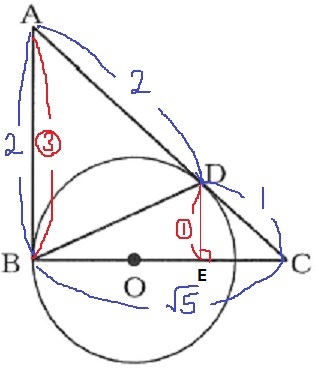
Ｄから垂線をおろし、ＢＣとの交点をＥとおく。
△ＣＤＥ∽△ＣＡＢから、
ＤＥ＝２×１/３＝２/３
△ＤＢＣの回転体は、底辺の半径が２/３、高さが√５の円錐となる。
２/３×２/３×π×√５×１/３＝４√５π/27
円の回転体は、半径２√５/５の球。
球の体積→３/４πｒ3
３/４×（２√５/５）3×π＝32√５π/75
32√５π/75÷４√５π/27＝25/75倍
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
色んな都道府県の過去問を解きながら勉強しているのですが、このページがとてもありがたいです、
一番お世話になってるサイトです????????♀️????????♀️
わからないときはまずここを見に来ます！
コメントありがとうございます。
そう言って頂けて、こちらも大変励みになります。
ときおり、変な解法をかますときがありますので、
違和感のある解説がありましたら他サイトか最寄の数学の先生に尋ねてください（＾＾;
2023年の解説も行う予定ですので、またいらしてください。
サボ