2022年度　愛知県公立高校入試Ｂグループ過去問【数学】解説

合格者平均13.2点（前年比；＋0.3点）
問題はコチラ→ＰＤＦファイル
2022年度・愛知Ａ問題（数学）の解説はコチラ。

大問１（小問集合）

（１）
６÷（－２）－（－７）
＝－３＋７
＝４

（２）
２（６ｘ－８ｙ）＋３（５ｙ－４ｘ）
＝12ｘ－16ｙ＋15ｙ－12ｘ
＝－ｙ

（３）
（ｘ＋５）（ｘ－２）－３（ｘ－３）
＝ｘ²＋３ｘ－10－３ｘ＋９
＝ｘ²－１　←平方の差だから終わりではない!
＝（ｘ＋１）（ｘ－１）

（４）
（√５＋√２）²－（√５－√２）²
＝｛√５＋√２＋（√５－√２）｝｛√５＋√２－（√５－√２）｝
＝２√５×２√２
＝４√10

（５）
（２ｘ＋１）²－３ｘ（ｘ＋３）
＝４ｘ²＋４ｘ＋１－３ｘ²－９ｘ
＝ｘ²－５ｘ＋１＝０
解の公式を適用。
ｘ＝（５±√21）/２

（６）
消しゴムｙ個は、配った３ｘ個より多いから余った。
ｙ＞３ｘ

（７）
６の約数は〔１・２・３・６〕
確率は４/９。

（８）
正方形の１辺は８と６の最小公倍数24ｃｍ。
縦は、24÷８＝３枚
横は、24÷６＝４枚
枚数は、３×４＝12枚

（９）
（－３、－８）⇒（１、４）
右に４、上に12だから、傾きは12/４＝３
（１、４）から右に２、上に６移動して、ｙ＝４＋６＝10

（10）
ア：１³＝１ｃｍ³
イ：２×２×１÷３＝４/３ｃｍ³
ウ：１×１×π×１÷３＝π/３ｃｍ³
エ：0.5×0.5×π×１＝0.25πｃｍ³
π＝3.14…だから、イの４/３（1.33…）が最も大きい。
イ

大問２（小問集合２）

（１）
選択肢の構造より、ア～ウ、エ～カ、キ～ケの中からそれぞれ１つずつ選ぶ。

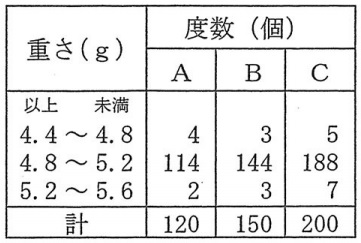
●ア～ウ
合格ネジは114＜144＜188だから、個数でいえばＣが最も多い。

●エ～カ
失敗率の方が大小関係がわかりやすい。
Ａ：６/120、Ｂ：６/150、Ｃ：12/200＝６/100
分子を６で統一すると、分母の大きいＢが最も値が小さい。
つまり、Ｂが最も失敗率が低いから、最も合格ネジの成功率が高い。

●キ～ケ
それぞれの階級値は4.6ｇ、5.0ｇ、5.4ｇ
仮の平均を5.0ｇとおく。
5.0ｇ未満の4.4～4.8ｇの個数と、5.0ｇより大きい5.2～5.6ｇの個数の差を比較する。
Ａ：４－２＝２
Ｂ：３－３＝０
Ｃ：５－７＝－２
仮の平均5.0ｇ未満はＡが最も多い→Ａの実際の平均値は5.0ｇを下回る。
ウ・オ・キ

（２）

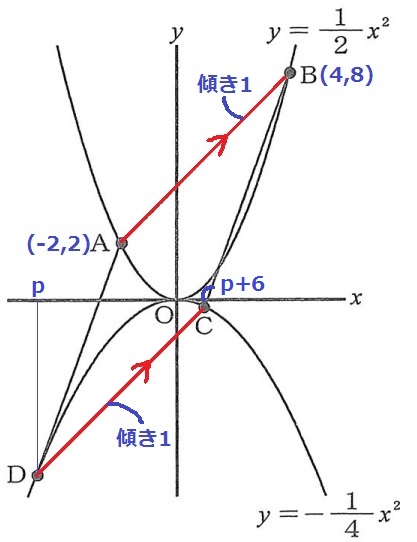
ｙ＝１/２ｘ²にｘ座標を代入。
Ａ（－２、２）→Ｂ（４、８）
右に６、上に６だから、ＡＢの傾きは１。
ＡＢ//ＤＣで、ＤＣの傾きも１。

ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合（＝傾き）はａ（ｐ＋ｑ）
求めたいＤのｘ座標をｐとおくと、Ｃのｘ座標はｐ＋６。
－１/４（ｐ＋ｐ＋６）＝１　←－４倍
２ｐ＋６＝－４
ｐ＝－５
Ｄのｘ座標は－５

（３）①
横軸は秒ではなく、移動した長さ（ｃｍ）である。

最初はＡが入っていく。Ａの横は30ｃｍ。
あいだが30ｃｍで、Ｂが20ｃｍ。
Ａの先端～Ｂの後ろまでの全長は80ｃｍ。
Ｂが完全に荷物検査機に入ったとき、Ａの先端は出口まで残り20ｃｍ。
20ｃｍの横線を描く。

Ａから出ていき、30ｃｍの間隔を空けてＢが出ていく。
点対称のように描けばいい。

②

グラフでもわかるが、100ｃｍの検査機に20ｃｍのＢが完全に入っている長さは80ｃｍ分。
80÷20＝４秒間

大問３（図形）

（１）

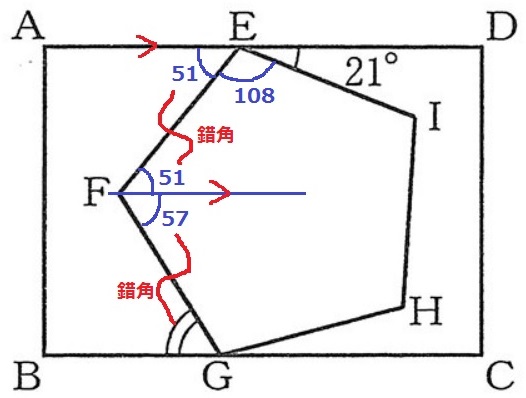
正五角形の１つの内角は108°
∠ＡＥＦ＝180－（108＋21）＝51°

Ｆを通る平行線をひき、51°を下におろす。
108－51＝57°
さらに錯角でおろして∠ＦＧＢ＝57°

＠別解＠
某所で面白い解き方を習得したのでやってみます。

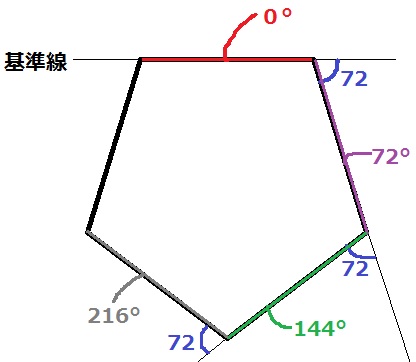
正五角形の１つの外角は72°です。
一番上の辺を基準線とします。
次の辺は基準線を時計回りに72°回転させた直線。
その次は144°、その次は216°回転させた直線です。

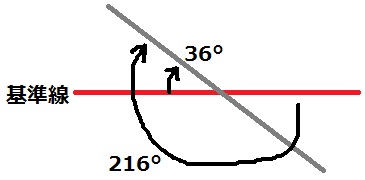
直線は半回転させても姿は変わらないので、
時計回りに216°回転ということは、216－180＝36°の回転と同じです。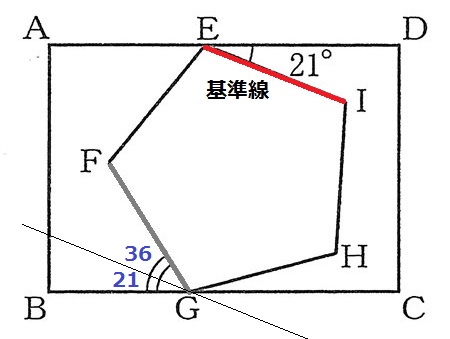
本問では基準線ＥＩがすでに時計回りに21°傾いているので、
∠ＦＧＢ＝36＋21＝57°となります。

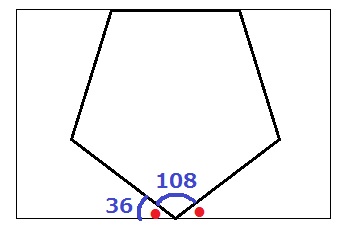
とどのつまり、この状態の正五角形を時計回りに21°動かした感じ。

（２）①

公立入試でいたるところに出てくる。
空間の斜め線はそれを対角線とする直方体を想像する。
【１辺がａ、ｂ、ｃの直方体の対角線の長さは√（ａ²＋ｂ²＋ｃ²）】
ＩＪ＝√（２²＋３²＋６²）＝７ｃｍ

②

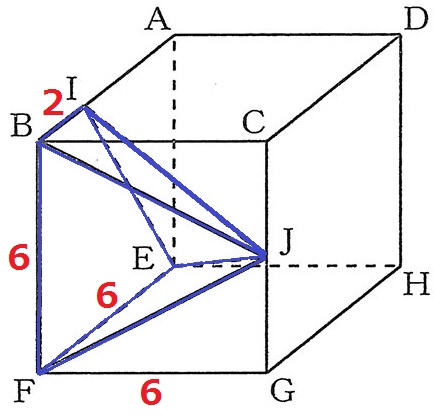
四角錘Ｊ―ＢＩＥＦの体積を求める。
必要な辺の情報は出揃っている。
（２＋６）×６÷２×６÷３＝48ｃｍ³

（３）①

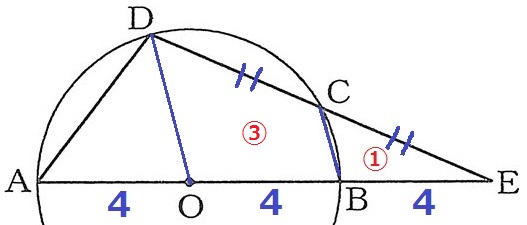
仮定と半径より、ＡＯ＝ＯＢ＝ＢＥ＝４ｃｍ、ＤＣ＝ＣＥ
ＢとＣは、それぞれＯＥとＤＥの中点にある。
中点連結定理から△ＣＢＥ∽△ＤＯＥの相似比は１：２。
△ＣＢＥの面積を①とすると、四角形ＯＢＣＤは④－①＝③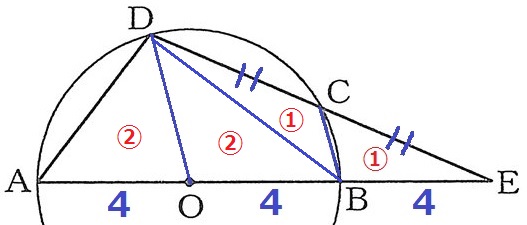
ＢＤに補助線。
ＤＣ＝ＣＥより、△ＤＢＣ＝△ＣＢＥ＝①
△ＤＯＢ＝③－①＝②
ＡＯ＝ＯＢより、△ＤＡＯ＝△ＤＯＢ＝②
△ＣＢＥは四角形ＡＢＣＤの１/５倍。

②
長さが半径４ｃｍしかわかっていない。
有名角も見当たらないので、こういう場合は相似を疑う。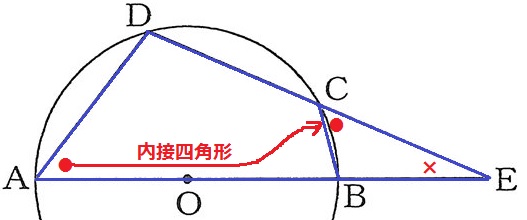
四角形ＡＢＣＤは円に内接している。
円に内接する四角形の内角は、その対角の外角に等しい。
∠ＤＡＥ＝∠ＢＣＥ（●）
これと共通角（×）と合わせて２角相等→△ＡＤＥ∽△ＣＢＥ

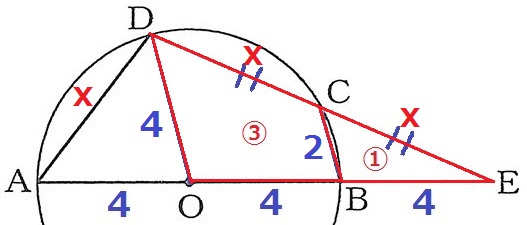
先ほどの中点連結定理で、ＣＢ＝ＤＯ÷２＝２ｃｍ
ＣＢ：ＢＥ＝ＡＤ：ＤＥ＝１：２だから、ＡＤ＝ｘとおくとＤＥ＝２ｘ
ＣＥ＝ｘ

【ＡＤ：ＡＥ＝ＣＢ：ＣＥ】
ｘ：12＝２：ｘ
外項と内項の積より、ｘ²＝24
ｘ＞０だから、ｘ＝２√６
ＡＤの長さは２√６ｃｍ