平均54.0%(前年比;+6.4%)
問題はこちら→リセマムさん
大問1(小問集合)-81.9%
(1) 96.4%
6+3×(-5)
=6-15
=-9
(2) 90.1%
3(a-4b)-(2a+5b)
=3a-12b-2a-5b
=a-17b
(3) 64.1%
(√18+√14)÷√2
=√9+√7
=3+√7
(4) 83.1%
(x-2)(x+2)=x+8
x2-4=x+8
x2-x-12
=(x+3)(x-4)=0
x=-3、4
(5) 87.0%
反比例の比例定数aは積xyで一定。
y=2×9÷(-3)=-6
(6) 81.4%
5枚から2枚を取り出す→5C2=10通り
3を含む組み合わせは、〔3・3以外〕で4通り
確率は4/10=2/5
@余談@
端的に考えて、異なる5枚から選んだ2枚に該当する数字がでてくる確率は2/5
(7) 76.8%
y=1/4x2のグラフを描く。
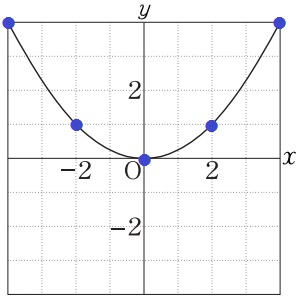
a>0ゆえ、下に凸のグラフになる。
通過すべき格子点を意識しよう。
(-4、4)(-2、1)(0、0)(2、1)(4、4)
(8) 76.0%
累積相対度数は、その階級以下の相対度数の合計。
20m未満の合計は、6+9+17=32
32/60=8/15=0.533…≒0.53
(9) 82.4%
印アリは50個中6個。この割合は母集団も同じとみなす。
30×50/6=250個
大問2(データの活用)-68.7%
(1) 68.3%

ア:AのQ1(第1四分位数)は7点。×
イ:Bの最大値は17点。〇
ウ:AのQ2(中央値)が10点、BのQ1が10点。
15個のQ2は8番目の値、Q1は下位7つの真ん中(下から4番目)の値。
10点以上はBの方が多い。×
エ:範囲(レンジ)=最大値-最小値。Aは18-4=14、Bは17-2=15でBの方が大きい。〇
イ・エ
(2)PQ…89.7%、RS…67.4%、Z…59.2%
中央値はAが10点、Bが12点。
四分位範囲=Q3-Q1。Aが14-7=7点、Bが15-10=5点
P…10、Q…12、R…7、S…5
Z…Bの方が中央値が大きく、四分位範囲は小さい。
*大小関係を記述すればいい。
中央値が大きい→Bの方が好成績が多い
四分位範囲が小さい→極端な値を排除した中央付近に好成績が集中する。
AよりBの方が高いスコアを出す根拠になる。
大問3(方程式)-36.2%
都立大問2と瓜二つ。
(1) 62.6%
左右の半円は足して1つの円で計算する。
A:πr2+2ar
B:πa2+2ar
A-B
=(πr2+2ar)-(πa2+2ar)
=π(r2-a2)
ウ
(2)X…22.2%!、Y…30.4%!、Z…23.3%!
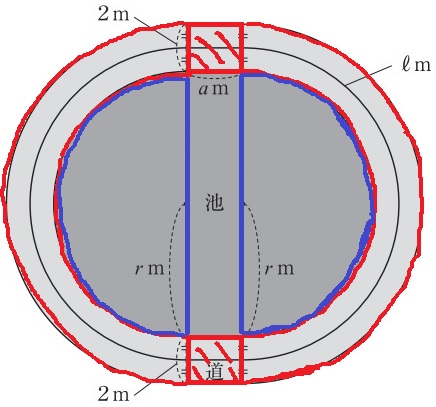
Sは大きな円から小さな円を引き、真ん中は上下の長方形を足す。
S=(r+2)2×π-πr2+2a×2
=(r2+4r+4-r2)π+4a
=4a+4πr+4π
=4(a+πr+π) …①
ℓは直径2r+2の円周とa2つ分。
ℓ=(2r+2)π+2a
=2a+2πr+2π
=2(a+πr+π) …②
①、②より、S=2ℓ
X…4a+4πr+4π、Y…2a+2πr+2π、Z…S=2ℓ
大問4(数量変化)-49.0%
(1) 75.4%
正午~午後1時30分は「中」
1時間で500mL消費する。
90分=3/2時間だから、500×3/2=750mL
(2) 47.9%
2時間後の残りは、4200-500×2=3200mL
「強」は1時間あたり700mL⇒傾きは-700
y=-700x+bに(x、y)=(2、3200)を代入。
3200=-700×2+b
b=4600
(y=)-700x+4600
(3) 36.6%

Bは2~7時の5時間で4000mL消費する。
1時間あたりの変化率は-800mL。

最後の部分をピックアップ。
減少率はA:B=【3】:【8】
同じ減少量に対する時間の比は逆比でA:B=⑧:③
差の⑤が1時間に相当する。
③=1×③/⑤=3/5時間=36分
答えは7時の36分前である午後6時24分
大問5(平面図形)-43.1%
(1) 71.1%
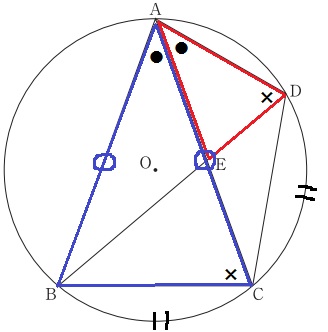
桜がほぼ言っているが、二等辺ABCとの相似を利用して、
△AEDも二等辺であると指摘すれば、AE=ADが証明できる。
答えは△AED(もしくは△ADE)
@余談@
問題では相似の証明は不要だが、弧ABに対する円周角(×)と、
弧BC=弧CDからこれらに対する円周角(●)で2角相等→∽
(2) 59.0%
△ABE≡△ACDの証明。
合同の証明は先に等辺を確認すると方針が立てやすい。
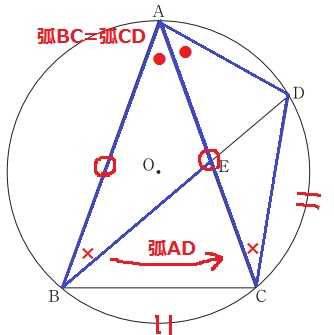
仮定から、AB=AC
弧ADに対する円周角で、∠ABE=∠ACD
弧BC=弧CDより、∠BAE=∠CAD
1辺と両端角が等しいので合同。
(3) 9.2%!!
4cmしかわかっていない。
有名角の30°を手がかりに有名三角形を探す。
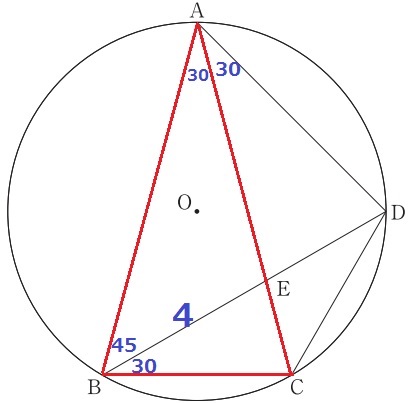
弧BC=弧CDで∠CAD=30°
弧CDに対する円周角で、∠CBD=30°
二等辺ABCの内角より、∠ABE=(180-30)÷2-30=45°
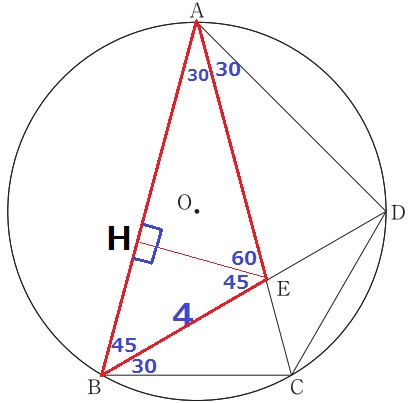
Eから垂線をひき、ABとの交点をHとすると、
△BEHは辺の比が1:1:√2の直角二等辺三角形→EH=2√2cm
△AEHは辺の比が1:2:√3の直角三角形→AE=4√2cm
大問6(空間図形)-20.3%
(1) 67.4%

ア:AB//HGだからHG上のHLも平行。〇
イ:面ADHEは背面。面JKLIは斜面で上に伸ばすと交わる(平行ではない)。×
ウ:∠JBA=∠JBC=90°より、面ABCD⊥辺BJ。〇
エ:DHとKLを延長すると交わる。ネジレではない。×
ア・ウ
(2) 10.7%!
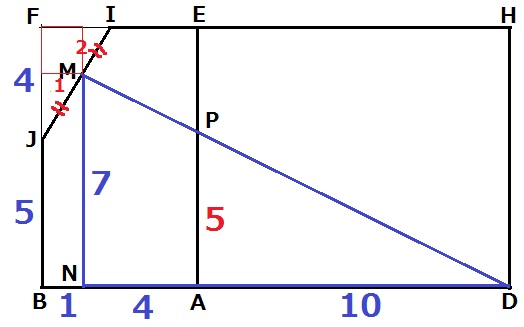
最短距離なので展開図を作成。
Pの位置を探るが、長さの認定がやや大変。
Mの垂線の足をNとする。
MN=9-2=7cm
ND=5-1+10=14cm
△MND∽△PADで、PA=7×10/14=5cm
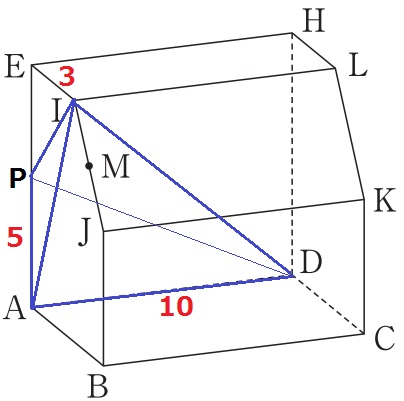
三角錐I—APDの体積は、10×5÷2×3÷3=25cm3
(3) 4.0%!!

△ABJで三平方→直角二等辺の辺の比は1:1:√2で、AJ=5√2cm
△ABCで三平方→AC=5√5cm
△ABC≡△JBCより、JC=5√5cm
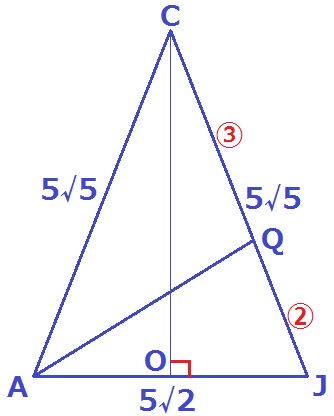
△ACJは二等辺三角形。
Cの垂線の足をOとする。△ACOで三平方。
CO2=(5√5)2-(5√2/2)2
CO=√(125-50/4)
=√(450/4)=15√2/2cm
△ACJの面積を②/⑤倍すれば△AQJである。
5√2×15√2/2÷2×②/⑤=15cm2
@別解@

三角錐C―ABJはAB(BJ):BCの長さの比が1:2。
中学受験に出てくる有名錐で、これを展開すると正方形になる。
△ACJ=10×10-(5×5÷2+5×10÷2×2)=37.5cm2
△AQJの面積は、37.5×②/⑤=15cm2
●講評●
例年通り、バランスよく出題されている。
大問1
(6)5枚のカードのうち、当たりは1枚。2枚選んで当たる確率は2/5。
当たりのカードを3と考えればいい。
(7)格子点のズレがないように!
(8)累積相対度数おぼえていたかな?
大問2
(1)ウ:箱全体が10点以上のBが多い。
(2)基本レベル。記述は2つの要素の大小関係を書けば足りる。
大問3
珍しい形式ではないが、都立そっくり模試みたい。
(1)円+長方形の面積を文字で丁寧に表せるか。
AとBの差は円の差になる。
(2)真ん中は4aを足して省略。共通因数でまとめて整理する。
大問4
(3)解説では中受の戦法を使った。
大問5
(2)△ABEをAを回転の中心として反時計回りに回転移動させると△ACDになる。
(3)30°⇒有名角。角度を調査して、どこに有名三角形があらわれるか。
大問6
(2)長さがまちまちなので、数値を間違えないようにしよう。
(3)△AQJ⇒△ACJ。これを1つの面とする立体は三角錐C―ABJ。
△ABC≡△JBCより、△ACJは二等辺三角形である。



コメント
【訂正が必要です】
大問2(1)
「ウ:四分位範囲が10点以上であるBの方が多い。×」
→Bの四分位範囲は5点です。
「Aの10点以上は少なくとも8回以上ある」
→Aの10点以上は最も多い場合で11回あります。このことと、「Bの10点以上が12回以上」であることを比べて、ウが誤りであることがわかります。
コメントありがとうございます。
問題を確認したうえで、あとで修正を加えます。
ご指摘ありがとうございました。
サボ