問題PDF
2019年度(数学)の本試験はコチラ。
大問1(計算)
(ア)
(-10)+(-7)
=-10-7
=-17 【1】
(イ)
1/6-(-2/7)
=1/6+2/7
=19/42 【4】
(ウ)
-63a2b2÷9a2b
=-7b 【3】
(エ)
72/√6-√54
=12√6-3√6
=9√6 【3】
(オ)
-(x-6)(x-2)+(x-8)2
=-x2+8x-12+x2-16x+64
=-8x+52 【2】
大問2(小問集合)
(ア)
(x+3)2-9(x+7)+26
=x2+6x+9-9x-63+26
=x2-3x-28
=(x+4)(x-7) 【1】
(イ)
7x2-4x-1=0
因数分解ができないので、解の公式を適用。
xの係数が偶数なので、b=2b’が使える。
x=(2±√11)/7 【1】
(ウ)
x=-3のとき、y=9a
x=-1のとき、y=a
(a-9a)/{-1-(-3)}
=-4a=5
a=-5/4 【2】
*y=ax2において、p→qまでの変化の割合はa(p+q)
a(-3-1)=5
a=-5/4
(エ)
一次方程式。
xm歩いて、1200-xm走ったとする。
時間で等式を作成。
x/60+(1200-x)/120=18
2x+1200-x=2160
x=960→960m 【4】
(オ)
√126n=3√14n
3√14nが自然数となる(根号を外す)には、
√14nが平方数になればいい。
nの最小値は14。(√(14×14)=14)
2番目に小さいnは、14×2×2=56
3番目に小さいnは、14×3×3=126
4番目に小さいnは、14×4×4=224 【3】
*14に平方数をかけていく。
(カ)
xとyの度数の合計…36-(1+7+13)=15人
全体の回数の合計…平均2.5回×36人=90回
xとyの回数の合計…90-(0×1+1×7+3×13)=44回
x+y=15
2x+4y=44
上の連立を解いて、x=8、y=7 【2】
大問3(小問集合2)
(ア)
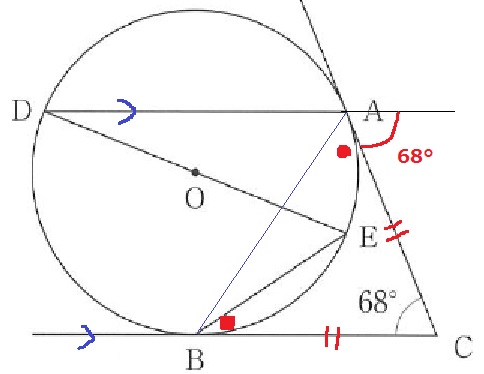
円周角定理から、∠BED=∠BAD
∠BADを求めればいい。
Cから接点A・Bまでの距離は等しい→△ACBは二等辺
∠CAB=(180-68)÷2=56°
68°を錯角で上にあげる。
∠BAD=180-(56+68)=56°
@別解@
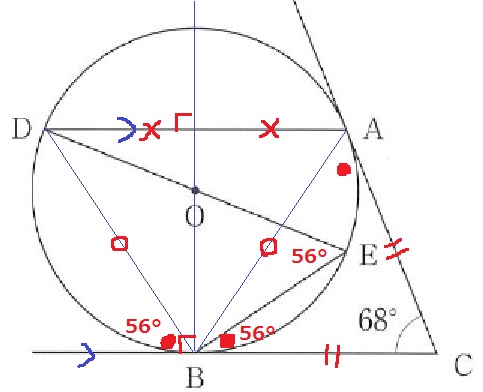
接点Bから垂線を引くと、中心Oを通る。
DA//BCから、OBを対称の軸とする線対称を利用して、
∠ABC=56°を左側に移す。
そこから、弧DBの接弦定理で∠BED=56°
(イ)
数学が得意な子でも厳しいのでは?(( ;゚д゚))
はじめは角度から調査をする。

DOに補助線。△BODは正三角形。
理由は、弧BDに対する中心角BODが360×2/12=60°で、
BO=DO(半径)と組み合わせると、内角がすべて60°になるから。
サボは、うえのように正六角形を6分割した図形で覚えています。
DからBOに垂線、交点をNとするとNO=2
△DNOの1:2:√3から、DN=2√3
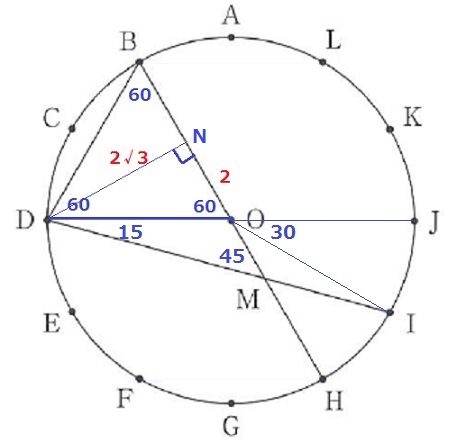
∠MDOを調べる。
∠IOJは360÷12=30°で、∠MDOはこの円周角にあたるから15°
△MDOで外角定理→∠DMO=60-15=45°
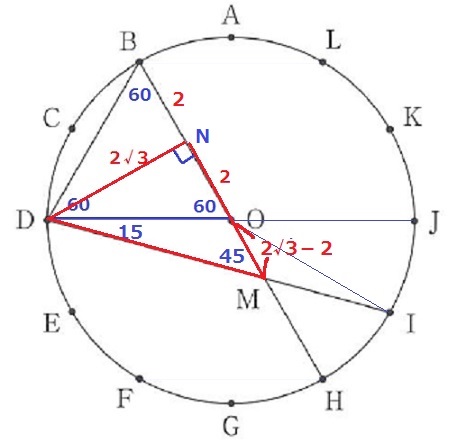
△NMDが90°-45°-45°の直角二等辺三角形!
これに気づかなければならない。
NM=2√3より、OM=2√3-2
△BDMは底辺BM、高さDNだから、
(2+2+2√3-2)×2√3÷2
=6+2√3cm2
*図をパッとみたときに相似かな?と思ったのですが、
半径4cmしか情報が与えられていないので、円周12等分から角度を調査していき、
有名角に気づいて図形の性質をひもといていく。
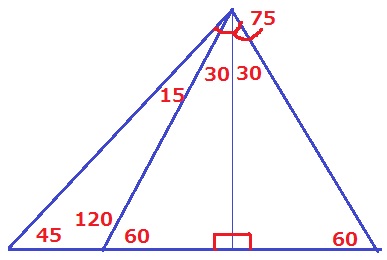
しかし、この有名角は中3でどのくらい知名度があるのか??
内角が45°-75°-60°ときたら、すぐに思い浮かべて使えるようにしておかないと時間オーバー。
*上記の解法以外で解けました方は、ぜひお問い合わせよりお知らせ願います。
(ウ)
整数の証明。
中央の数をxとする。連続する3つの奇数はx-2、x、x+2
ⅰ:8(x-2)+5(x+2)=x2+30
ⅱ:上の式を解く。
x2-13x-36=(x-4)(x-9)=0
xは奇数なので、x=9
大問4(関数)
(ア)
Aのx座標は-6なので、これをy=-3/2xに放り込む。
A(-6、9)
これをy=ax2に放り込む。
9=(-6)2a
a=1/4 【2】
(イ)
y=8/xから、E(8、1)
F座標が知りたい。
ここでAO:OF=4:1を使う。
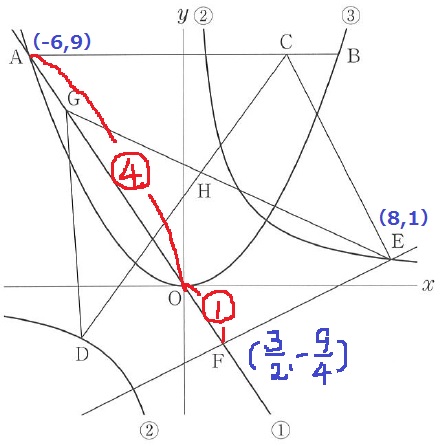
Aのx座標とy座標を÷4する。符号に気をつけること!
Fは第四象限(左下)なので、x座標は正、y座標は負となる。
F(6÷4、-9÷4)=(3/2、-9/4)
2点を通る式→連立方程式
1=8m+n
-9/4=3/2m+n
毎度のごとく数字が汚いが、これを解いて、
m=1/2、n=-3
ⅰ:【5】、ⅱ:【6】
(ウ)
△CHEと△DHGの面積が等しい。
結論から申し上げますと、DE//GC
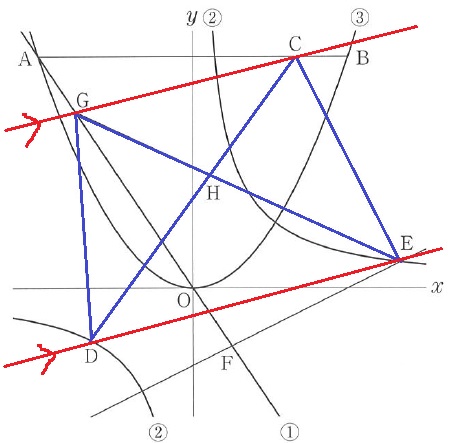
△CHEと△DHG、それぞれに△DHEを足してみよう。
共通部分である△DHEを足した、△CDEと△GEDも面積が等しくなる。
2つは底辺DEが共通するので、高さも等しいはず。
ここでお馴染みの等積変形を用いる。
DEとGCを引くと高さが共通であることから、2本の直線が平行となる。
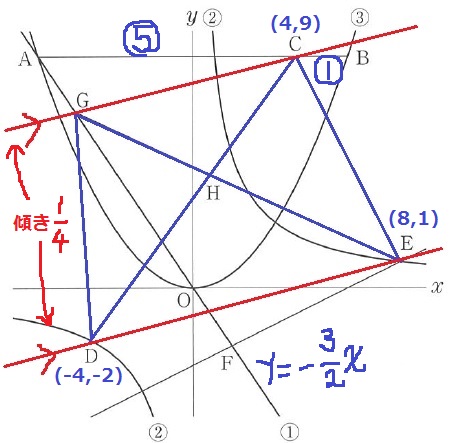
D(-4、-2)→E(8、1)
右に12、上に3なので、DEの傾きは3/12=1/4
AC:CB=5:1より、C座標は(4、9)
9=4×1/4+b
切片b=8
GC;y=1/4x+8
Gは、y=-3/2xとy=1/4+8の交点。
-3/2x=1/4x+8
x=-32/7
y=-32/7×(-3/2)=48/7
G(-32/7、48/7)
大問5(確率)
(ア)
点同士の距離が整数→間の数が30の約数。
30÷1、30÷2、30÷3、30÷5、30÷6、30÷10
間の数が【1・2・3・5・6・10】個になればいい。
注意点は、間の数はa+b(PQ内部の点の数)に+1されること!
つまり、間の数から-1した数がa+bの和になる。
a+bの和で0と1は不適なので、【2・4・5・9】のどれか。
・a+b=2→(1、1)
・a+b=4→(1、3)×2、(2、2)
・a+b=5→(1、4)×2、(2、3)×2
・a+b=9→(3、6)×2、(4、5)×2
計12通り。
12/36=1/3 【4】
(イ)
厳しい。
aとbの距離が9cm以上を探す。
aとbの和で目盛りの長さ(点同士の距離)が決まり、aとbの差が目盛りの数となる。
aとbが9cm以上離れているより、9cm未満に接近している場合を考え、
あとで全体からひく手法をとる。
◆aとbが重なる。
すなわち、aとbが同じ出目のとき。
たとえば、(2、2)が出たとすると、間の数は5個となり、
目盛りの長さは30÷5=6cmとなるが、aとbは同じ場所にいるので、
互いの距離は0cm→9cm未満の距離となる。
1~6まで6通り。
◆aとbが1目盛り違い。
目盛りの大きさは、30/(a+b+1)
30/(a+b+1)<9
30<9(a+b)+9
9(a+b)>21
a+b>21/9=2・1/3
aとbは整数だから、a+bが3以上になればいい。
つまり、aとbの和が3以上で、かつaとbが1つ違いを調べる。
(1、2)(2、3)(3、4)(4、5)(5、6)
これらの逆を含めて10通り。
◆aとbが2目盛り違い。
30/(a+b+1)×2<9
a+b>51/9=5・2/3
aとbの和が6以上で、かつaとbが2つ違いを調べる。
(2、4)(3、5)(4、6)
これらの逆を含めて6通り。
◆aとbが3目盛り違い。
30/(a+b+1)×3<9
a+b>9
aとbの和が10以上で、かつaとbが3つ違いを探すが、
3つ違いは最大で(3、6)と和が9なのでゼロ。
よって、9cm未満の場合は全部で22通り
9cm以上の場合は、36-22=14通り
確率は14/36=7/18
*おそらく、多くの生徒は正解できないと思われる。
まず題意をくみとれないとオワリです。(1)だけ頑張って(2)はスキップした方がいい。
大問6(空間図形)
(ア)
高さがわかっているので、底面積ABCDの面積が知りたい。

等脚台形は他の都道府県でもよくでてくるので、扱いに慣れておこう。
補助線を2本ひき、上底を下底へ移す。左右対称から両サイドが1cm。
台形の高さは三平方→√(22-12)=√3cm(1:2:√3)
よって、四角錐の体積は、(2+4)×√3÷2×2÷3=2√3cm3 【3】
(イ)
ここからすでにムズイと思うんですけど(;`ω´)
まず、△ACGの1辺である辺ACの長さを求める。
先ほどの等脚台形の高さを出すときに、1:2:√3の直角三角形があった。
ということは、等脚台形の下の角は60°となる。
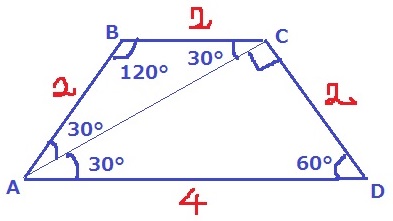
∠BAD=60°から、∠ABC=120°
△ABCは二等辺→2つの底角が30°
ここから、△ACDが30°-60°-90°、すなわち、1:2:√3の直角三角形になる。
AC=2×√3/1=2√3cm

等脚台形にADの中点Fを追加。
角度や周りの2cmをもとに考えていくと、3つの正三角形がみつかる。
BF=CF=2cm
右の立体図に戻る。
△AEFで三平方→AE=2√2
AF=BF=CF=DF=2cmから、
2辺とあいだの直角が等しく、△AEF≡△BEF≡△CEF≡△DEF
(EFを回転の軸として△AEFを反時計回りにまわす感じ)
EC=2√2cm→△EACは二等辺三角形
GはECの中点なので、求積すべき△ACGは△EACの面積の半分となる。
△EACは2√2、2√2、2√3の二等辺。
高さは三平方→√5cm
よって、2√3×√5÷2÷2=√15/2cm2 【2】
(ウ)
余弦定理だろこれ(#゚Д゚)
中3と高3間違えたんだね(*’ω’*)w
AHの長さなので、展開図をつくる。
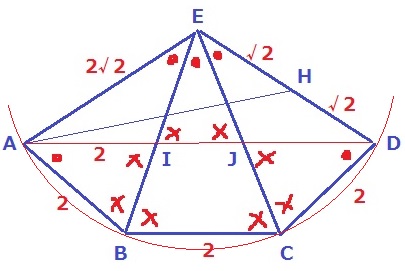
前問で述べた通り、3つの二等辺は合同。
EからA・B・C・Dが等距離にあるので、弧を描いてみると、
∠BADは、弧BDに対する中心角BED●●の円周角にあたるので●となる。
二等辺三角形EABの内角を●-×-×とおくと、△AIBと△DJCも●-×-×となる。
二等辺なので、AB=AI=DC=DJ=2
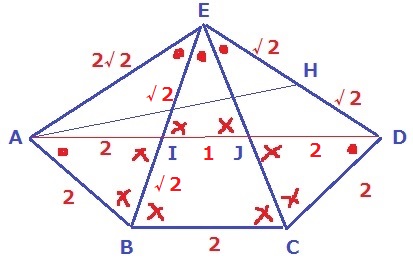
△EAB∽△AIBから、BI=2×2/2√2=√2
ここからI・JはEB・ECの中点であるとわかる。
△EBC∽△EIJより、IJ=1
AD=2+1+2=5
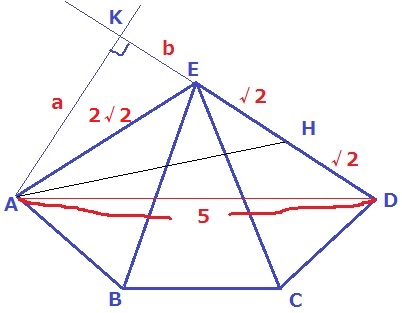
DEの延長線とAから垂線をおろした交点をKとする。
AK=a、KE=bとおく。
△AKEで三平方→a2+b2=(2√2)2 …①
△AKDで三平方→a2+(b+2√2)2=52 …②
a2+b2=8 …①’
a2+b2+4√2b=17 …②’
①’-②’…4√2b=9
b=9√2/8
①’に代入。
a=5√14/8
△AKHで三平方。
AH2=(5√14/8)2+(9√2/8+√2)2
=√(350+578)/64=√928/64=√58/2cm
*最後の三平方の計算はえげつないよ!
これよりベストな解法を編み出した方は、ぜひお問い合わせよりお知らせ願いますm(_ _)m
いつも思うのだが、こういうのを公立高校入試に平然と出してくる累犯加重の県教育委員会の方針に、
納得している神奈川の教職員や塾講師、家庭教師はどんだけいるのだろうか?素朴なギモン
@別解@
お問い合わせよりJohnさん、コメントより匿名さんから素敵な解法を頂きました。

EからBC、HからADに垂線を引き、それぞれの交点をK、Lとし、
EKとADの交点をMとします。
△EBKで三平方→EK=√7cm
前出の相似からMはEKの中点なので、EM=√7/2cm
△EMD∽△HLD(中点連結定理)から、HL=√7/4cm
AD=5cmなので、AL=5×3/4=15/4cm
最後に△ALHで三平方→AH=√58/2cm
大問7(平面図形)
(ア)
誘導に従う。
i:
うしろに∠BAD=∠BFDとあり、
この2角はともに弧BDに対する円周角。
ⅱ:
等しい角に●をする。
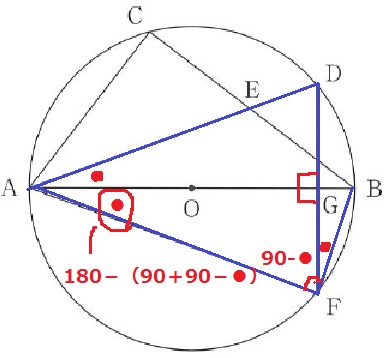
∠FAGは、△AFGの内角から、180-(90+90-●)=●となり、
∠DAG=∠FAGが導ける。 【6】
*∠DAG=∠BFG…③
∠AFG=90°-∠BFG…⑤
∠FAG=90°-∠AFG…⑥
並べてみると、鎖のチェーンのようにつながっている。
ⅲ:
直角と等しい角●と共通辺AG
→一辺両端角相等
(イ)
最後は適度にちょうど良い問題。
角度を調査していくと、30°-60°-90°の直角三角形が複数みつかる。
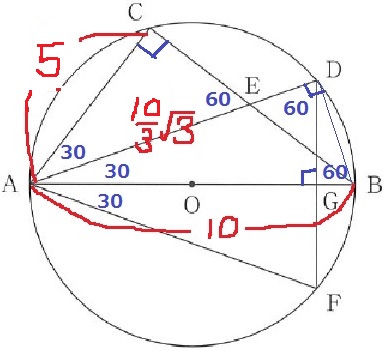
1:2:√3をフル活用。
△ABC→AC=10×1/2=5
△ACE→AE=5×2/√3=10√3/3
△ABD→AD=10×√3/2=5√3
DE=AD-AE=5√3-10√3/3=5√3/3cm
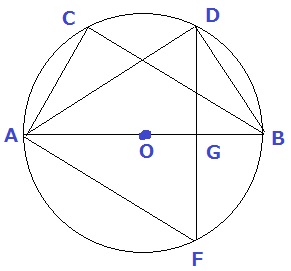
正しく作図すると、こんな感じになる。
今までの設問をいくつか無視してここまでたどり着ければ正解できると思う。
2019年度(神奈川)
数学…平均50.3点 社会…平均42.3点 理科…平均61.3点 英語…平均49.8点
その他は下記リンクの目次からどうぞです。



コメント
いつもありがとうございます。
今更ながら解いてみました。
問6の(ウ)ですが、HからADに垂線をひき、三平方をするととんでもない数は出てこないかな、と思いました。
神奈川県は、どんな能力をつけさせたいのですかね・・。
コメントありがとうございます。
その解法は気づきませんでした。外側より中が良かったですね(^^;
奇しくも匿名さんと同じ解法を2日前にお問い合わせより頂きまして、
別解として付記してよろしいでしょうかとメールを送り、まだ返信がきていないのですが、
匿名さんのコメントをきっかけにのちほど記事に付記させて頂こうと思います。
他に気づいたことがありましたら気兼ねなくコメントしてください。
@@
神奈川数学の荒々しさはミステリーですね‥。
サボ