平均26.5点(前年比;+0.4点)

問題はこちら→リセマムさん
大問1(計算)
(1) 97%
-3-6
=-9
(2) 78%
(2x-5y)/3+(x+3y)/2
={2(2x-5y)+3(x+3y)}/6
=(4x-10y+3x+9y)/6
=(7x-y)/6
(3) 83%
(3x2y-2xy2)÷xy ←分配法則
=3x2y÷xy-2xy2÷xy
=3x-2y
(4) 57%
√10/√2-(√5-2)2
=√5-(9-4√5)
=√5-9+4√5
=5√5-9
(5) 77%
(a-3)(a+3)+(a+4)(a+6)
=a2-9+a2+10a+24
=2a2+10a+15
大問2(小問集合)
(1) 58%
5x2+4x-1=0
解の公式を適用。xの係数が偶数だからb=2b’が使える。
x=(-2±3)/5=1/5、-1
(2) 88%

3本目の平行線をひいて錯角。
x=110-35=75°
(3) 71%
ア:最頻値(モード)は最もあらわれている値で、Aは6.5時間、Bは7.5時間。×
イ:Aは7/30、Bは21/90で等しい。×
ウ:13÷30≒43%×
エ:90人の中央値(メジアン)は45番目と46番目の平均、7~8時間の階級に含まれる。×
イ
(4) 69%
6個から2個を選ぶ→6C2=15通り
赤1個と白1個を取り出す→4C1×2C1=8通り
確率は8/15
(5) 62%
3×3×π×10=90πcm3
(6) 50%
ABを1辺とする正方形の作図。
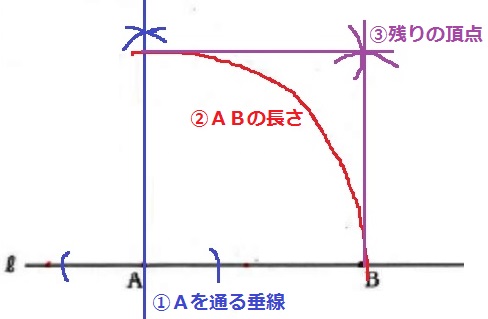
①Aを通る直線ℓの垂線。
②ABの長さをとり、①の垂線との交点が正方形の頂点。
③ABの長さを維持して右上の頂点をつくる。
(7) 42%
答案では求める過程も書く。
求めたい9月の男子をx人、女子をy人とする。
1つ目は、9月の利用者数で立式。
x+y=253-33 …①
2つ目は、増加した人数で立式。
0.21x+0.1y=33 …②
②×10-①で、1.1x=110
x=100
これを①に代入して、y=120
9月の男子は100人、女子は120人
大問3(整数)
(1) 80%
Qは最大数と最小数の差。
Q=762-267=495
ア…495
(2)イ…70%、ウ…57%
最大数…100a+10b+c、最小数…100c+10b+a
Q=(100a+10b+c)-(100c+10b+a)
=99a-99c=99(a-c)
a-cは整数だから、Qは99の倍数である。
イ…100c+10b+a、ウ…99
(3)① 4%!!
先ほどの解答から、aとcの組み合わせを絞る。
Q=99(a-c)=396
a-c=4
a>cだから、(a、c)=(9、5)(8、4)(7、3)(6、2)(5、1)の5通り
ここから、bをあいだに挿入する。
a>b>cなので、bはおのおの3通りずつある。
(たとえば、a=9、c=5であれば、b=6~8の3通り
a=8、c=4であれば、b=5~7の3通り)
3×5=15通り
② 18%!
9≧a>b>c≧1で、Q=99(a-c)
Qの値はaとcの差に依存する。
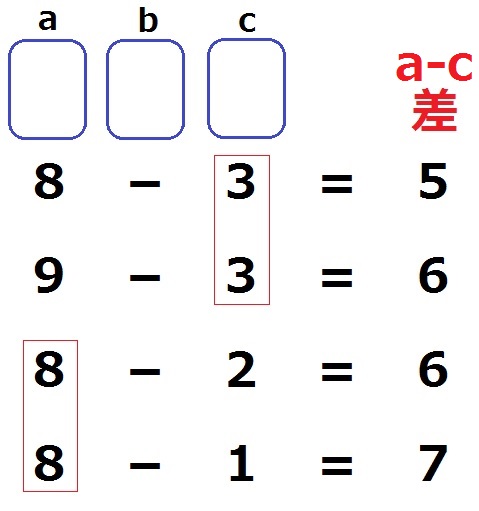
a~cには3と8が含まれる。
c=3で固定すると、aは8・9しかない。
a=8で固定すると、c=3・2・1しかない。
差をとると、a-c=5・6・7
Q=99(a-c)なので、
99×5=495
99×6=594
99×7=693
Q=495、594、693
大問4(数量変化)
(1) 67%

DAとRQの交点をEとする。
△PQR∽△AQEから、△AQEは直角二等辺三角形。
AE=AQ=3cm
y=3×3÷2=9/2
(2)① 55%
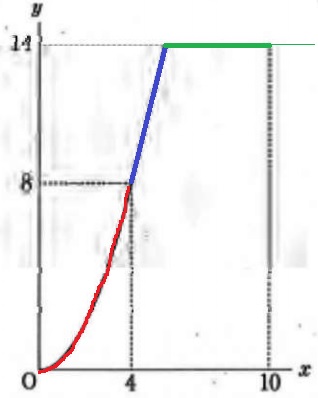
グラフに注意!
0≦x≦4の赤が放物線、青が一次関数で直線、緑はy=14
y=ax2に(x、y)=(4、8)を代入。
8=16a
a=1/2
y=1/2x2
②a…27%!、b…6%!!
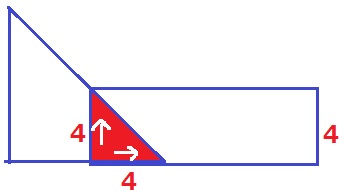
0≦x≦4では、直角二等辺の底辺と高さが伸びるのでy=ax2で増加する。
グラフの転換点であるx=4のとき、最も大きい直角二等辺三角形になる。
aは長方形の縦だから4cm。
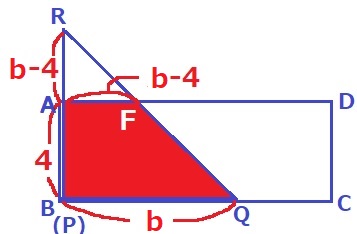
x≧4は重なり部分が台形になる。
高さは4cmで一定、上底と下底が伸びるので一次関数で増加する。
PがBに接したときから重なり部分の形は変わらなくなり、このときの面積が14cm2である。
ADとRQの交点をFとする。
AF=RA=RB-AB=b-4cm
y=(b-4+b)×4÷2=14
b=11/2
a=4、b=11/2
大問5(平面図形)
(1) 23%!
△ABC∽△BDCの証明。

半円の弧に対する円周角は90°
●+×=90°で角度を調査。2角が等しいので∽
(2)① 32%!

前問の△ABC∽△BDCを用いる。
求めるべきBCをxとすると、
AC:CB=BC:CD
3:x=x:1
内項と外項の積で、x2=3
x>0、x=√3
BC=√3cm
② 3%!!

△BDCに着目すると、DC:CB=1:√3の直角三角形。
△BCDは辺の長さは1:2:√3で、内角は30°ー60°ー90°
これと相似関係にある△ABCも△ADBも同様である。
方針【求積すべき図形=△ABD-(△AOC+扇形OBC)】
AB=2√3cm
△ABD…2√3×2÷2=2√3cm2
AO:OB=1:1から、△AOCの面積は△ABCの半分。
△ABCは底辺AC、高さBCで捉え、△AOC…3×√3÷2÷2=3√3/4cm2
∠CBA=60°
△OBCは半径から二等辺三角形→底角60°だから3つの角がすべて60°で正三角形。
∠COB=60°
扇形OBC…√3×√3×π×1/6=π/2cm2
2√3-(3√3/4+π/2)=5√3/4-π/2cm2
●講評●
大問1
(3)分配法則です。
大問2
ここまではなるべく失点をおさえたい。
(6)垂線と長さの写しで正方形は描ける。
(7)9月の利用者は253-33=220人と、すぐ出せるのに気づくこと。
大問3
高得点を目指すなら、問題文はなるべく早く読み切る。
(3)差がつくところであった。
①今年の愛知Aグループ大問2(2)で同じ問題が出されている。
②あいだのbはQに影響しない。
(a、c)=(8、3)の組み合わせ以外は、aは8以上、cは3以下しかない。
大問4
(2)①放物線は途中でまっすぐになる。
②グラフの転換点の様子を作図してみよう。
大問5
(2)①シンプルな構図でみえやすい。
直角三角形の∽は頻出。求めたい長さをxとおいて方程式を立てる。
②弧BCとなる扇形を作成。
角度は有名図形を疑う。直角以外は辺の情報しかない⇒1:2:√3⇒30°―60°―90°!




コメント