平均26.7点(前年比;+2.3点)

問題はこちら→リセマムさん
大問1(小問集合)
(1)① 86.3%
8-6÷(-2)
=8+3
=11
② 81.7%
√27-6/√3
=3√3-2√3
=√3
③ 64.6%
(3x+y)/2-(2x-5y)/3
={3(3x+y)-2(2x-5y)}/6
=(9x+3y-4x+10y)/6
=(5x+13y)/6
④ 70.3%
3ab2×(-4a2)÷6b
=-2a3b
(2) 60.0%
ax2-9a
=a(x2-9)
=a(x+3)(x-3)
(3) 82.9%
x+y=13 …①
3x-2y=9 …②
①×2+②で解くと、
x=7、y=6
(4) 76.0%
2x2-5x+1=0
解の公式を適用して、x=(5±√17)/4
(5) 77.1%
6x=3 …①
x=1/2 …②
①の両辺を÷6して②になる。
エ
(6) 60.6%
不等式の説明問題。
大人1人がa円、子供1人がb円だから、
4a+5b≦7000は大人4人、子供5人の入園料の合計が7000円以下であることを示す。
(7) 72.6%
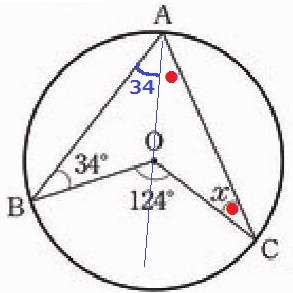
外角定理を用いる。
ブーメランの3つの角の和は股の角。
2(34+●)=124
●=28°
(8) 30.3%!
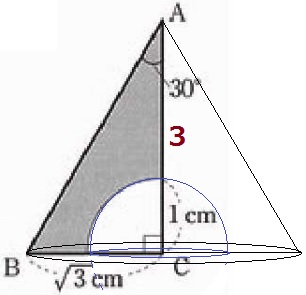
三角錐から半球をひく。
球の体積V=4/3πr3
△ABCの辺の比は1:2:√3→AC=3cm
√3×√3×π×3÷3-4/3π×13÷2
=7/3πcm3
(9) 62.9%
y=-3x+5について正しいものを選ぶ。
ア:x=-3を代入するとy=14。×
イ:原点を通る比例ではない。×
ウ:x=1のときy=2、x=2のときy=-1
1≦x≦2のとき、-1≦y≦2。〇
エ:xの増加量は3-1=2。yの増加量は傾き(変化の割合)の-3をかけて-6。×
ウ
(10) 58.9%
全体は、6×6=36通り
整数になる⇒根号が外れる⇒a+bが平方数。
●a+b=1
無い。
●a+b=4
(1、3)(2、2)(3、1)
●a+b=9
(3、6)(4、5)(5、4)(6、3)
和の最大は12なので、これ以上は無い。
計7通り、確率は7/36
(11) 63.4%(部分正答13.1%)
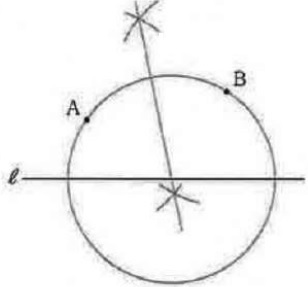
A、Bを通る→円の中心はAとBから等距離にある→ABの垂直二等分線。
これと直線ℓとの交点が円の中心。中心とAの長さが半径である。
(12)①…78.9%、②…78.9%、③…72.6%
△ABD≡△ACEの証明。
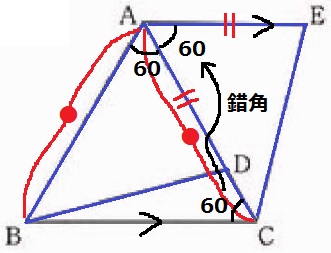
仮定より、AD=AE
△ABCは正三角形だから、AB=AC
∠BAD=∠ACB=60°
AE//BCの錯角より、∠CAE=60°
2辺とその間の角が等しいから合同となる。
△ABD≡△ACEから、対応する辺であるBD=CEが導ける。
ア・ウは正三角形から導ける。合同の証明から『新たにわかること』ではない。
エは成り立たない。
①…オ、②…2辺とその間の角、③…イ
大問2(データの活用)
(1)① 96.6%
a=35-(4+6+7+6+4)=8
30~32gが8個なのはエ
② 44.0%(部分正答13.7%)
答案では相対度数の値を用いてどう推定したかを説明する。
28~30gの相対度数は、7÷35=1/5=0.2
母集団が400個なので、400×0.2=80個と推定する。
(2)b…65.7%、c…68.0%
b+c=35-(2+6+6+4)=17
最頻値が29⇒28~30gのbは7以上、かつCよりも大きい値。
中央値が30~32g⇒(35+1)÷2=18番目が30~32gの階級にある。
b+c=17、b>cの条件から、(b、c)=(9、8)(10、7)(11、6)…
このうち、中央値の条件に適合するのは、(b、c)=(9、8)しかない。
(bが10以上になると、中央値は28~30gの階級に移ってしまう)
b=9、c=8
(3) 25.7%!(部分正答53.7%)
ア:平均を×印などで示す場合もあるが、本問の箱ひげ図にはないのでわからない。×
イ:箱の左端がQ1(第1四分位数)、箱の右端がQ3(第3四分位数)でEが最も大きい。〇

ウ:Q3は300~301番目の平均。Cの34g以上は100個以下だが、
Dの赤い領域に個数が集中しているかもしれないのでEが最も多いとは限らない。×
エ:四分位範囲=Q3-Q1。箱の長さでDが一番大きい。×
オ:Cの30gは上位100個のどこか。(最大でも100個)
DとEの30gはQ2(中央値)未満だから、30g以上は200個以上ある。〇
イ・オ
大問3(規則)
(1)① 58.3%
横…5×3-1×2=13cm
縦…5×2-1×1=9cm
Qの面積は、13×9=117cm3
② 61.7%
Pの横の長さは、5×6-1×5=25cm
面積は5×25=125cm2で、Pの方が大きい。
周の長さは、P…(5+25)×2=60cm
Q…(13+9)×2=44cm、Pの方が長い。
ア
(2) 33.7%
縦の長さ…5×3-1×2=13cm
横の長さ…377÷13=29cm
これをaで表すと、5a-1(a-1)=4a+1
横の長さで立式→4a+1=29
a=7
(3) 12.0%!
3600=60×60
正方形の1辺は最大で60cm。
1辺の長さをbで表すと、5b-1(b-1)=4b+1
4b+1≦60
b≦14.75
bは最も大きい整数だから14
大問4(関数)
(1) 83.4%
y=1/2x2にx=-2を代入して、y=2
(2) 65.7%
A(-2、2)⇒B(4、8)
右に6、上に6だから傾きは1
切片はAから右に2、上に2移動して、2+2=4
y=x+4
(3) 51.7%(部分正答1.1%)
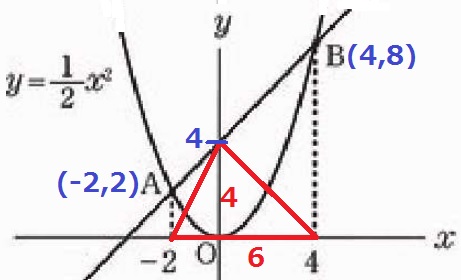
△OABは幅6、高さ4だから、6×4÷2=12
(4)① 34.3%
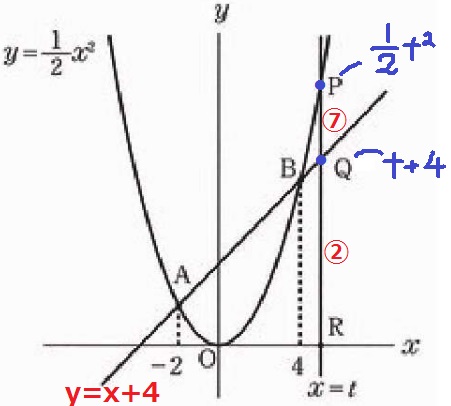
PQの長さは、x=tのときのy座標の差にあたる。
Pはy=1/2x2上の点→1/2t2
Qはy=x+4上の点→t+4
PQ=1/2t2-(t+4)=1/2t2-t-4
② 15.4%!
PQ:QR
=(1/2t2-t-4):(t+4)=⑦:②
外項と内項の積で、2(1/2t2-t-4)=7(t+4)
t2-9t-36
=(t-12)(t+3)=0
t>4より、t=12
大問5(平面図形)
(1) 52.0%
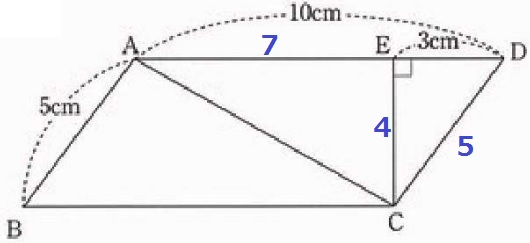
平行四辺形の対辺は等しい。DC=5cm
△CDEは辺の比が3:4:5の直角三角形→EC=4cm
△ACEの面積は、7×4÷2=14cm2
(2)① 22.3%!
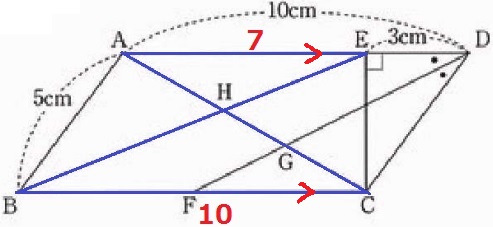
平行四辺形の対辺で、BC=10cm
2角相等(対頂角や錯角)で△AHE∽△CHB
AH:HC=AE:CB=7:10
② 1.7%!!
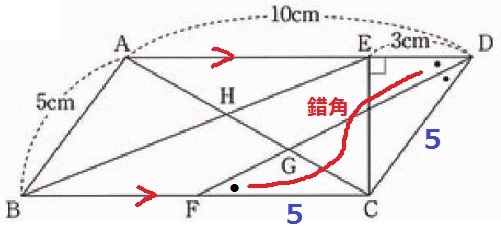
AD//BCの錯角で、∠DFC=●
△CDFは2つの底角が等しいから二等辺三角形。
FC=5cm
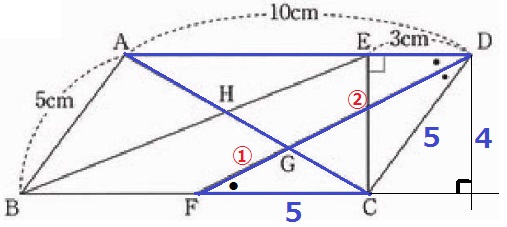
△AGD∽△CGFより、FG:GD=5:10=①:②
方針;【△CDF⇒△CGF】
△CGFの面積は、5×4÷2×①/③=10/3cm2
③ 3.4%!!
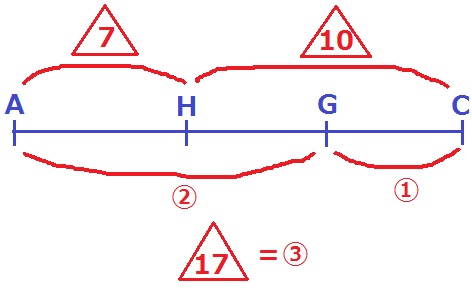
すでに材料はそろっている。
(2)①より、AH:HC=7:10
②より、AG:GC=DG:GF=2:1
△17=③
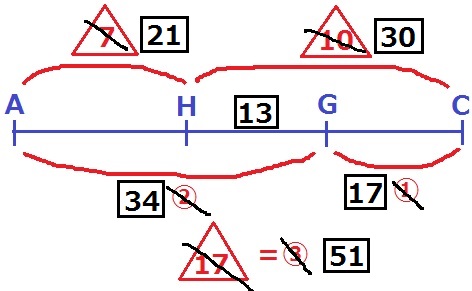
連比で比の合成。
最小公倍数51で合成すると、AH:HG:GC=21:13:17
●講評●
大問1
(2)とりあえずaでくくる。
(6)4aと5bが表すことを書き、その和が7000円以下。
(8)半球は球の半分。球の体積と表面積の公式を忘れずに!
(9)迷ったらグラフを書いた方がいい。
(10)12以下の平方数は3個しかない。
大問2
(1)②相対度数は小数の記述が多い。相対度数は全体を1としたときの割合。
(2)条件を整理する。
(3)他県よりやや難しかった。消去法で絞ってもOK。
大問3
とりやすいところだと思うが全体的に正答率が悲しい(´・_・`)
のりしろの数は〔紙の枚数-1〕個。頻出の形式である。
(1)②周の長さは縦+横の和だけでも比較できる。
(2)そんなに難しくないよ!
(3)解説では一次不等式を解いたが、等式に置き換えて考えればいい。
大問4
ここも典型題。落とすのはもったいない。
(4)おのおののy座標がすぐでる。計算も複雑ではない。
大問5
(2)①時間切れか息切れでしょうか…。頻出の相似形!!
②等角を利用する。△CDFは二等辺で、底辺5、高さ4と確定。
③前問より正答率がやや上がったのは、典型的な手法だからか。
平面のラス問としては易しい部類にはいる。



コメント