2020年度　奈良県公立高校入試過去問【数学】解説

平均25.4点（50点満点、前年比；－1.8点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－74.6％

（１）①　99.3％
５－８＝－３

②　96.1％
－４×（－３）²
＝－４×９＝－36

③　78.0％
（４ａ³ｂ＋６ａｂ²）÷２ａｂ
＝４ａ³ｂ÷２ａｂ＋６ａｂ²÷２ａｂ　←分配法則
＝２ａ²＋３ｂ

④　91.0％
（ｘ＋ｙ）²－５ｘｙ
＝ｘ²＋２ｘｙ＋ｙ²－５ｘｙ
＝ｘ²－３ｘｙ＋ｙ²

（２）　63.2％
絶対値が４より小さい→４は含まない！
－３・－２・－１・０・１・２・３
７個

（３）　86.6％
ｘ²＋５ｘ＋２＝０
因数分解できないので解の公式を適用。
ｘ＝（－５±√17）/２

（４）　84.1％
ｘとｙの積が12で一定→ｙ＝12/ａ
Ａ＝12÷（－２）＝－６

（５）　71.1％
円錐の側面積にあたる扇形の中心角…【360°×半径/母線】
ｘ＝360×５/12＝150°

（６）　43.7％
ア：５÷31＝0.161…〇
イ：階級の幅は2.0℃。×
12.0℃は最大値36.0℃と最小値24.0℃の差で範囲（レンジ）にあたる。
ウ：28.0℃以上は５＋７＋５＋５＝22日×
エ：最頻値（モード）は26.0～28.0の階級値である27.0℃。〇
オ：30.0℃～32.0℃の階級値は31.0℃。×
ア・エ

（７）①　82.8％
５個の玉から２個を取り出す組み合わせ→₅Ｃ₂＝10通り
奇数は３個、偶数は２個。それぞれから１つずつ取り出す→３×２＝６通り
ｐ＝６/10＝３/５

②　79.7％
５個の玉から２個を取り出す。
赤玉は３個、白玉２個。それぞれから１つずつ取り出す。
先ほどと一緒。
よって、ｐとｑは同じ値となる。ウ

（８）①　75.6％
Ａは10ｘ＋ｙ。
これの逆なので、Ｂは10ｙ＋ｘ。

②　58.6％
連立方程式。
『ＢはＡより36小さい』→Ａ－Ｂ＝36

ｘ＝２ｙ　…①
Ａ－Ｂ＝（10ｘ＋ｙ）－（10ｙ＋ｘ）
＝９ｘ－９ｙ＝36　…②
②の項をすべて÷９して、ｘ－ｙ＝４…③

①を③に放り込む。
２ｙ－ｙ＝４
ｙ＝４
①より、ｘ＝２×４＝８
したがって、Ａの値は84。

大問２（平面図形）－32.4％

（１）　65.5％
点Ｃを作るにはＡＥの長さをとりたい。
Ｅは正方形ＡＢＥＦの頂点。∠ＡＢＥ＝90°とＡＢ＝ＢＥを用いる。

①Ｂを通る、直線ＡＢに垂直な線分。
②Ｂを起点にＢＡ＝ＢＥで点Ｅを特定。
③ＡＥの長さをとって、ＢＣに長さを移す。

（２）①　55.8％
Ａ判の話なので、図１・２だけ見る。
Ａ０判の縦がａ。縦：横＝１：√２なので、横は√２ａ。
Ａ１判の短い辺はこの半分で、√２/２ａｃｍ

②　43.8％

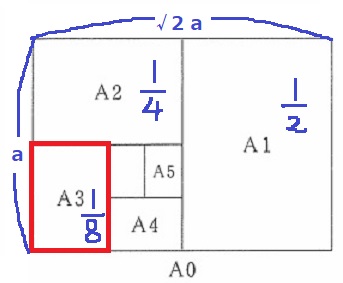
Ａ０判の面積を１とすると、Ａ１判の面積は１/２、Ａ２判は１/４…
Ａ３判は１/８となる。
ａ×√２ａ×１/８＝√２/８ａ²ｃｍ²

（３）①　9.6％!!
Ａ３判とＢ３判における、短い辺の長さの比。
問題文の最後に、『Ａ判とＢ判の数字が同じであれば、
Ａ判の対角線がＢ判の長い方の辺の長さと等しい』とある。

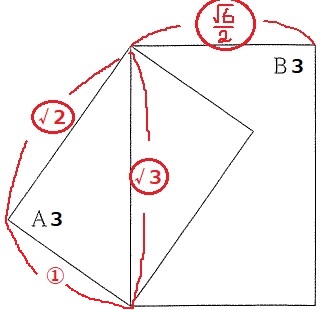
↑図３の０判を３判に変えるとこうなる。
Ａ３の短い辺を①とすると、長い辺は１：√２から〇√２。
三平方の定理から、Ａ３の対角線は〇√３。
これがＢ３の縦となり、横：縦＝１：√２より、
Ｂ３の横は、〇√３×１/√２＝〇√６/２

Ａ３の短い辺…①
Ｂ３の短い辺…〇√６/２
√６/２倍。これを√６＝2.449として小数に直す。
√６/２＝2.449÷２＝1.2245≒1.22倍

②　2.8％!!
今度はＡ３とＢ６の関係性を問う。
先ほど、Ａ３の短い辺を①としたのでＢ６の短い辺を知りたい。

ポイントはＡ判もＢ判も辺の比が１：√２で、
番号が変わっても辺の比は１：√２が維持されるから、すべて相似形であるということ。
（たとえば、Ａ５判とＢ８判はともに辺の比が１：√２で相似）

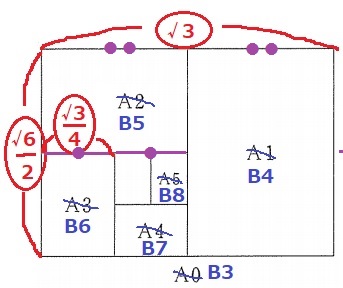
図２のＡ０をＢ３に修正。
すると、Ｂ６は左下の長方形にあたる。
紙は長い辺を半分の長さで切っていく。
Ｂ６の横は、〇√３÷４＝〇√３/４

Ａ３の短い辺…①
Ｂ６の短い辺…〇√３/４
√３/４倍。これを√３＝1.732として小数に直す。
√３/４＝1.732÷４＝0.443＝43.3％≒43％

大問３（関数）－44.7％

（１）　80.8％
Ｃ（－２、８）→Ａ（１、２）
右に３、下に６なので、傾きは－６/３＝－２
Ａから左に１戻ると上に２→切片は４
ｙ＝－２ｘ＋４

（２）　61.6％
変化の割合＝（ｙの増加量）/（ｘの増加量）
ア：（８－２）/（２－１）＝６
もしくは、ｙ＝ａｘ²のｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）で求められる。
ア：２×（１＋２）＝６
イ：２×（－２＋０）＝－４
ウ：２×（０＋２）＝４
エ：２×（－２＋２）＝０
よって、最も大きいのはア。変化の割合は６。

＠別解＠

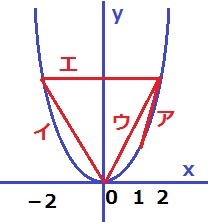
グラフの傾きが最も急であるアが、最も変化の割合が大きい。

（３）　38.6％

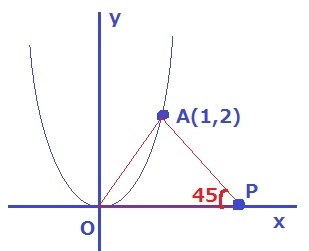
描いてみる。
∠ＡＰＯ＝45°ということは…

Ａからｘ軸に向けて垂線、その足をＱとする。
△ＡＰＱの内角は45°－45°－90°で直角二等辺三角形。
ＡＱ＝ＱＰ＝２
高さ３ｃｍで一括計算する。
よって、回転体の体積は、２×２×π×３÷３＝４π

（４）　15.5％！
四角形ＡＰＱＣが平行四辺形となる。

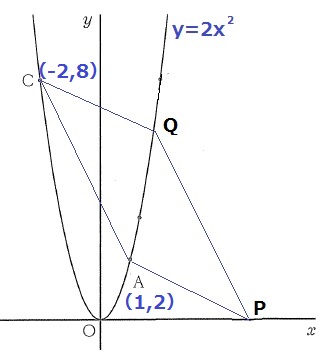
ＡとＣは座標が確定している。
Ｑがグラフ上の点で、ＰはＱより右側のｘ軸上にある。

Ｑはグラフ上にいるので式を立てやすい。
Ｑのｘ座標をｔとおいて、平行四辺形の性質からＱの座標を知りたい。

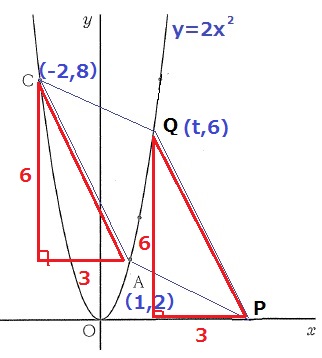
平行線から２つの合同な直角三角形を描くとわかりやすい。
Ａ→Ｃは左に３、上に６移動。
Ｐ→Ｑも左に３、上に６移動。
ここからＱのｙ座標が６とわかる。
Ｑ（ｔ、６）をｙ＝２ｘ²に代入。
６＝２ｔ²
ｔ²＝３
ｔ＞０より、ｔ＝√３
Ｑ（√３、６）
Ｐのｘ座標はＱのｘ座標より３大きいので、Ｐのｘ座標は３＋√３。

大問４（平面図形）－29.7％

（１）　41.0％
△ＡＦＥ∽△ＢＣＥの証明。

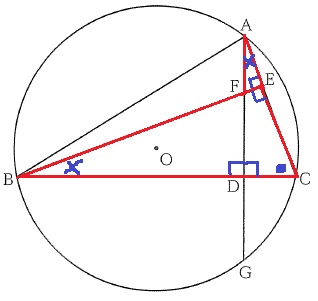
辺の情報がないので、２角にしぼる。
仮定より、∠ＡＥＦ＝∠ＢＥＣ＝90°
∠ＦＡＥ＝×、∠ＡＣＤ＝●とおく。
△ＡＤＣにおいて、●＋×＝180－90＝90°
△ＢＣＥにおいて、∠ＣＢＥ＝180－90－●＝90－●＝×
２角相等→∽

＠別解＠

四角形ＦＤＣＥに注目すると、∠ＦＤＣ＋∠ＣＥＦ＝180°から、
対角の和が180°なので円に内接することになる。
内接する四角形の内角は、その対角の外角に等しいので∠ＡＦＥ＝∠ＢＣＥが導ける。

（２）　31.6％！

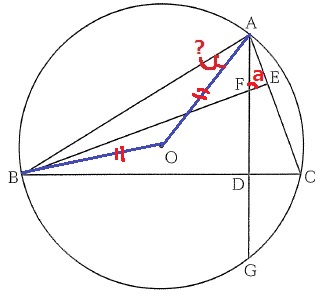
半径より△ＡＢＯは二等辺。
弧ＡＢの中心角である∠ＡＯＢさえわかればよいので、
この円周角にあたる∠ＡＣＢに狙いを定める。

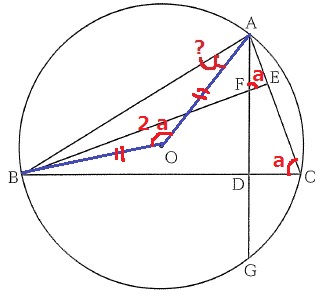
前問の∽から対応する角が等しいので、∠ＡＣＢ＝∠ＡＦＥ＝ａ
中心角は円周角の２倍→∠ＡＯＢ＝２ａ
したがって、∠ＯＡＢ＝（180－２ａ）÷２＝90－ａ°

（３）①　47.8％
ＤＧがわかればＡＧがわかる。
そこで、ＤＧを１辺とする三角形を探す。

ＢＧに補助線。△ＢＤＦと△ＢＤＧに注目する。
（１）の相似＋弧ＣＧに対する円周角で∠ＦＢＤ＝∠ＧＢＤ
共通辺ＢＤと直角を合わせ、一辺と両端角が等しく、△ＢＤＦ≡△ＢＤＧ
ＧＤ＝ＦＤ＝３ｃｍ
よって、ＡＧ＝２＋３＋３＝８ｃｍ

＠別解＠

●ルートでもいける。
対頂角で∠ＢＦＤ＝●
相似で∠ＡＣＢ＝●、弧ＡＢに対する円周角で∠ＢＧＤ＝●
残りの角である∠ＦＢＤ＝∠ＧＢＤが導ける。

②　1.5％!!
円の面積なので半径が欲しい。
本問の図をどうやって中心Ｏと関連付けるかがキーとなる。

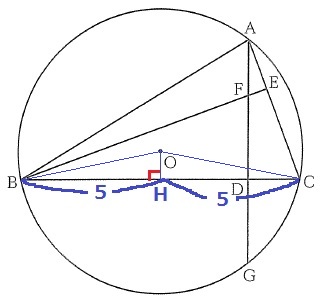
Ｏから弦ＢＣに垂線をひき、足をＨとする。
△ＯＢＨと△ＯＣＨが斜辺（半径）と他の１辺ＯＨが共通する直角三角形で合同。
→ＢＨ＝ＨＣ
ＢＨ＝10÷２＝５ｃｍ
【中心Ｏから弦に向けて垂線をひくと、弦の中点を通る】

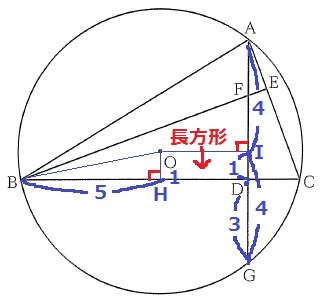
弦ＡＧでも同じことをする。
Ｏから弦ＡＧに向けて垂線、足をＩとおく。
ＩＧ＝８÷２＝４ｃｍ
ＩＤ＝４－３＝１ｃｍ

四角形ＩＨＤＩは４つの角がすべて直角の長方形。
ＯＨ＝１ｃｍ
△ＯＢＨで三平方→半径ＯＢ＝√26ｃｍ
よって、円の面積は、√26×√26×π＝26πｃｍ²