平均22.2点(50点満点、前年比;-0.5点)
問題はこちら→リセマムさん
大問1(計算)
(1)
600×1.1
=600×11/10
=660
(2)
6+(-3)2
=6+9
=15
(3)
(9x+5y)/8-(x-y)/2
={(9x+5y)-4(x-y)}/8
=(5x+9y)/8
(4)
(8a3b2+4a2b2)÷(2ab)2
=(8a3b2+4a2b2)÷4a2b2
=2a+1
(5)
(3x+7)(3x-7)-9x(x-1)
=9x2-49-9x2+9x
=9x-49
(6)
(√5+1)2-√45
=5+2√5+1-3√5
=6-√5
大問2(小問集合)
(1)
x-4=5x+16
4x=-20
x=-5
(2)
x2-3x-1=0
因数分解ができないので解の公式を適用。
x=(3±√13)/2
(3)
yがxの関数である。
➡xの値を決めると、それに伴ってyの値がただ1つに決まる関係。
中1で習うが、学テの正答率は悪かった。
ア:y=x2で関数。〇
イ:多角形の外角の和は常に360°。
頂点の数と外角の数は等しく正多角形だから、y=360/xで関数。〇
ウ:降水確率から最高気温は算出できない。×
エ:y=0.03xで関数。〇
オ:何倍したかがわからないと倍数はわからない。×
ア・イ・エ
(4)
整数の証明問題。
説明通りに記述すれば良いが、中央の数をnとおいている点に注意。
残りの2つの数は、n-6、n+6と表される。
3つの数の和は、(n-6)+n+(n+6)=3n
3nは中央の値だから、3nは中央の数の3倍である。
(5)
難しい。
△BPCの面積が△ABCと等しい。
BCが共通なので、Aが動くことになる。

AをBCについて反対側に対称移動させる。
AからBCに向けて垂線をひき、BAを長さをとって下側へ移動。
交点がA’となる。
△ABCと△A’BCは底辺と高さが同じで面積が等しい。

A’を通る垂線を作図。90°の同位角で、BCに平行な直線である。
等積変形の要領で△A’BCと△PBCが等しくなる。
A’を通る垂線と円との交点がPとなる。
①Aを通るBCの垂線。
②BAをとり、AをBCについて対称移動→A’
③A’を通る垂線。円との交点がP。
(6)①
条件が特殊。
奇数はそのままだが、偶数は÷2をする。
サボはy=xとなる座標ごとで整理しました。
(1、1)(1、2)(2、1)(2、2)
(4、4)
(3、3)(3、6)(6、3)(6、6)
(5、5)
以上、10通り
確率は、10/36=5/18
*(2、4)(4、2)は×。
②
頭がこんがらがってくる。。

Oから距離4で円を作成。その内部にある格子点を調べる。
(1、1)と(2、2)は前問で5通りと出している。
(2、1)→(4、1)(4、2)
(3、1)→(3、1)(3、2)(6、1)(6、2)
(3、2)→(3、4)(3、6)
*偶数は必ず2倍するが、奇数は2倍するか否かで2通りある。
右下の3点が8通りで、対称性から左上の3点も同じ8通り。
合計5+8×2=21通り
確率は、21/36=7/12
@別解@
余事象でもいけなくもない。
偶数が出てしまうと、最大の6でも3に減るので4以下になる。
ということは、少なくとも5を出せば円外にある。
5と(1~6)を出すパターンは、6×2-1=11通り
*ひっくり返しで×2、(5、5)は重複するので-1をしている。
注意点は、(3、3)も円外にあること!
(3、3)(3、6)(6、3)(6、6)の4通りも除外。
合計15通りだから、4以下は36-15=21通りとなる。
(7)①
グラフの時間が分なので、おのおのの分速を求める。
大輔は時速18kmだから、18000m÷60分=分速300m
バスは9kmを15分で進むので、9000m÷15分=分速600m
速さの比は、大輔:バス=300:600=①:②

中学受験の戦法を使わせていただきます。
2回目のすれ違いから垂線をひく。
この長さは駅からの距離。同じ距離を走るのにかかる時間の比は速さの逆比。
大輔:バス=②:①
したがって、10+(35-10)×②/③=26・2/3分=26分40秒
午前10時26分40秒
②

追い越しに目をつけよう。
2回目の追い越しが起こるのは、大輔が45分より遅くに着いたときだが、
このとき、すれ違う回数は3回しかない・・。
すれ違いが1回増えるのは50分を超えたとき。
(*グラフの交点は追い越しとすれ違いが同時に起こるだけなので、回数に影響はない)
9kmを40分で走るので、9km×60/40=時速13.5km
大輔のグラフを右に移動させると、60分を超えたら3回目の追い越しが起きてしまう。
つまり、60分(午前11時)までが範囲。
9kmを50分で走るので、9km×60/50=時速10.8km
10.8≦a<13.5
*不等号に注意!
大問3(データの活用)
(1)
177cmは175~180cmの階級に含まれる。
階級値は175と180の平均である177.5cm。
(2)
最頻値(モード)は最もあらわれている値。
26.5cm
(3)
仮の平均を27cmとする。
(-2.5)×2+(-2)×6+(-1.5)×8+(-1)×14+(-0.5)×18+0×17+0.5×16+1×11+1.5×6+2×2…

↑こんな感じで相殺していくと、
(-2.5)×2+(-2)×4+(-1.5)×2+(-1)×3+(-0.5)×2+0×27
=-5-8-3-3-1=-20
平均値は、27+(-20)÷100=26.8cm
100人の中央値(メジアン)は50番目と51番目の平均で27cm。
中央値の方が0.2cm大きい。
ア…中央値、イ…0.2
(4)
熊本県:県外=2:98=1:49
熊本出身が36人だから県外は、
36×49=36×(50-1)=1800-36=1764人
大問4(空間図形)
(1)
AB=6cm、AM=2cm
△ABMで三平方→AM=4√2cm
(2)
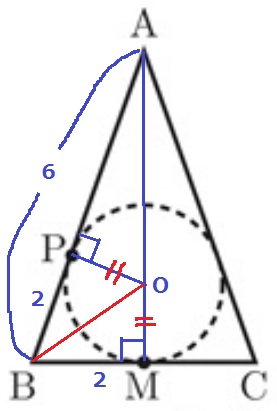
内接円の中心をOとする。
OBに補助線。半径OPと接線ABは垂直。
∠OMB=∠OPB=90°、半径OM=OP、共通辺OB
→斜辺と他の1辺が等しい直角三角形で△OBM≡△OBP
BM=BP=2cm
AP=6-2=4cm
(3)①
小問でもよくでてくる。
中心角は〔×半径/母線〕で処理。
6×6×π×2/6=12πcm2
②
展開図の作成。
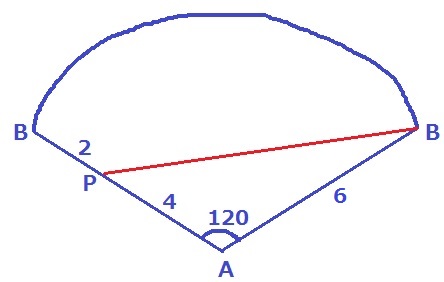
PBを求めたいので、PBを斜辺とする直角三角形をつくりたい。
前問で半径/母線が1/3だったので、中心角は360×1/3=120°
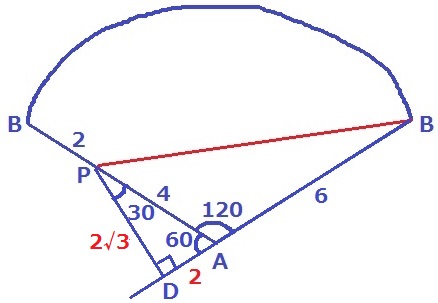
Pから垂線をひき、BAの延長線との交点をDとする。
△APDの内角は30°-60°-90°の直角三角形で、辺の比は1:2:√3
PD=2√3cm、DA=2cm
△PBDで三平方→PB=2√19cm
大問5(関数)
(1)
y=1/8x2にxの値を代入する。
A(-4、2)B(6、9/2)
A→Bは右に10、上に9/2-2=5/2移動する。
傾きa(変化の割合)=yの増加量÷xの増加量=5/2÷10=1/4
傾きが1/4ということは、右に4いくと上に1移動する。
A座標が-4なので、Aから右に4、上に1移動して切片は2+1=3
y=1/4x+3
(2)
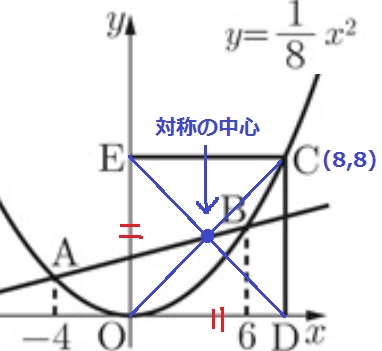
C座標はx座標とy座標が等しい→y=x
x=1/8x2
x2-8x=x(x-8)=0
Cのx座標は正→x>0より、x=8
C(8、8)
対称の中心は正方形の真ん中、すなわち、対角線の交点にあたる。
Cのx座標とy座標を÷2して(4、4)
ア(8、8)、イ(4、4)
*(4、4)はAB上の点だから、ABは正方形ODCEを2等分する。
(3)
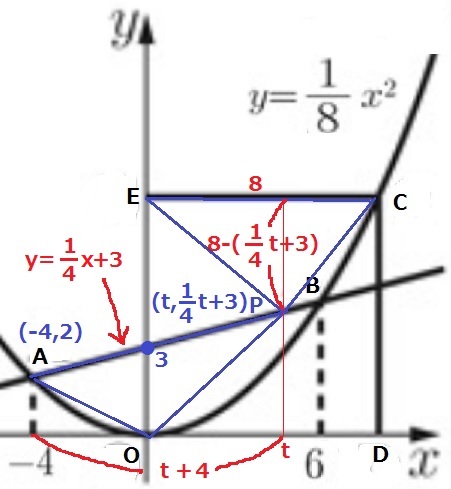
Pのx座標をtとおく。P(t、1/4t+3)
△OPAの面積…(t+4)×3÷2
△PCEの面積…8×{8-(1/4t+3)}÷2
(t+4)×3=8×(5-1/4t)
3t+12=40-2t
5t=28
t=28/5
これをy=1/4x+3のxに代入。
y=1/4×28/5+3=22/5
P(28/5、22/5)
大問6(平面図形)
(1)
△CDF∽△EACの証明。
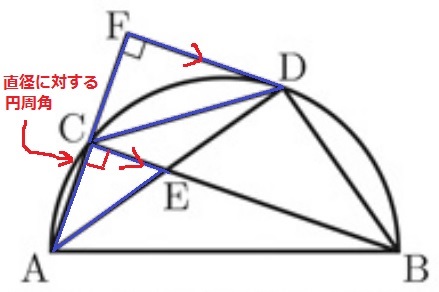
半円の弧に対する円周角から、∠ACE=90°
問題はもう1つの等角。
∠ACE=∠CFDで同位角が等しいので、CE//FD
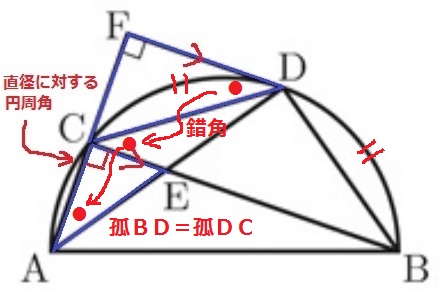
錯角→弧BDの円周角=弧DCの円周角が等しい。
2角が等しく∽
(2)
相似図形が5つもある。
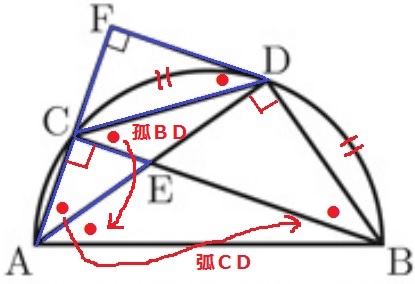
わかりやすい目印は3つの直角。
孤BDと弧CDに対する円周角から、∠DAB=∠CBD=●
直角と●で2角相等となる三角形を探す。
△DAF・△EBD・△BAD
(3)
ラストに説明問題が登場したが、とてもやりづらい。
具体的な数値が与えられたので、相似から長さを計算してCがAFの中点であることを説明する。
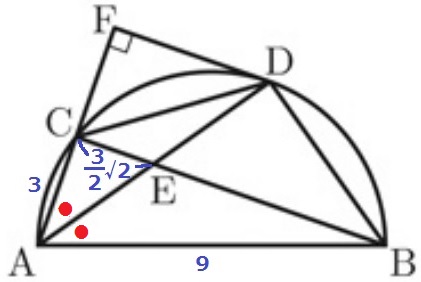
初手は角の二等分線の定理かと思われる。
発展事項に分類されるが、原理は中学レベルの相似なので定理は知っておいて損はない。
AC:AB=CE:EB
CE=6√2×3/12=3√2/2
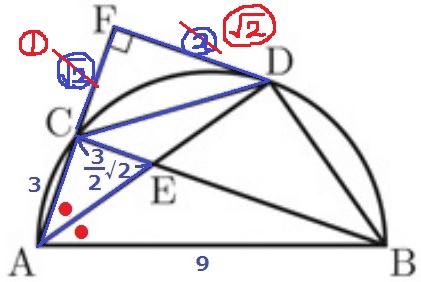
ここで’(1)の相似を用いる。
EC:CA=CF:FD
=3√2/2:3=√2:2
CFの長さが知りたいので、CFの比は①としておくと計算がしやすい。
CF:FD=√2:2=1:√2
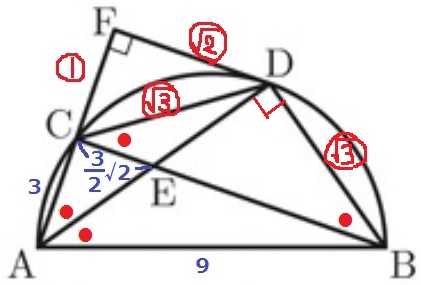
△CDFで三平方→DC=〇√3
弧BD=弧DC→∠DBC=∠DCB→△DBCは二等辺なので、DB=〇√3
①をxに置き換えて、△ADFと△ABDで三平方。
AF2+FD2=AD2=AB2-DB2
(3+x)2+(√2x)2=92-(√3x)2
9+6x+x2+2x2=81-3x2
6x2+6x-72=0
x2+x-12
=(x+4)(x-3)=0
x>0より、x=3
AC=CF=3cmより、CはAFの中点である。
@別解@
YAさんから素晴らしい解法を頂きました。
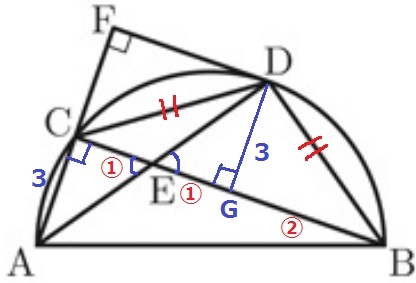
角の二等分線の定理でCE:EB=①:③
DからCBに垂線をひき、交点をGとします。
孤DB=孤DC→弦DB=弦DC→△DBCは二等辺三角形で、
頂角を通る垂線は底辺を二等分しますからCG=②
CE=EG=①
直角と対頂角を合わせると、1辺と両端角相等で△CAE≡△GDE
DG=AC=3cm
四角形FCGDは4つの角が直角である長方形。
対辺が等しく、FC=AC=3cm
*6√2の誘導を完全無視したのは、作問者の想定外かもしれない。
●講評●
平均が4割4分で難しかった。
大問1
得点を稼いでおきたい。
大問2
(5)以降が苦しい。
(5)Aを下へ持ってくる点に気付けるか。
(6)特殊な条件で、漏れなく調べあげるのは大変であった。
(7)ここで時間を使いすぎると後半が間に合わない。
すれちがい4回、追い越し2回と条件のハードルが高くなっている。
大問3
(3)平均は仮の計算を使わないとしんどい。仮の平均を使ってもしんどい…。
大問4
めずらしい形式ではない。(3)②中心角を調べること!
大問5
(3)求めたいPの座標を文字におきかえる。
ここも典型パターンだが、処理ミスを防げたか否か。
大問6
(3)難しかった。どれだけ時間を残せたかにもよる。
CFを直接求めにいくほか、EがADの中点である点を指摘する方法もある。



コメント