2022年度　静岡県公立高校入試問題過去問【数学】解説

平均24.64点（前年比；＋2.25点）

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）ア　97.2％
６＋８×（－３）
＝６－24
＝－18

イ　92.8％
（８ａ²ｂ＋36ａｂ²）÷４ａｂ　←分配法則
＝８ａ²ｂ÷４ａｂ＋36ａｂ²÷４ａｂ
＝２ａ＋９ｂ

ウ　93.3％
（４ｘ＋ｙ）/５－（ｘ－ｙ）/２
＝｛２（４ｘ＋ｙ）－５（ｘ－ｙ）｝/10
＝（８ｘ＋２ｙ－５ｘ＋５ｙ）/10
＝（３ｘ＋７ｙ）/10

エ　73.3％
√７（９－√21）－√27　←√21＝√７×√３
＝９√７－√７（√７×√３）－３√３
＝９√７－７√３－３√３
＝９√７－10√３

（２）　88.2％
（ａ－５）（ａ－６）－ａ（ａ＋３）
＝ａ²－11ａ＋30－ａ²－３ａ
＝－14ａ＋30　←ここで代入
＝－14×２/７＋30
＝－４＋30＝26

（３）　86.5％
（ｘ－２）²＝16
ｘ－２＝±４
ｘ＝２±４
ｘ＝－２、６

大問２（小問集合）

（１）　80.8％

①『２点Ａ、Ｂから等距離にある』→ＡＢの垂直二等分線
②Ａを通る垂線
これらの交点がＰ。

（２）　50.0％
４Ｌ＝4000ｍＬに変換しておく。
ｘが『水がなくなるまでの時間』で、ｙは『１時間当たりの水の減る量』
１時間あたりｙｍＬずつ減り、ｘ時間後に4000ｍＬ減る。
→ｘｙ＝4000（反比例）
ｙ＝4000/ｘ
*誤答では、ｙ＝４/ｘが目立つ。

（３）　50.1％
６個から２個取り出す→₆Ｃ₂＝15通り
正の数に０は含まれない点に注意！
－３と－２が出たら×。
（－１、２）（０、１）（０、２）（１、２）の４通り。
確率は４/15。
*誤答では２/５が目立つ。

大問３（データの活用）

（１）　58.6％
範囲（レンジ）＝最大値－最小値
12－１＝11
*誤答では12が目立つ。

（２）　10.5％！
10個の中央値（メジアン）は５番目と６番目の平均。
2010-19年の中央値は４日と６日の平均→５日。
これが2011-20年は６日と７日の平均→6.5日になった。
ということは、2010年は４日以下で、2020年は７日以上である。

平均値は＋0.3日。データは10個だから総和は0.3×10＝３日増えた。
１～４日のうち＋３して７日以上となるのは、４＋３＝７しかない。
したがって、2010年は４日、2020年は７日。

大問４（方程式）

38.5％
答案では計算の過程も記述する。
Ａのメダカをｘ匹、Ｂのメダカをｙ匹とする。
メダカは全部で86匹だから、
ｘ＋ｙ＝86　…①

もう１つはＣのメダカの数で等式を立てる。
Ａから１/５ｘ匹、Ｂから１/３ｙ匹をＣに移動する。
これがＡの残り４/５ｘ匹より４匹少ない。
１/５ｘ＋１/３ｙ＝４/５ｘ－４
整理すると、９ｘ－５ｙ＝60　…②
これを解くと、ｘ＝35、ｙ＝51
Ｃに移したメダカは、35×１/５＋51×１/３＝24匹
*どのような数量をｘやｙで表しているのかを明記していないものが目立つ。

＠余談＠
本問は方程式強制ですが、
こういうのを意地でも算数で解きたくなる性分(;^ω^)

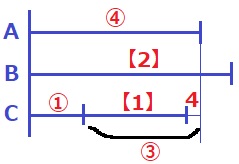
最初のＡを⑤、Ｂを【３】として、
Ｃに①、【１】を譲渡したあとの様子。
③＝【１】＋４に注目する。
【１】＝③－４
【３】＝⑨－12
Ｃに譲渡する前のＡとＢの合計が86匹だから、
⑤＋【３】
＝⑤＋（⑨－12）
＝⑭－12＝86
①＝７匹
【１】＝③－４＝21－４＝17匹
よって、７＋17＝24匹

大問５（空間図形）

（１）　60.7％
△ＡＤＰの底辺をＡＤとすると、高さＰＤは６×２÷３＝４ｃｍ
ＰはＥＤ上にあるので、ＰＥ＝12－４＝８ｃｍ
Ｐは毎秒１ｃｍだから８秒後。
*誤答では４が多い。

（２）　35.0％
Ｐは14ｃｍ移動する→ＰはＡＤ上のＤから２ｃｍ先。

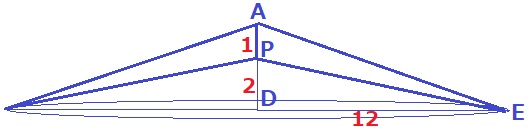
回転体の底面は半径12ｃｍの円で、高さ３ｃｍの円錐から高さ２ｃｍの円錐をひく。
⇒高さは１ｃｍで計算する。
12×12×π×１÷３＝48πｃｍ³
*誤答では48や144πがみられる。

（３）　5.7％!!
最短距離なので展開図を作成。

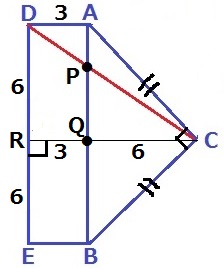
ＣからＤＥに垂線をひき、ＡＢ・ＤＥとの交点をＱ・Ｒとする。
△ＡＢＣは直角二等辺三角形で、ＱとＲはＡＢとＤＥの中点にある。
ＤＲ＝12÷２＝６ｃｍ
また、△ＡＣＱも直角二等辺でＣＱ＝ＡＱ＝６ｃｍ
△ＤＣＲ∽△ＰＣＱより、ＰＱ＝６×６/９＝４ｃｍ

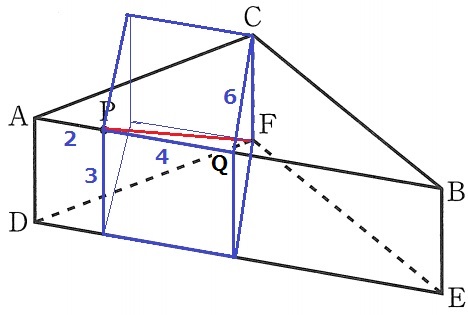
ＰＦを対角線とする直方体をつくる。
１辺がａ、ｂ、ｃの直方体の対角線の長さ→√（ａ²＋ｂ²＋ｃ²）
ＰＦ＝√（４²＋６²＋３²）
＝√61ｃｍ
*無答も多い。

大問６（関数）

（１）　73.5％
ｙ＝ａｘ²（ａ＞０）は下に凸のグラフ。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－３のとき、最大値ｙ＝９ａ
０≦ｙ≦９ａ

（２）　61.8％
平行なので傾きは－３。
Ｃ（－２、－３）から右に２、下に６移動して、切片は－３－６＝－９
ｙ＝－３ｘ－９
*誤答では、ｙ＝－３ｘ＋３がみられる。

（３）　18.1％！
答案では求める過程も記述する。

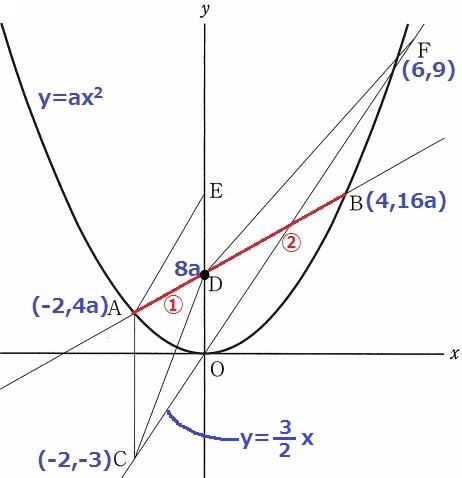
ｙ＝ａｘ²のａを求めたい。
このグラフ上にある点の座標をａで表してみる。
Ａ（－２、４ａ）Ｂ（４、16ａ）
三角形と四角形の面積を求めるうえで、頂点の切片Ｄがポイントになる。
ｘ座標の差より、ＡＤ：ＤＢ＝２：４＝①：②
切片Ｄのｙ座標は、４ａ＋12ａ×①/③＝８ａ
（*内分点の公式を知っている人は、（４ａ×２＋16ａ×１）/（１＋２）＝24ａ/３＝８ａ）
また、ＣＯ；ｙ＝３/２ｘにｙ＝９を代入して、Ｆ（６、９）

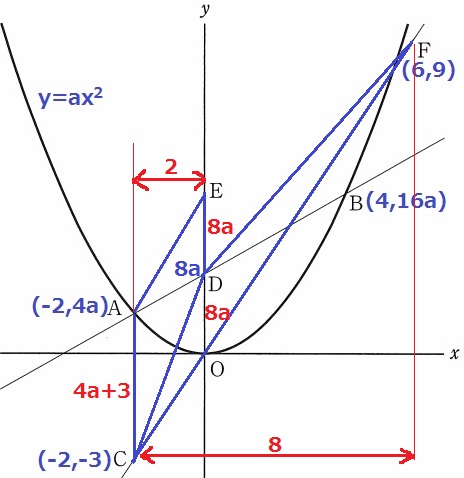
ＥＤ＝ＤＯ＝８ａ
△ＤＣＦ＝８ａ×８÷２＝32ａ
四角形ＡＣＤＥ＝（８ａ＋４ａ＋３）×２÷２＝12ａ＋３

△ＤＣＦ＝四角形ＡＣＤＥ×２
32ａ＝２（12ａ＋３）
ａ＝３/４
*問題を解くのに必要な点の座標を正しく求められないための誤答が目立つ。
無答も多い。

＠別解＠

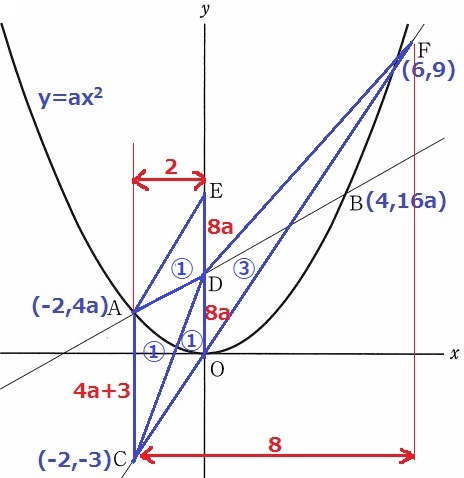
必要な数値がそろったら、面積比の方が処理しやすいかもしれない。
△ＤＣＯ＝①とする。
ｘ座標の差の比から△ＤＯＦ＝③
△ＤＣＦ＝④で、四角形ＡＣＤＥ＝②になる。

ＥＤ＝ＤＯより、△ＥＡＤ＝△ＤＣＯ＝①
△ＡＣＤ＝②－①＝①
△ＡＣＤ＝△ＤＣＯとなり、図はいい加減だが一応ＡＣ＝ＤＯになる。
４ａ＋３＝８ａ
ａ＝３/４

大問７（平面図形）

（１）　23.7％！
△ＡＧＤ∽△ＥＣＢの証明。

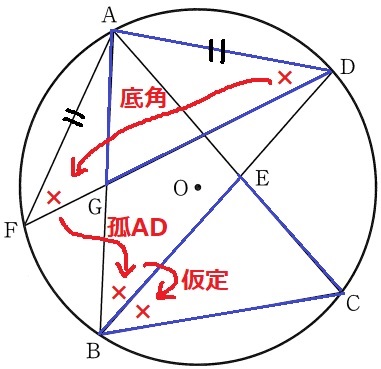
二等辺三角形ＡＤＦの底角→弧ＡＤに対する円周角→仮定とつなげて、
∠ＡＤＧ＝∠ＥＢＣ

もう１つの等角が難しい(;´Д｀)
いったん何かをはさんだ方が良い。

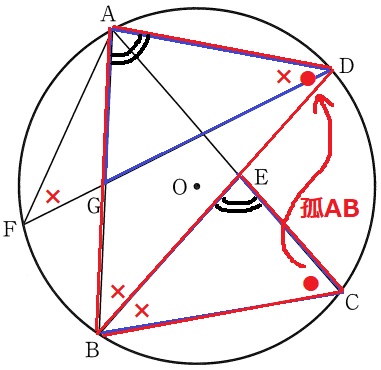
孤ＡＢに対する円周角で∠ＢＣＥ＝∠ＢＤＡ
×と●の２角相等で△ＥＣＢ∽△ＡＤＢ
対応する角は等しいから、∠ＢＥＣ＝∠ＢＡＤ
∠ＢＡＤ＝∠ＧＡＤなので、∠ＧＡＤ＝∠ＣＥＢ
２角相等で△ＡＧＤ∽△ＥＣＢ
*「２組の角がそれぞれ等しい」において、∠ＡＤＧ＝∠ＥＢＣは説明されているが、
もう１組の対応する角が等しい理由について、論理の飛躍をしているものや説明不十分が目立つ。

（２）　12.1％！

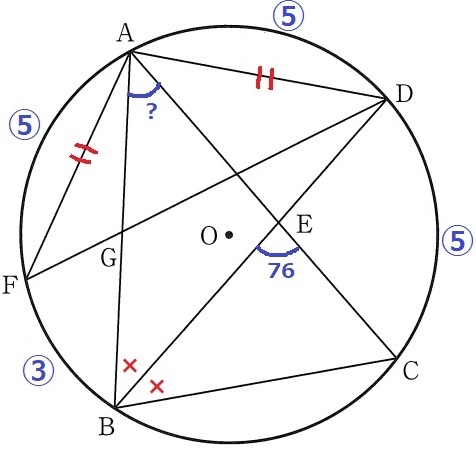
最初は孤に注目する。
孤ＡＦ＝⑤、孤ＦＢ＝③とする。
ＡＦ＝ＡＤより、孤ＡＤ＝⑤
∠ＡＢＤ＝∠ＤＢＣで円周角が等しいから、孤ＤＣ＝⑤

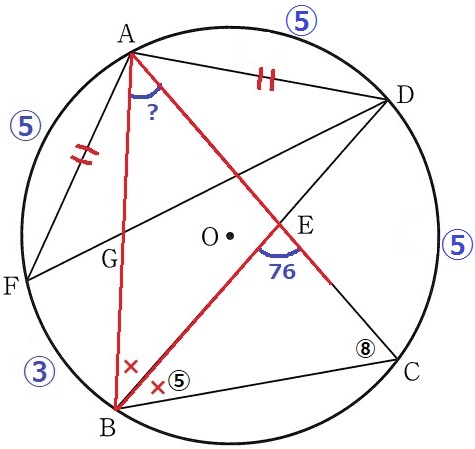
次に△ＢＣＥの内角に注目する。
∠ＥＢＣ：∠ＥＣＢ＝孤ＤＣ：孤ＡＢ＝⑤：⑧
∠ＥＢＣ＝（180－76）×⑤/⑬＝40°
∠ＡＢＥ＝40°
最後に△ＡＢＥで外角定理を適用。
∠ＢＡＣ＝76－40＝36°
*誤答では38などがみられる。無答も多い。