2022年度　徳島県公立高校入試問題過去問【数学】解説

平均42.9点（前年比；－4.0点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
－７－（－３）
＝－７＋３
＝－４

（２）
18×（５ｘ－２ｙ）/６　←18と６を約分
＝３（５ｘ－２ｙ）
＝15ｘ－６ｙ

（３）
√25＜√30＜√36
√30未満で最大の整数は５。

（４）
３ｘ²－36＝０
３ｘ²＝36
ｘ²＝12
ｘ＝±２√３

（５）
ゼリーは６ａｇ、箱はｂｇで和が800ｇ未満であった。
６ａ＋ｂ＜800

（６）
反比例はｘとｙの積が比例定数ａで一定。
ａ＝４×５/４＝５
ｙ＝５/ｘ

（７）
昇順にすると、【５、７、７、８、10、11、13、14、16、19、20】
Ｑ2（第２四分位数；中央値）は、（11＋１）÷２＝６番目の値で11。（箱ひげ図に記載済み）
Ｑ1（第１四分位数）は下位５つの真ん中で、下から３番目の５点。
Ｑ3（第３四分位数）は上位５つの真ん中で、上から３番目の16点。
ａ…７、ｂ…16

（８）

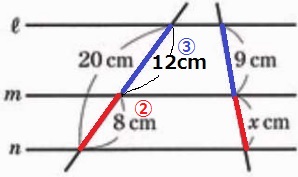
平行線と線分の比。
12：８＝３：２＝９：ｘ
ｘ＝２×９/３＝６

（９）
出目の和は最大で12。
12までの素数を調べていく。
●２→（１、１）
●３→（１、２）と逆。
●５→（１、４）（２、３）と逆。
●７→（１、６）（２、５）（３、４）と逆。
●11→（５、６）と逆。
合計15通り。
全体は６×６＝36通りだから、確率は15/36＝５/12

（10）
定規とコンパスを持っていない場合は文章で代用できるらしい(ﾟДﾟ)

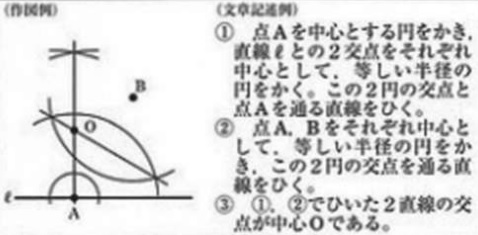
①円はＡを接点とし、半径と接線ℓは直交する。
　Ａを通る垂線上に中心Ｏがある。
②円周上にＢがくる。中心ＯはＡＢの垂直二等分線上にある。
これらの交点がＯ。

大問２（方程式）

（１）
５枚から３枚を選ぶ→５枚から選ばない２枚を選ぶ。
₅Ｃ₂＝10通り

（２）ａ

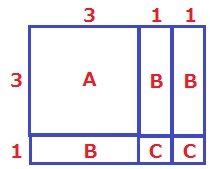
並べちゃった方が早いと思う(;^ω^)
もし、計算で出すならば、全体の長方形の面積から求める。
３×３×１＋３×１×３＋１×１×２＝20ｃｍ²
【20→１×20、２×10、４×５】
Ａは１辺３ｃｍの正方形だから、長方形の辺は３ｃｍ以上。４×５しかない。
４ｃｍ、５ｃｍ

ｂ
長方形の面積から考える。
Ａ＋Ｂ＋Ｃ
＝ｘ²＋６ｘ＋８＝（ｘ＋２）（ｘ＋４）
長方形の縦をｘ＋２ｃｍ、横をｘ＋４ｃｍとすると、
周の長さは、｛（ｘ＋２）＋（ｘ＋４）｝×２＝４ｘ＋12ｃｍ

ｃ
ここも面積で方程式を立てる。
みさき…（ｘ＋７）²＝ｘ²＋14ｘ＋49
かずき…ｘ²＋６ｘ＋８
みさきは、かずきより105ｃｍ²大きかったので、
ｘ²＋６ｘ＋８＋105＝ｘ²＋14ｘ＋49
８ｘ＝64
ｘ＝８

大問３（数量変化）

（１）ア
7000＋（800＋400）×５
＝7000＋6000
＝13000円

イ
Ａ社は１枚あたり900＋600＝1500円ずつ増加する→傾きは1500
基本料金3500円は定数→切片は3500
1500ｘ＋3500

ウ
Ａ社…ｙ＝1500ｘ＋3500
Ｂ社…ｙ＝1200ｘ＋7000

交点のｘ座標を求める。
1500ｘ＋3500＝1200ｘ＋7000
300ｘ＝3500
ｘ＝35/３
（*計算上では35/３枚でＡ社とＢ社の料金が同じになる。
Ｔシャツの枚数は整数だから11枚以下はＡ社、12枚以上はＢ社が安くなる）

（２）ａ
基本料金…11000円
Ｔシャツ代…800円（25枚分）、プリント代…400円（20枚分）
20枚までは１枚につき1200円、余分の５枚は１枚につき800円かかる。
11000＋1200×20＋800×５
＝11000＋24000＋4000
＝39000円

ｂ

Ｃ社のグラフを追記する。
０≦ｘ≦20では、いずれも傾きが1200で平行。
Ｃ社のグラフはＢ社より常に上側にあり、Ｂ社の方が安い。

平行四辺形の対辺は等しい。
ｘ＝20のＢ社とＣ社の差（赤線）は切片の差と同じで、11000－7000＝4000円
ｘ＞20からＢ社は＋1200円、Ｃ社は＋800円増加するので、
差は400円ずつ縮まるから、4000÷400＝10枚で差が埋まる。
交点のｘ座標は、20＋10＝30枚
30枚で両社の値段が等しくなるので、31枚以上からＣ社が安くなる。
エ…平行、オ…上、カ…30、キ…31

大問４（関数）

（１）
Ａ（－４、６）を点Ｏを回転の中心として点対称移動させる。
⇒原点Ｏに対して対称な点は（４、－６）

（２）

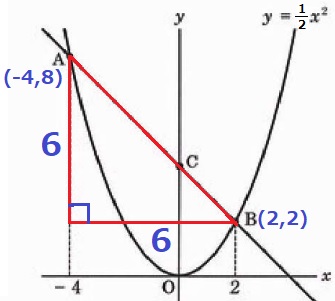
ｙ＝１/２ｘ²におのおののｘ座標を代入する。
Ａ（－４、８）Ｂ（２、２）
ＡＢを斜辺とする直角三角形を作成する。
等辺が６ｃｍの直角二等辺→辺の比は１：１：√２でＡＢ＝６√２

（３）ａ

ｙ＝ｘ²に代入してＡとＢの座標を確定する。
Ａ（－４、16）→Ｂ（２、４）
右に６、下に12だから傾きは－２。
切片はＢから左に２、上に４移動して、４＋４＝８
上図のように等積変形して、△ＯＡＢの面積は６×８÷２＝24

ｂ
難しい(´Д｀)

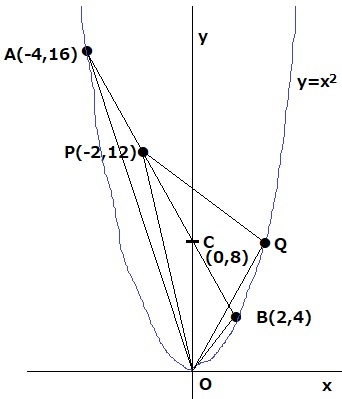
ＰはＡ（－４、16）とＣ（０、８）の中点→Ｐ（－２、12）
△ＯＡＢと△ＯＰＱはどの辺もかぶっていない(;´･ω･)
どこかで等積変形を試みようとしても厳しい。。

前問で△ＯＡＢの面積は24と出ている。いっそのこと△ＯＡＢを無視し、
△ＯＰＱに等積変形しやすい、面積が24の三角形をつくってしまう。

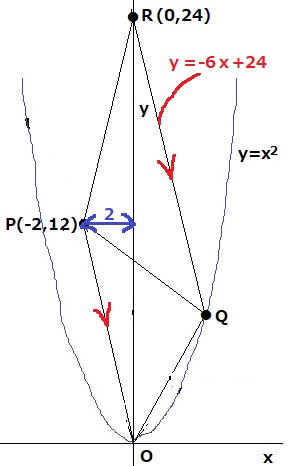
△ＯＰＱのうち、辺ＯＰの位置は決まっている。
そこで、ＯＰを底辺としてＱに移動できるＲをｙ軸上に設定する。
ＲはＱを通るＰＯに平行な線でｙ軸との交点である。

△ＯＰＲの面積が24。
高さはＰのｘ座標から２、底辺ＯＲは24×２÷２＝24
⇒Ｒ（０、24）
ＰＯの傾きは－６。ＲＱの式はｙ＝－６ｘ＋24
Ｑはとｙ＝ｘ²とｙ＝－６ｘ＋24の交点だから、
ｘ²＝－６ｘ＋24
ｘ²＋６ｘ－24＝０
解の公式を適用。ｘの係数が偶数なのでｂ＝２ｂ’が使える。
ｘ＞０より、ｘ＝－３＋√33

＠別解＠
求めたいＱのｘ座標をｔとして方程式を立てることもできる。

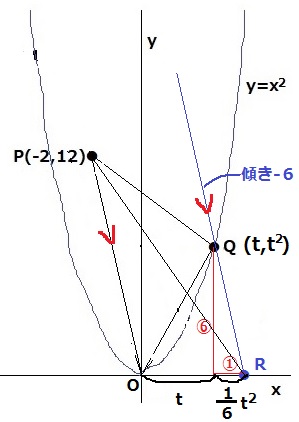
平行線を頼りに、Ｑをｘ軸に移してＲとする。
傾きは－６なので、Ｑから⑥下がって、右に①移動するとＲ。
⑥＝ｔ²だから、①＝ｔ²×①/⑥＝１/６ｔ²
ＯＲ＝１/６ｔ²＋ｔ
△ＯＰＲの面積から、（１/６ｔ²＋ｔ）×12÷２＝24
ｔ²＋６ｔ－24＝０
これを解くと、ｔ＝－３＋√33（ｔ＞０）

大問５（平面図形）

（１）ａ

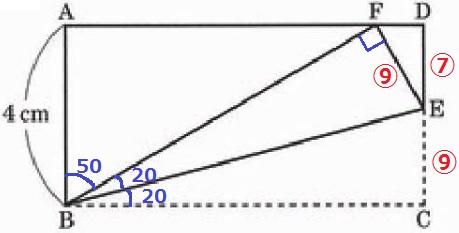
折り返しで∠ＥＢＣ＝∠ＥＢＦ
∠ＥＢＦ＝（90－50）÷２＝20°
△ＥＢＦの内角より、∠ＢＥＦ＝180－（20＋90）＝70°

ｂ
折り返しで、ＥＦ＝ＥＣ＝⑨
４ｃｍ＝⑯なので、ＥＦ＝４×⑨/⑯＝９/４ｃｍ

（２）ａ
△ＡＢＱ≡△ＰＤＱの証明。

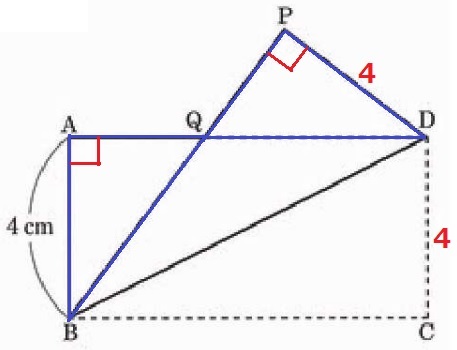
長方形の対辺と折り返しから、ＡＢ＝ＰＤ
長方形の１つの内角で、∠ＱＡＢ＝∠ＱＰＤ

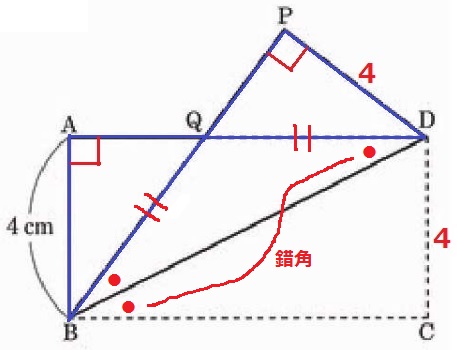
折り返しで、∠ＱＢＤ＝∠ＣＢＤ
ＡＤ//ＢＣの錯角で、∠ＣＢＤ＝∠ＱＤＢ
△ＱＢＤは２つ底角が等しいから二等辺三角形→ＱＢ＝ＱＤ
斜辺と他の１辺が等しく、△ＡＢＱ≡△ＰＤＱ

＠別解＠

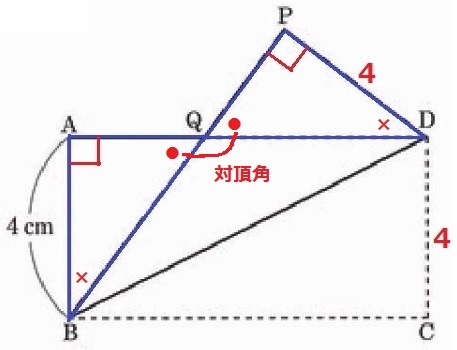
公式解答では、対頂角（●）を指摘して残りの角（×）が等しいので、
１辺と両端角を用いて合同を導いている。

ｂ
むつかしい:;(∩´＿`∩);:

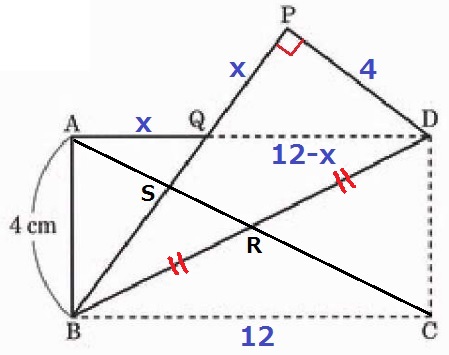
四角形ＲＤＰＳと△ＢＲＳの面積比が知りたい。
Ｒは長方形の対角線の交点で位置がはっきりしているが、Ｓが不明。
長さが４と12しかないので、他にわかるところを探す。

ＡＱ＝ｘとおくと、ＱＤ＝12－ｘ
前問の合同から対応する辺より、ＰＱ＝ｘ、ＰＤ＝４
△ＰＤＱで三平方→ｘ²＋４²＝（12－ｘ）²
24ｘ＝128
ｘ＝16/３

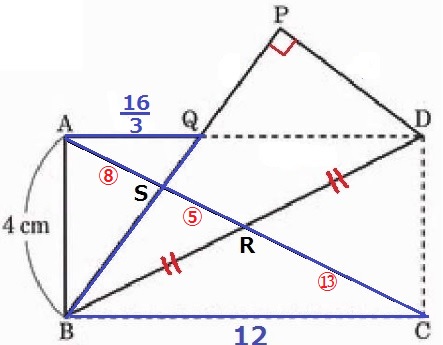
ＡＱを１辺とする相似を探す。
△ＡＱＳ∽△ＣＢＳより、ＲがＡＣの中点であることを踏まえると、
ＡＳ：ＳＣ＝16/３：12＝⑧：⑱→ＡＳ：ＳＲ：ＲＣ＝⑧：⑤：⑬

ここからが迷う(´ﾟдﾟ｀)
ＢＳ：ＳＰがわかれば隣辺比で決着するが、上にあるＰの位置が求めにくい。
ＡＳ：ＳＲから△ＢＳＡ：△ＢＲＳ＝⑧：⑤がわかるので…

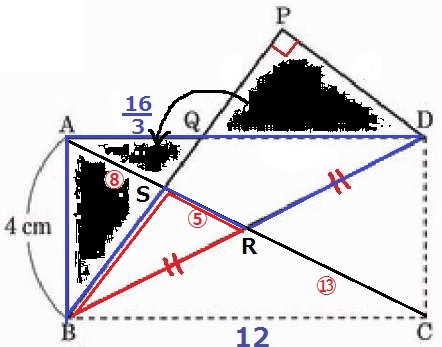
前問の合同を頼りに△ＰＤＱを△ＡＢＱに移植する。
四角形ＲＤＰＳ：△ＢＲＳ→五角形ＡＢＳＲＤ：△ＢＲＳ

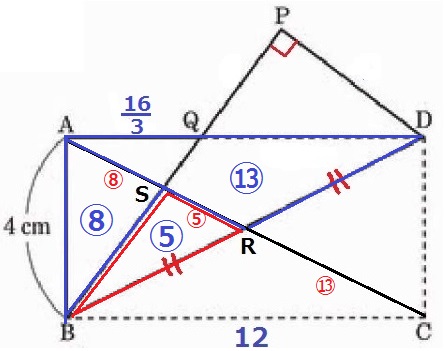
△ＢＳＡ：△ＢＲＳ＝⑧：⑤
長方形の対角線は長方形の面積を４等分するから、
△ＡＲＤ＝△ＡＢＲ＝⑬
五角形ＡＢＳＲＤ：△ＢＲＳ＝四角形ＲＤＰＳ：△ＢＲＳ＝㉑：⑤ 
四角形ＲＤＰＳは△ＢＲＳの21/５倍。