問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
３＋２×（－３）2
＝３＋２×９
＝21
（２）
２（ｘ＋３ｙ）－（ｘ－２ｙ）
＝２ｘ＋６ｙ－ｘ＋２ｙ
＝ｘ＋８ｙ
（３）
（√２＋１）/３－１/√２
＝（√２＋１）/３－√２/２
＝｛２（√２＋１）－３√２｝/６
＝（２－√２）/６
（４）
ｘ2＋５ｘ－６
＝（ｘ＋６）（ｘ－１）
（５）
２ｘ2＋３ｘ－４＝０
解の公式を適用して、ｘ＝（－３±√41）/４
（６）
ｙ＝－２ｘ＋１について、
ｘ＝－１のとき、最大値ｙ＝３
ｘ＝２のとき、最小値ｙ＝－３
－３≦ｙ≦３
（７）
2023＝７×17×17と素因数分解が提供されている。
2023を割り切れる自然数⇒2023の約数。
素因数から2023の約数は【１、７、17、７×17、17×17、７×17×17】
2023の次に大きいのは、17×17＝289
（８）
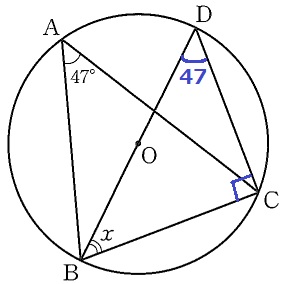
直径に対する円周角→∠ＤＣＢ＝90°
弧ＢＣの円周角→∠ＢＤＣ＝47°
△ＢＣＤの内角で、ｘ＝180－（47＋90）＝43°
（９）
回転体は半径３ｃｍの半球。
【円の体積Ｖ＝４/３πｒ3】
４/３π×３3÷２＝18πｃｍ3
（10）
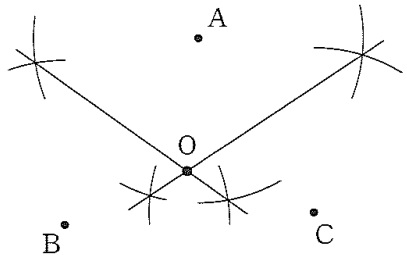
３点を通る円の中心Ｏの作図。
ＡＢ、ＢＣ、ＣＡ、いずれか２本の垂直二等分線の交点がＯ。
大問２（小問集合２）
問１（１）
12個の中央値は６番目と７番目の平均。
14と14の平均→14冊
（２）
①第１四分位数は下位６個の真ん中、下から３番目と４番目の平均で11.5冊。×
②最頻値（モード）は最もあらわれている値で14冊と17冊。×
③四分位範囲＝第３四分位数－第１四分位数＝17－11.5＝5.5冊〇
④（９＋10＋11＋12＋13＋14＋14＋16＋17＋17＋20＋21）÷12
＝174÷12＝14.5冊×
③
（３）
最大値21冊→①×
中央値14冊→②×
第１四分位数11.5冊→③×
④
問２（１）
４個中１個だから、確率は１/４。
（２）
１回目で４以外を出す→確率は３/４
２回目で残った３個から４を出す→確率は１/３
３/４×１/３＝１/４
（３）
ルールを確認する。
①１回目＜２回目→２回目を４にする。
②１回目＞２回目→３回目を４にする。
１回目と２回目の取り出し方のみ考える。
全体は４×４＝16通り
①（１回目、２回目）＝（１、４）（２、４）（３、４）
②最初の２回は４を出さない。３回目で４を出す予定にする。
（１回目、２回目）＝（２、１）（３、１）（３、２）
合計６通り。
確率は６/16＝３/８
問３
「ｎを整数とし、２つの続いた偶数のうち、小さいほうの偶数を２ｎとすると、」
大きいほうの偶数は２ｎ＋２となる。
２ｎ（２ｎ＋１）＋１
＝４ｎ2＋２ｎ＋１
＝（２ｎ＋１）2
ｎは整数だから、２ｎ＋１は奇数。
よって、題意は示された。
大問３（関数）
問１
ｙ＝１/４ｘ2にｘ＝－４を代入。
ｙ＝１/４×（－４）2＝４
問２
同様にＢ座標を出すと（２、１）
Ａ（－４、４）→Ｂ（２、１）
右に６、下に３だから、傾きは－３/６＝－１/２
問３（１）
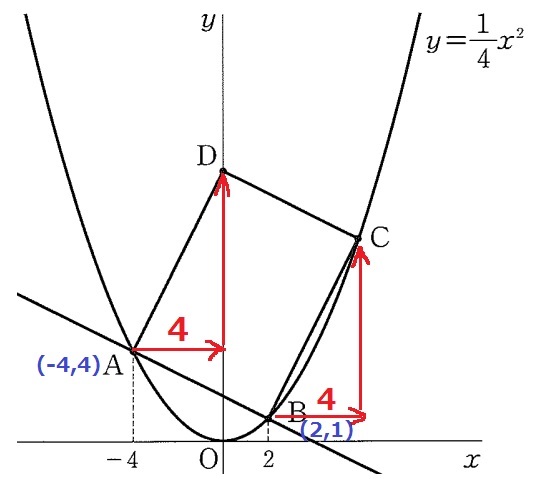
四角形ＡＢＣＤは平行四辺形。
ｘ座標だけを考える。
Ａから右に４でＤ。同様にＢから右に４でＣ。
Ｃのｘ座標は２＋４＝６
（２）
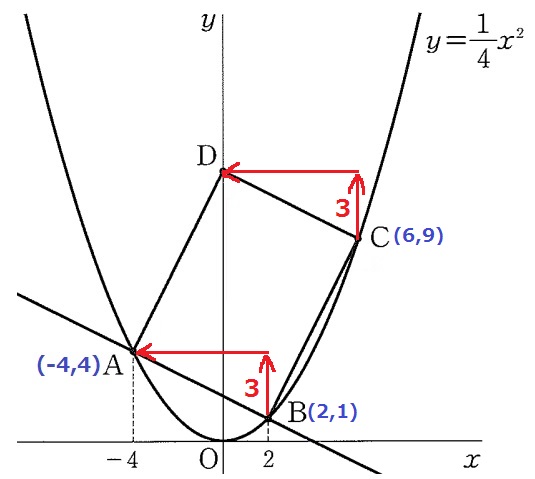
ｙ＝１/４ｘ2にｘ＝６を代入→Ｃ（６、９）
ｙ座標だけを考える。
Ｂから３上がってＡ。Ｃから３上がってＤ。
Ｄのｙ座標は、９＋３＝12
（３）
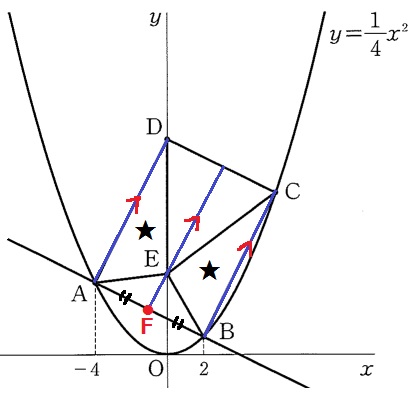
△ＡＤＥ＝△ＢＣＥ
平行四辺形の対辺は等しいので、ＡＤ＝ＢＣ
面積が等しく、底辺も等しい→高さも等しい。
Ｅを通るＡＤに平行な線をひき、ＡＢとの交点をＦとすると、
２つの三角形は高さが等しいから、３直線は等間隔に並ぶ→ＦはＡＢの中点。
Ｆ座標はＡ座標とＢ座標の平均で、Ｆ（－１、５/２）
Ａ（－４、４）→Ｄ（０、12）
右に４、上に８だから、ＡＤの傾きは２。
平行からＦＥの傾きも２。
Ｆから右に１、上に２移動して、Ｅのｙ座標は５/２＋２＝９/２
大問４（空間図形）
問１
２×２÷２×４÷３＝８/３ｃｍ3
問２
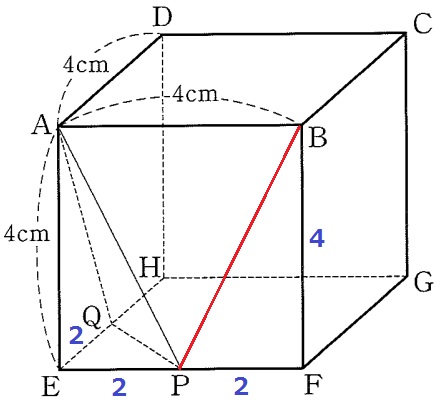
△ＥＰＱで三平方→直角二等辺の１：１：√２より、ＰＱ＝２√２ｃｍ
△ＢＰＦで三平方→ＢＰ＝２√５ｃｍ
ＰＱ＝２√２ｃｍ ＢＰ＝２√５ｃｍ
問３（１）
四角形ＢＤＱＰは等脚台形で左右対称。
ＲＳ＝ＰＱ＝２√２ｃｍ
ＢＲ＝（４√２－２√２）÷２＝√２ｃｍ
（２）
△ＢＲＰで三平方→台形の高さＲＰ＝３√２ｃｍ
（４√２＋２√２）×３√２÷２＝18ｃｍ2
（３）
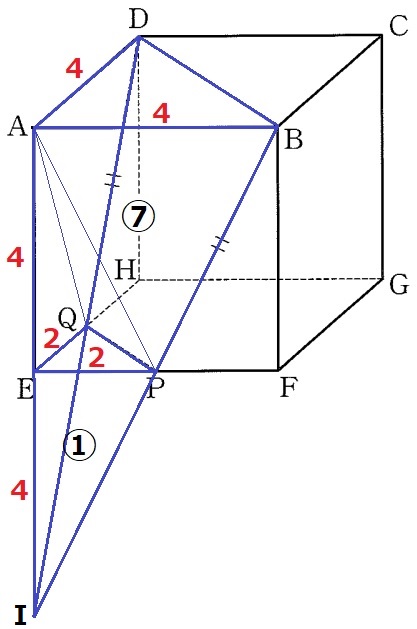
ＡＥ、ＢＰ、ＤＱを延長した交点をＩとする。
三角錐Ｉ―ＥＰＱ∽三角錐Ｉ―ＡＢＤの相似比は、ＥＰ：ＡＢ＝１：２
体積比は相似比の３乗、三角錐Ｉ―ＥＰＱ：三角錐Ｉ―ＡＢＤ＝①：⑧
求めるべき角錘台の体積は⑦に相当する。
よくみると、三角錐Ｉ―ＥＰＱ（①）は問１で求めた三角錘Ａ―ＥＰＱと合同なので、
８/３×⑦＝56/３ｃｍ3
問４
先ほどの立体の体積⑦から三角錘Ａ―ＥＰＱ（①）を引くと、
四角錘Ａ―ＢＤＱＰの体積は⑥である。
体積は、８/３×⑥＝16ｃｍ3
底面積の四角形ＢＤＱＰは問３（２）より18ｃｍ2。
高さＡＴの長さは、16×３÷18＝８/３ｃｍ
大問５（平面図形）
問１
長方形の対辺は等しい。ＥＣ＝３ｃｍ
ＢＥ＝６－３＝３ｃｍ
△ＡＢＥの面積は、３×４÷２＝６ｃｍ2
問２
△ＤＡＦ≡△ＢＥＦの証明。
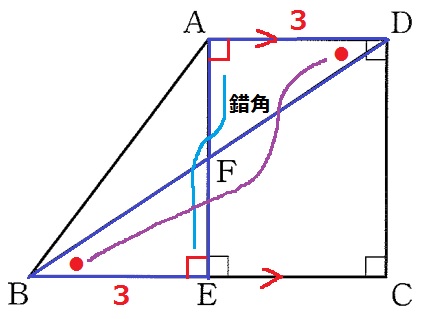
ＤＡ＝ＢＥ＝３ｃｍ
ＡＤ//ＢＣの錯角で、∠ＡＤＦ＝∠ＥＢＦ（●）
∠ＤＡＦ＝∠ＢＥＦ＝90°
１辺と両端角が等しいから合同。
ア…錯角、イ…１辺と両端角
問３（１）
ＰＱを折り目（対称の軸）としてＢとＤは対応する点。
ＢＤ⊥ＰＱだから∠ＰＦＢ＝90°
△ＰＢＦの内角より∠ＢＰＦ＜90°なので、∠ＡＰＦ＞90°
△ＦＰＡは直角三角形ではなく、△ＤＡＦと相似ではない。
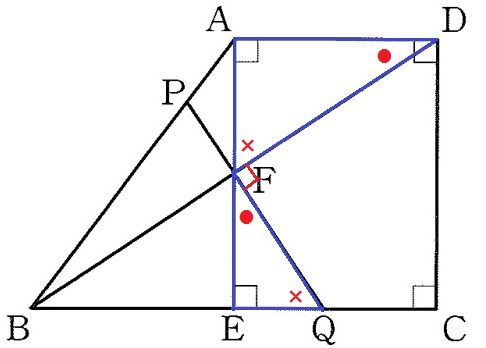
∠ＡＤＦ＝●、∠ＤＦＡ＝×とする。
∠ＤＦＱ＝90°、●＋×＝90°から∠ＥＦＱ＝●
２角相等で△ＤＡＦ∽△ＦＥＱ
前問の△ＤＡＦ≡△ＢＥＦより、ＡＦ＝ＦＥ＝４÷２＝２ｃｍ
ＢＥ：ＥＡ＝３：４、ＦＡ：ＡＤ＝２：３
２辺の比が異なるので、△ＡＥＢと△ＤＡＦは相似ではない。
また、線対称から∠ＰＢＦ＝∠ＰＤＦ＜∠ＦＤＡ
△ＤＡＦと△ＢＦＰは２角が異なり、相似ではない。
②
（２）
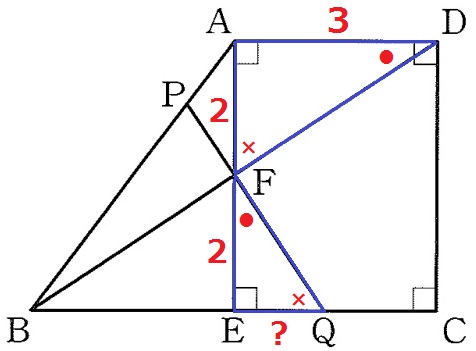
△ＤＡＦ∽△ＦＥＱより、ＤＡ：ＡＦ＝ＦＥ：ＥＱ＝３：２
ＥＱ＝２×２/３＝４/３ｃｍ
（３）
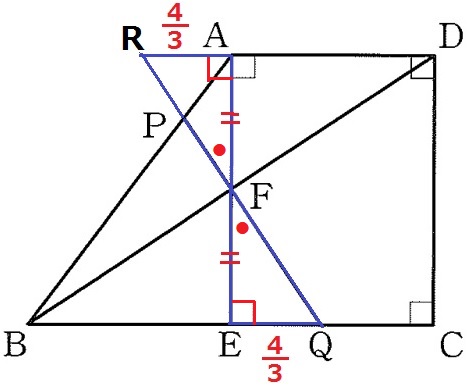
問２の△ＤＡＦ≡△ＢＥＦから、ＡＦ＝ＥＦ
ＤＡとＱＰを延長、交点をＲとする。
１辺と両端角が等しく△ＡＲＦ≡△ＥＱＦ→ＡＲ＝ＥＱ＝４/３ｃｍ
△ＡＲＰ∽△ＢＱＰより、ＡＰ：ＰＢ＝ＡＲ：ＢＱ＝４/３：13/４＝４：13
大問６（規則）
問１
【１、４、８、12、16…】
２番目以降は４個ずつ増えているので、６段目は20個（ア）
＠余談＠
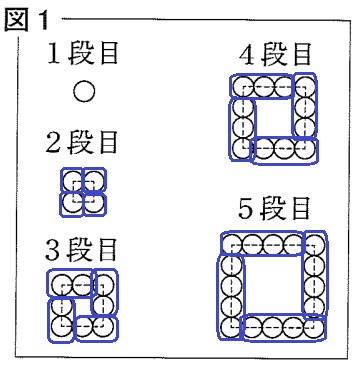
なぜ４個ずつ増えるのか、魔方陣で考えるといい。
１つの固まりが１個ずつ増えるので、計４個ずつ増えていく。
６段目までの和は、１＋４＋８＋12＋16＋20＝61個（イ）
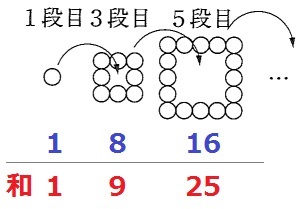
１つ前の奇数段目を正方形の中にいれると、ちょうど正方形が埋まる。
１段目までの和―１個
３段目までの和―３×３＝９個
５段目までの和―５×５＝25個
39段目までの和は39の平方数（ウ）
偶数段目も同様にできるという。
試しに計算してみると、
２段目までの和―２×２＝４個
４段目までの和―４×４＝16個（＝４＋12）
６段目までの和―６×６＝36個（＝４＋12＋20）
40段目までの総和
＝39段目までの奇数段目の和＋40段目までの偶数段目の和
＝39×39＋40×40＝3121個（エ）
ア…20、イ…61、ウ…39、エ…3121
問２
真ん中の穴を埋められる組み合わせを見つける。
オ…１段目と４段目、カ…２段目と５段目、キ…３段目と６段目
問３
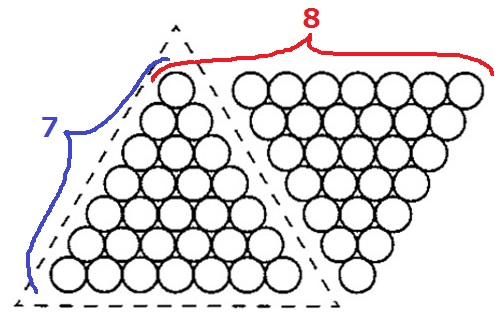
正三角形の１辺は７個。図は７段目までを示している。
同じ正三角形を点対称に並べて平行四辺形をつくる。
これを÷２にすればいい。
７×（７＋１）÷２
ク…７、ケ…２
問４
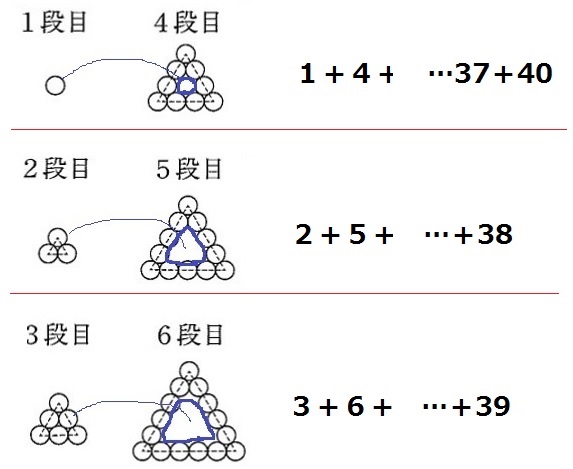
問４で３組に分けると、それぞれの正三角形が埋まった。
40を３で割ったときの余りでグループ分けする。
終わり数は余り＋１のグループが40、余り＋２のグループが38、余り０のグループが39。
⇒１辺が38、39、40である３つの正三角形の合計が答えになる。
求め方は問３の解法に倣う。
38×39÷２＋39×40÷２＋40×41÷２
＝（38×39＋39×40＋40×41）÷２
＝｛1482＋（39＋41）×40｝÷２
＝（1482＋3200）÷２
＝2341個
コ…2341
＠別解＠
【１、３、６、９、12…】
最初が１で、２番目から３の倍数が続く。
最後の数は39番目の３の倍数である。
１＋３×（１＋２＋３…＋39）
＝１＋３×｛（１＋39）×39÷２｝
＝2341個
小問数が多く、前半は手堅く稼いでおきたい。
後半の誘導にもなっているので間違えられない。
大問１
（６）右下の一次関数だから、ｘ＝－１がｙの最大値。
（７）2023の約数のうち、2023の１つ下が答えになる。
（８）直径ＢＤに対する円周角を見る。
大問２
問１：データの活用は基礎レベルで判断しやすかった。
問２（３）まずルールを把握する。
３回取り出すが、１回目と２回目の取り出し方で決着できる。
「３回目で４を出す」は「１回目と２回目で４を出さない」でクリア。
大問３
問３（１）（２）この操作は公立入試の世界で見かける。
（３）ＡＤとＢＣの真ん中の直線上にＥがあると見抜けるか。
大問４
問４：ここも前の小問が誘導になっている。
体積は体積比から計算すると求めやすい。
大問５
問３（１）なぜ他の三角形は△ＤＡＦと相似ではないのか、確認しておきたい。
（２）問２の合同からＦはＡＥの中点。
（３）平面のラス問では取りやすい部類にはいる。
ＡＰ、ＰＢを１辺とする三角形の相似を見つける。
大問６
まとまった問題文ゆえ、時間配分をミスると完走が難しくなる。
問１ｳｴ：図をよく観察すること。
問２：図３の並びがありがたい。
問３：クは正三角形の１辺の個数。
等差数列の和の公式は小学生でも理解できるものだが、
公立高校入試では禁忌なのか、小問として出題された。
問４：誘導にのらない方が早い(;^ω^)
記述問題ではないので良いかと。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント