平均59.5点（前年比；＋1.8点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）①
２－（－４）
＝２＋４
＝６
②
６ａ2×１/３ａ
＝２ａ3
③
－２（３ｘ－ｙ）＋２ｘ
＝－６ｘ＋２ｙ＋２ｘ
＝－４ｘ＋２ｙ
（２）①
６ｘ－１＝４ｘ－９
２ｘ＝－８
ｘ＝－４
②
ｘ2＋５ｘ＋３＝０
解の公式を適用して、ｘ＝（－５±√13）/２
（３）
絶対値…数直線上で原点０との距離。
分数は小数に直すと絶対値は、ア：３、イ：５、ウ：2.5、エ：2.1。
絶対値が最も小さいのはエ。
（４）
ｙ＝ａｘ2に（－２、－12）を代入。
－12＝４ａ
ａ＝－３
（５）
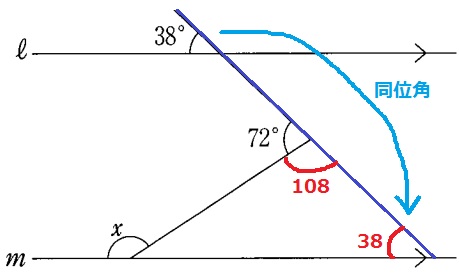
同位角で38°をおろす。
180－72＝108°
外角定理で、ｘ＝108＋38＝146°
（６）
答案には求める過程も記述する。
ａ2－４ａ＋４
＝（ａ－２）2 ←ここで代入。
＝｛（２＋√５）－２｝2
＝５
（７）
１枚目のカードは戻さない。33や44は無い。
32以上は32・34・41・42・43の５通り。
２枚のカードを引く場合の数は、４×３＝12通り
確率は５/12
（８）
ＡＢを立方体の高さにおいて組み立ててみる。
ＡＢは天井のアと底面のカに対して垂直になる。
ア・カ
（９）
ア：最小値は35回。最小値が複数人の場合もある。×
イ：最大値は95回。〇
ウ：平均値を×印などで示す箱ひげ図もあるが、本問にはないので不明。×
57回は中央値（第２四分位数）である。
エ：15人の中央値は８番目の値で57回。
60回以下は少なくとも８人いるが、９人いるとは確実にいえない。×
上から７番目（下から９番目）が61回かもしれない。
オ：15人の第１四分位数は上位７人の真ん中、上から４番目。
第１四分位数が66回あたりなので、少なくとも４人以上は60回以上である。〇
イ・オ
大問２（関数）
（１）①
一次関数；ｙ＝ａｘ＋ｂの変化の割合は傾きａで一定。
〇
②
ｙ＝ａｘ2は変化の割合が一定ではない。
×
（２）
ア：ｙ軸について対称→左右対称。反比例は原点について点対称。
イ：反比例はｘ軸にもｙ軸にも交わらない。
ウ：ｘ＝１を代入してｙの値を求める。
エ：反比例だけ減少。
イ・エ
大問３（規則）
（１）
ａ、５、ｂ…を１周とする。
20÷３＝６…２
20番目は６周＋２。余り２だから５。
（２）
答案では求める過程も書く。
７÷３＝２周…１
２（ａ＋５＋ｂ）＋ａ＝18
３ａ＋２ｂ＝８ …①
50÷３＝16周…２
16（ａ＋５＋ｂ）＋ａ＋５＝121
17ａ＋16ｂ＝36 …②
①と②の連立を解いて、
ａ＝４、ｂ＝－２
大問４（平面図形）
（１）
△ＡＢＤ≡△ＣＤＢの証明。
平行四辺形の対辺＋共通辺→３辺
平行四辺形の対辺＋対角→２辺夾角
２つの錯角＋共通辺→１辺両端角
（２）
事柄の逆が成り立たない、反例となる図形を作図する。
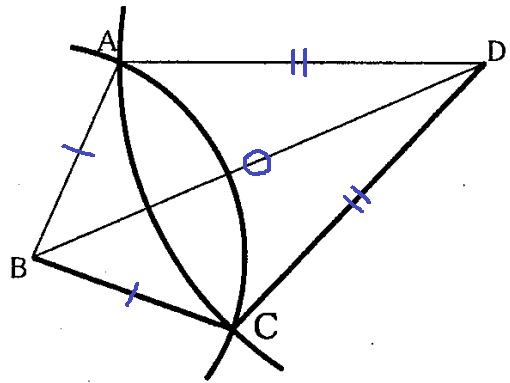
△ＡＢＤと△ＣＢＤは３辺が等しく合同であるが、四角形ＡＢＣＤは平行四辺形ではない。
ＢＤに対して線対称な図形をつくればいい。
＠逆・裏・対偶＠
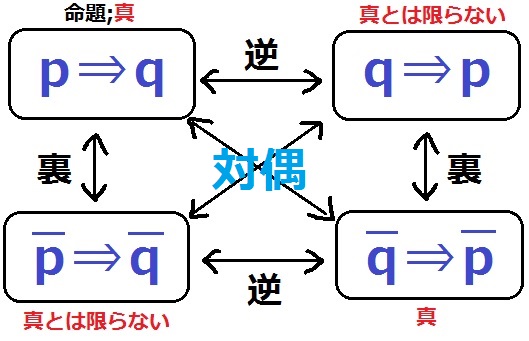
『ｐであるならば、ｑである』という命題に対して、
『ｑであるならば、ｐである』を逆といい、
『ｐでないならば、ｑではない』を裏という。（ｐやｑの上に￣がつく）
逆や裏は必ずしも真とは限らない。
『ｑでないならば、ｐではない』を対偶といい、
元の命題（ｐ⇒ｑ）が真ならば、対偶は必ず真である。
たとえば、【４の倍数であれば、２の倍数である】という真の命題に対して、
逆【２の倍数であれば、４の倍数である】、
裏【４の倍数でなければ、２の倍数でない】は反例があるので偽である。
（６や10は４の倍数ではない２の倍数）
一方で、対偶【２の倍数でなければ、４の倍数でない】は真である。
大問５（数量変化）
（１）
ｙ＝１/４ｘ2にｘ＝６を代入。
ｙ＝１/４×36＝９ｍ
（２）①
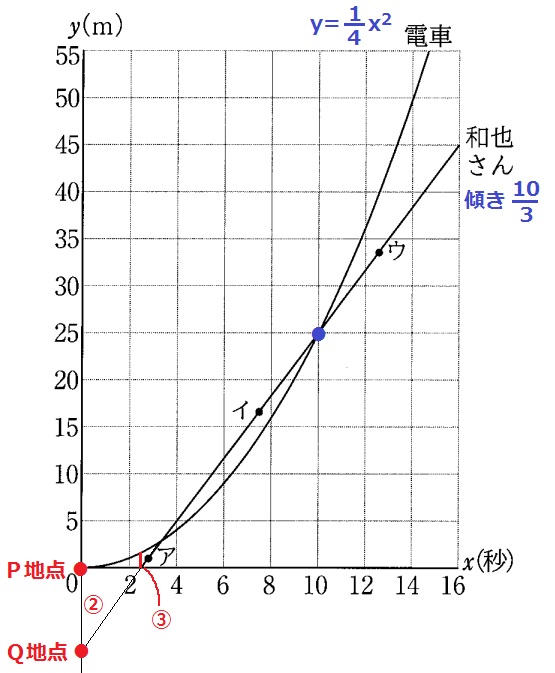
２つのグラフで上にくる方がＰ地点から遠くにいる＝前を走っている。
和也のグラフが電車より上にあるのはイ。
②
ｙ＝０がＰ地点。
Ｑ地点は和也のグラフを下に延長させた切片。
電車に追い越される10秒後まで、和也は10/３×10＝100/３ｍ走った。
電車の移動距離は25ｍ（Ｐ地点から25ｍ地点）だから、ＰＱの距離は100/３－25＝25/３ｍ
③
和也がＰ地点を走っていたときの和也と電車との距離、
すなわち、和也がｙ＝０のときの電車のｙ座標を求めればいい。
和也がＰ地点に着いた時間は、25/３ｍ÷秒速10/３ｍ＝５/２秒
ｙ＝１/４ｘ2にｘ＝５/２を代入。
ｙ＝１/４×25/４＝25/16ｍ
大問６（平面図形）
（１）
∠ＡＯＤ＝１/２∠ＥＯＦの証明。
半径よりＣＯ＝ＣＤ→△ＣＯＤは二等辺三角形。
∠ＥＤＦ＝∠ＡＯＤ …①
∠ＥＤＦは弧ＥＦの円周角で、円周角は中心角の半分だから、
∠ＥＤＦ＝１/２∠ＥＯＦ …②
①、②から∠ＡＯＤ＝１/２∠ＥＯＦ
ア…二等辺、イ…ＡＯＤ，ウ…中心
（２）①
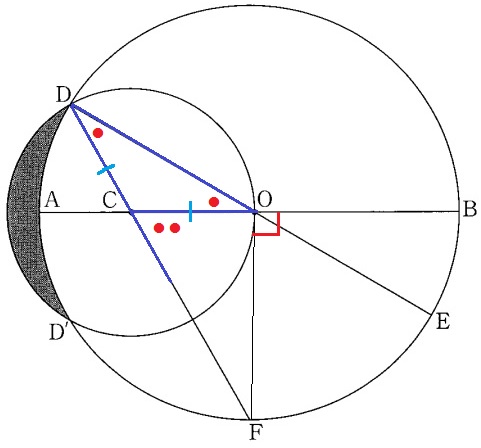
∠ＥＤＦ＝●とする。
△ＣＯＤは二等辺で、外角定理から∠ＯＣＦ＝●●
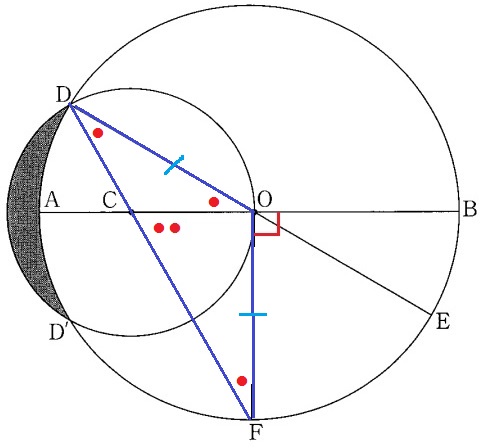
半径よりＯＤ＝ＯＦで、△ＯＤＦも二等辺三角形。
∠ＯＦＤ＝●
△ＯＣＦで外角定理→∠ＢＯＦ＝●●●＝90°
∠ＥＤＦ（●）＝90÷３＝30°
②
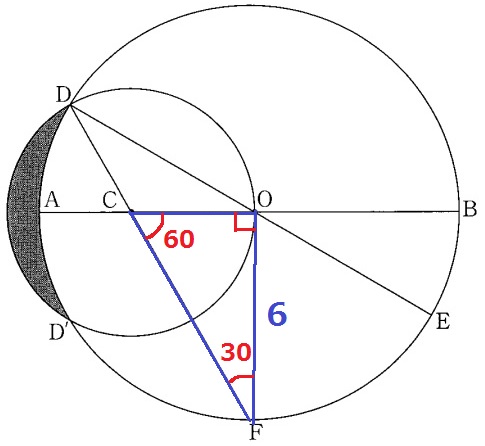
前図の●＝30°から、△ＯＣＦの内角は30°ー60°ー90°の直角三角形。
辺の比は１：２：√３だから、ＣＯ＝６×１/√３＝２√３ｃｍ
③
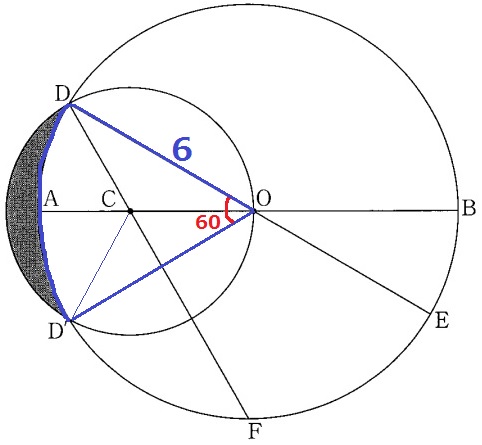
曲線ＤＤ’を対処するために、これを弧とする扇形ＯＤＤ’は必ず拾い上げなくてはならない。
①の図から∠ＤＯＣ（●）＝30°
小円の中心Ｃは大円の直径ＡＢ上にある→ＡＯを対称の軸として上下対称。
∠ＤＯＤ’＝30×２＝60°
扇形ＯＤＤ’の面積は、６×６×π×１/６＝６πｃｍ2
上図の部分から先ほどの扇形ＯＤＤ’を引けば、求積すべき図形の面積が求まる。
∠ＤＣＤ’はブーメランの３つの角の和で、30＋60＋60＝120°
小円の半径は２√３ｃｍだから、扇形ＣＤＤ’の面積は２√３×２√３×π×１/３＝４πｃｍ2
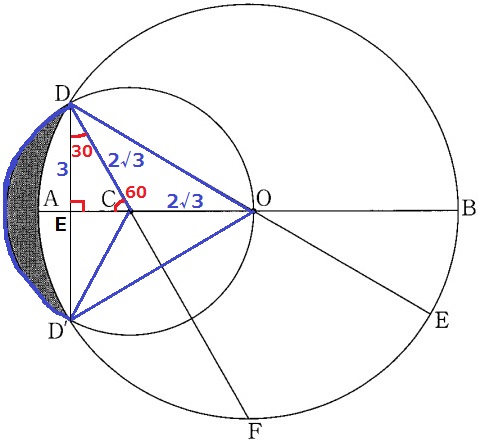
四角形ＯＤＣＤ’の面積を求める。
Ｄから垂線をひき、ＡＯの交点をＥとすると、△ＤＥＣの辺の比は１：２：√３。
ＤＥ＝２√３×√３/２＝３ｃｍ
△ＤＣＯは底辺ＣＯ＝２√３ｃｍ、高さＤＥ＝３ｃｍで、△Ｄ’ＣＯと合同だから、
四角形ＯＤＣＤ’の面積は、２√３×３÷２×２＝６√３ｃｍ2
よって、求積すべき図形の面積は、（４π＋６√３）－６π＝６√３－２πｃｍ2
＠＠
東京工業大学附属科学技術高校でこんな構図がでました(;´∀｀)
余力のある方は挑戦してみてください。
大問１
配点が40点もある。稼ぎどころ。
（７）カードを戻すか戻さないかをチェック。戻さないのでゾロ目はない。
（８）ＡＢと高さにする。カを底面、イウエオを側面、アを天井として組み立てる。
大問２
問題の形式が面白い。内容は基本レベル。
大問３
（２）基礎的な規則の問題だが、丁寧な立式が求められた。
大問４
平面と論理形式（逆）の融合だが、設問は解答しやすい。
（２）平行四辺形（図Ⅰ）以外の合同図形をつくる。線対称を想起。
大問５
②グラフでどこかＰＱ間の距離になるか。
和也の移動距離－電車の移動距離（25ｍ）で求まる。
③ここもグラフのどこを指すかを明確にする。
２問とも計算処理は複雑ではなかった。
大問６
（２）①∠ＥＤＦを何かの記号か文字に置き換えておく。
②①ができれば、ほぼ正答できる。
③群馬によくでてくる形式。まず、ＤＤ’を弧とする扇形を捉える。
（求める部分＋扇形ＯＤＤ’）－扇形ＯＤＤ’＝求める部分
合わせた図形を別の図形で分割する。有名三角形を利用する。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント