問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
９＋４×（－２）
＝９－８
＝１
（２）
５/11÷（－２/３）
＝－15/22
（３）
３ｘ＋２ｙ＝－５ …①
－ｘ＋３ｙ＝９ …②
①＋②×３をすると、11ｙ＝22
ｙ＝２
②に代入、－ｘ＋３×２＝９
ｘ＝－３
ｘ＝－３、ｙ＝２
（４）
（√６＋２）（√６－３）
＝６－３√６＋２√６－６
＝－√６
（５）
ｙ＝ａｘ2に（ｘ、ｙ）＝（６、12）を代入。
12＝36ａ
ａ＝１/３
ｙ＝１/３ｘ2
（６）
多角形の外角の和は360°。
正多角形の場合、外角はどこも同じ大きさである。
外角の数は360÷40＝９個
正九角形だから辺の数は９本。
（７）
三平方の定理で、ＡＣ2＝７2－４2＝33
ＡＣ＞０だから、ＡＣ＝√33ｃｍ
（８）
抽出した35個のうち、白：黒＝21：14＝③：②
全体は450個だから、黒は450×②/⑤＝180個
ア
大問２（小問集合２）
（１）
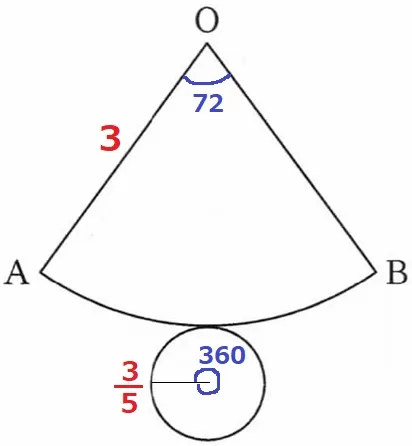
中心角の比は、扇形：円＝72：360＝①：⑤
母線：円の半径は逆比で⑤：①→円の半径は３×①/⑤＝３/５ｃｍ
表面積は、３/５×３/５×π＋３×３×π×１/５＝54/25πｃｍ2
（２）
６段目にいるには、和が６か10になればいい。
●和が６
（１、５）（２、４）（３、３）（４、２）（５、１）の５通り。
●和が10
（４、６）（５、５）（６、４）の３通り。
計８通りで全体は６×６＝36通りだから、確率は８/36＝２/９
（３）
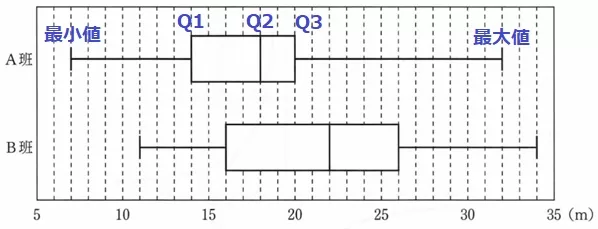
ア：平均値を×印などで示す箱ひげ図もあるが、本問は不明。×
Ａ班の18ｍは中央値（Q2）である。
イ：23人の中央値は12番目の値。
第１四分位数（Q1）は下位11人の真ん中、下から６番目。
Ｂ班の下から６番目が16ｍなので、少なくとも１人はいる。〇
ウ：範囲＝最大値－最小値。ヒゲ～ヒゲの長さで、Ａ班の方が大きい。×
エ：四分位範囲＝Q3－Q１。箱の長さはＢ班の方が大きい。〇
オ：Ｂ班の中央値が22ｍなので、22ｍ以上は少なくとも12人いる。
対して、Ａ班のQ3から上から６番目が20ｍ。22ｍ以上は多くても５人。
22ｍ以上はＢ班がＡ班の２倍以上いる。〇
イ・エ・オ
大問３（関数）
（１）
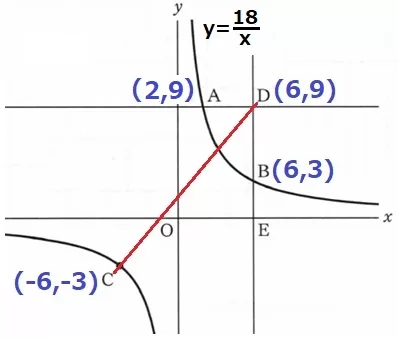
ｙ＝18/ｘに代入して、各座標を調べる。
Ａ（２、９）Ｂ（６、３）Ｃ（－６、－３）
Ｄのｘ座標はＢ、ｙ座標はＡと同じ→Ｄ（６、９）
Ｃ（－６、－３）→Ｄ（６、９）
右に12、上に12だから、傾きは12/12＝１
Ｃから右に６、上に６移動して、切片は－３＋６＝３
ｙ＝ｘ＋３
（２）
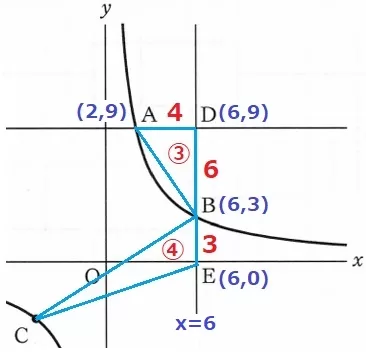
△ＡＢＤの面積は、６×４÷２＝12
△ＢＣＥの面積は仮定より、12×④/③＝16
底辺をＢＥとしたときの高さは、16×２÷３＝32/３
Ｃのｘ座標はｘ＝６から左に32/３離れている。
６－32/３＝－14/３
大問４（平面図形）
△ＡＥＦ≡△ＡＧＦの証明。
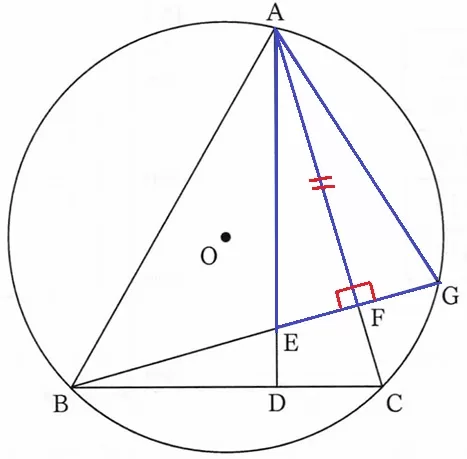
仮定からＡＣ⊥ＢＧなので、∠ＡＦＥ＝∠ＡＦＧ＝90°
共通辺ＡＦ。ここまでは見えやすい。
半径もなく、辺の情報が乏しいので両端角に絞る。
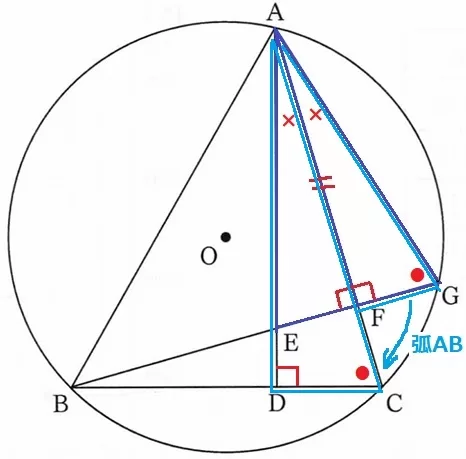
弧ＡＢの円周角より、∠ＡＣＤ＝∠ＡＧＦ（●）
△ＡＤＣの内角から、∠ＥＡＦ＝90－∠ＡＣＤ（●）
△ＡＦＧの内角から、∠ＧＡＦ＝90－∠ＡＧＦ（●）
∠ＥＡＦ＝∠ＧＡＦ（×）
以上より、１辺と両端角が等しいから合同。
大問５（数量変化）
（１）
関数の定義。かつての学テで正答率が低かった。
借りた時間ｘが決まると、料金ｙ円が決まる。
『ｘの値を決めると、それに応じてｙの値がただ１つに決まるから』
ｙはｘの関数といえる。
＠＠
逆に料金ｙ円が決まっても、借りた時間ｘは１つに決まらないので、
『ｘはｙの関数ではない』
（２）
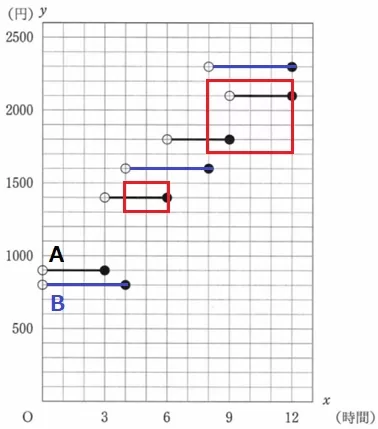
青線がＢ。Ａに倣い、〇（含まない）―●（含む）の順に記す。
Ａ＜Ｂの判断は縦方向で見る。４～６時間と８～12時間はＡの方が安い。
ア…４、イ…６
大問６（整数）
（１）
連続する３つの整数は、ｎ、ｎ＋１、ｎ＋２。
中央の数を２乗して３倍した数なので、最終的に３（ｎ＋１）2に持っていく。
—–
ｎ2＋（ｎ＋１）2＋（ｎ＋２）2－２
＝ｎ2＋（ｎ2＋２ｎ＋１）＋（ｎ2＋４ｎ＋４）－２
＝（３ｎ2＋６ｎ＋５）－２
＝３ｎ2＋６ｎ＋３
＝３（ｎ2＋２ｎ＋１）
＝３（ｎ＋１）2
ｎ＋１は連続する３つの整数の中央の数だから、
３（ｎ＋１）2は中央の数を２乗して３倍した数である。
（２）
先ほどの式から、連続した３つの整数を２乗した和は３ｎ2＋６ｎ＋５だった。
ｎ2＋（ｎ＋１）２＋（ｎ＋２）2－５
＝（３ｎ2＋６ｎ＋５）－５
＝３ｎ2＋６ｎ
＝３ｎ（ｎ＋２）
ｎは最も小さい数、ｎ＋２は最も大きい数。
３ｎ（ｎ＋２）は最も小さい数と最も大きい数の積を３倍した数。
ア…⑤、イ…３
（３）
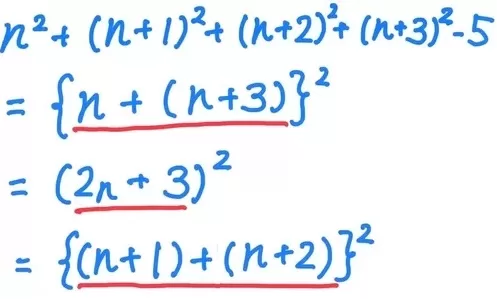
『連続する４つの整数をそれぞれ２乗した和から５をひいた数』
→ｎ2＋（ｎ＋１）2＋（ｎ＋２）2＋（ｎ＋３）2－５
これが『最小数と最大数の和の２乗に等しい』ので、
展開して計算する必要はなく、｛ｎ＋（ｎ＋３）｝2になる。
カッコ内の数字だけを変える。
｛ｎ＋（ｎ＋３）｝2＝（２ｎ＋３）2＝｛（ｎ＋１）＋（ｎ＋２）｝2
（＊定数項を３＝１＋２に分ける）
小さい方から２番目の数（ｎ＋１）と大きい方から２番目の数（ｎ＋２）の和を２乗した数。
③
上位校が抜ける試験でもないのに易問が多い。
数学が得意な子は他教科で稼がねばならない。
大問１
いずれも基本問題。ケアレスミスに注意！
（６）正多角形ではない多角形の外角は同じ大きさではない。
（８）抽出した35のうち黒は14個。この割合は母集団も同じとみなす。
大問２
取りやすい。
（１）中心角の比、母線：半径の比は逆比である。
（３）オ：22ｍ以上はＡが４分の１いない、Ｂが過半数→ＢはＡの２倍以上いる。
大問３
方針は立てやすい。
（２）△ＡＢＤが求めやすい。処理も複雑ではない。
大問４
∠ＥＡＦ＝∠ＧＡＦをどう指摘するか。
いくつか方法があるが、わかりやすいのはそれぞれを内角とする△ＡＤＣと△ＡＦＧを使う。
大問５
計算すらなく、時間がかからない。
（１）盲点だが、中１の範囲。
（２）Ａのように記すだけ。ＡがＢの下にくる範囲がＡが安いとき。
大問６
（１）それを証明するにはどのような式に変形すればいいか。
あらかじめ想定しておく。
（３）連続する４つの整数に変わるが、性質Ⅱから形が判明している。
カッコの中身をいじくるだけ。計算力より読解力だろうか。。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント