平均26.3点(前年比;+1.6点)
最高点―50点、最低点―0点
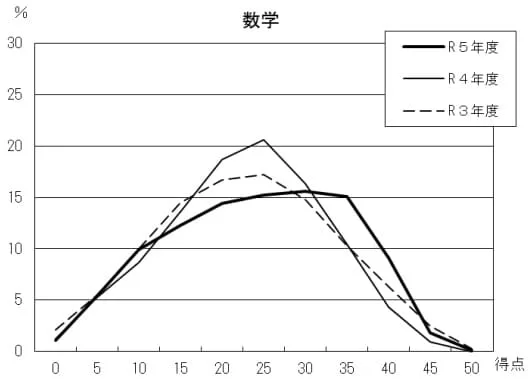
問題はこちら→リセマムさん
大問1(小問集合)
(1)
2+12÷(-3)
=2-4
=-2
(2)
√20+10/√5
=2√5+2√5
=4√5
(3)
x2+x-4=0
解の公式を適用して、x=(-1±√17)/2
(4)
鉛筆5本…5a円、ボールペン3本…3b円
合計が1000円より高い。
5a+3b>1000
(5)
弧BCに対する円周角より、∠BAC=24°
外角定理を使って、x=48+24=72°
(6)
x座標の差は2、y座標の差は3。
三平方の定理で距離は√13。
(7)
ア:y=2πx(比例)
イ:y=πx2(y=ax2)
ウ:2(x+y)=20→y=-x+10(一次関数)
エ:xy=20→y=20/x(反比例)
エ
(8)
3問解く日をxとすると、5問解く日は20-x
3x+5(20-x)=70
2x=30
x=15日
20-15=5日
3問解く日…15日、5問解く日…5日
②
bc-ad
=(n+7)(n-1)-(n-7)(n+1)
=(n2+6n-7)-(n2-6n-7)
=12n
nは自然数だから、12nは12の倍数。
ア
大問2(確率・空間図形)
(1)①
赤は4個中3個だから、確率は3/4。
②
1回目で赤を取る。
残りの赤は3個中2個。
2個とも赤の確率は、3/4×2/3=1/2
③
1回目、2回目ともに赤を出す確率は3/4。
2個とも赤の確率は、3/4×3/4=9/16
(2)①

ネジレの位置→平行ではない、かつ延長しても交わらない。
正四面体の展開図で、端の3点(●)はくっついて交わる→ア~ウは×!
エを組み立てると、ABとYXは平行ではなくなる。
エ
②
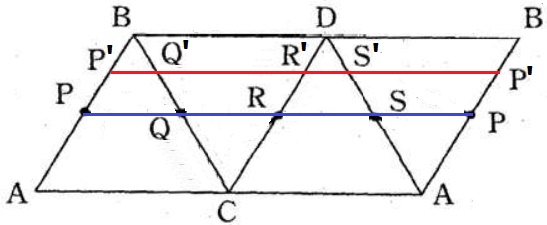
PQ+QR+RS+SPが最小になる→最短距離、これらの点が一直線上にあるとき。
P’も同様。全体は平行四辺形で対辺の長さは等しい→青線も赤線も長さが同じ。
Ⅰ…1つの直線上にある、Ⅱ…イ
大問3(データの活用・数量変化)
【2】
ア:Aの第1四分位数~第3四分位数。
下から25~75%のデータ、つまり全データの約半分。×
(Q1は下から13番目、Q3は38番目。少なくとも26台はある)
イ:BのQ1は下から13番目の値で、これが9000円。〇
ウ:Cの最小値が10500円位なので、10000円以下はない。〇
エ:×印などで平均値を記す箱ひげ図もあるが、本問にはない。×
イ・ウ
(2)①【1】
①の9000~10000円の度数は8台。
相対度数は8/50=16/100=0.16
【2】
②の9000~10000円の度数は6台→①の方が多い。
Q1は下から13番目→①9000~1万円、②8000~9000円。②がA店。
イ
(2)①
仮定より、『0≦x≦40のとき、yをxの一次関数とみなす』
(5、200)→(20、500)
右に15、上に300だから、傾きは300/15=20
切片は(5、200)から左に5、下に5×20=100移動して、200-100=100
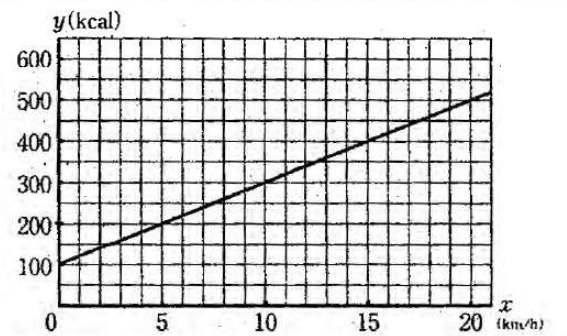
(0、100)(5、200)(20、500)を通過する直線をひく。
②
先のとおり、y=20x+100
③
前問の式にy=740を代入する。
740=20x+100
x=32
32km/h
大問4(関数)
(1)
y=1/2x2にx=-2を代入→A(-2、2)
Bはy軸についてAと対称だから、B(2、2)
AB=2-(-2)=4
(2)①
いずれの選択肢もxの増加量は2。
原点Oから離れるほどyの増加量が増える。
変化の割合が最も大きいのはウ。
②
y=1/2x2は下に凸のグラフで、xの変域は原点を通過する。
x=0のとき、最小値y=0
x=-3のとき、最大値y=9/2
0≦y≦9/2
(3)①
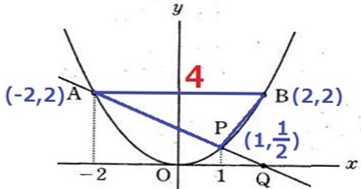
P(1、1/2)
△APBの底辺AB=4、高さは2-1/2=3/2
面積は、4×3/2÷2=3
②【1】
y=1/2x2にx=4を代入→P(4、8)
A(-2、2)→P(4、8)
右に6、上に6だから、傾きは6/6=1
【2】
QはA(-2、2)から下に2、左に2移動して、x座標は-2-2=-4
Q(-4、0)
③
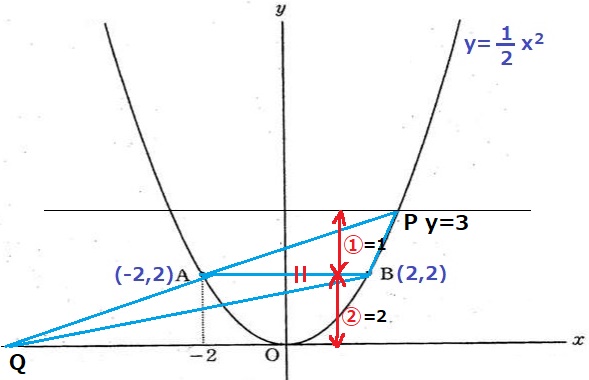
△APB=△AQB×1/2
いずれも底辺ABが共通辺→△APBと△AQBの高さの比が①:②
Bのy座標から②=2→①=1、Pのy座標は3。
y=1/2p2にy=3を代入。
3=1/2p2
p2=6
p>0だから、p=√6
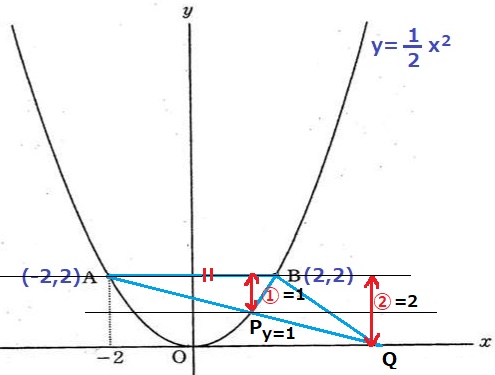
もう1つは、PがABより下にあるパターン。
Bのy座標から②=2→①=1、Pのy座標は1。
y=1/2p2にy=1を代入。
1=1/2p2
p2=2
p>0だから、p=√2
p=√2、√6
大問5(平面図形)
(1)①
折り返し→CDを対称の軸とする対称移動。
△A’CD
②
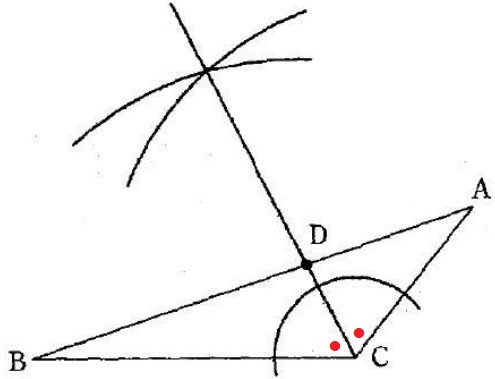
答案用紙にはA’がない。
CDが対称の軸となる→対応する角は等しいから∠ACD=∠BCD(∠A’CD)
∠ACBの二等分線をひき、ABとの交点がDとなる。
(2)①
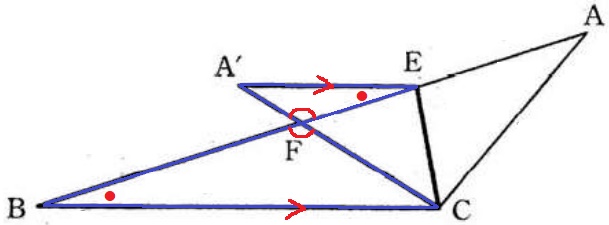
対頂角+A’E//BCの錯角で2角相等→△A’FE∽△CFB
②
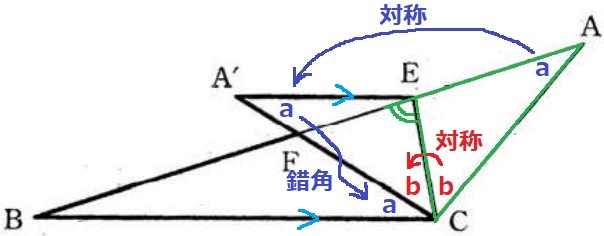
aとbを対称移動。さらにaを錯角で移動。
∠BCE=a+b
△AECで外角定理を適用すると、∠BEC=a+b
∠BCE、∠BEC
③
前問を利用する。
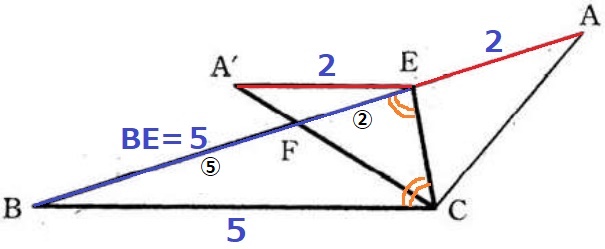
∠BCE=∠BECから△BCEは二等辺三角形→BC=BE=5cm
AE=A’E=7-5=2cm
△A’FE∽△CFBより、BF:EF=⑤:②
EF=5×②/⑦=10/7cm
(3)

60°が有名角。角度を調べて何か使えないか探る。
∠A’CG=∠ACG=90-60=30°
∠CA’G=∠CAG(●)の大きさはわからず、使えにくい。
GCを1辺とする三角形は△BCG。BCを伸ばしてみると…。

AからBCの延長線に垂線をおろし、足をHとする。
∠ACH=90-30=60°
△ACHの内角は30°―60°―90°→辺の比は1:2:√3
CH=3/2cm、AH=3√3/2cm
△BCG∽△BHA(2角相等)で、GC:AH=BC:BH=5:13/2=⑩:⑬
GC=3√3/2×⑩/⑬=15√3/13cm
●講評●
大問1
満点50点のうち、配点11点。
(8)までは完答したい。
(9)a~dの値をnを用いて正確に表す。
大問2
(1)確率は基本レベル。
(2)①交わったらネジレではない→展開図を組み立てて辺がくっついたらネジレではない。
②正四面体の展開図が平行四辺形である点に注目する。一直線が上にズレるだけで長さは等しい。
大問3
取りやすい設問であった。
大問4
小問数は多いが、基本レベルで計算処理もしやすい。
(3)③△APBと△AQBはABが共通辺で位置が決まっている。
Pは放物線上の点。APとx軸との交点がQ。
Pの下にQがあり、Pの位置が決まるとQの位置も自動で決まる。
→PがABより上か下かで2通り。
大問5
(2)③前問の活用。△BCEが二等辺と気づきたい。
(3)斜辺BGが出しにくい。∠A’CB=60°から反対側も60°
外側に直角三角形をつくると、CGに対応する辺がつくれる。





コメント