2016年度　茨城県公立高校入試問題過去問【数学】解説

平均48.9点
図形が難所。ラストは角の二等分線を利用。
データの活用も鍛えておく。
問題はコチラから→ＰＤＦファイル

大問１（計算）

（１）２－１１＝－９

（２）（－５）×（－３）＋（ー２）²÷４
＝１５＋１＝１６

（３）５/６＋（－４/９）÷４/３
＝５/６－１/３＝１/２

（４）３（2ｘ＋ｙ）－５（ｘ＋ｙ）
＝６ｘ＋3ｙｰ５ｘ－5ｙ
＝ｘ－２ｙ

（５）√２×√６＋３/√３
＝２√３＋√３＝３√３

大問２（小問集合）

ここも全問正解したい。大問１と２だけで４０点も稼げる。
（１）因数分解
ｘ²＋８ｘ＋１６＝（ｘ＋４）²

（２）連立方程式
代入法でも加減法でも。ｘ＝－１、ｙ＝１

（３）解の公式
ｚ＝（－７±３√５）/２

（４）不等式
ａが個数で、ｂが値段になっている。
300ａ＋7ｂ≦２５００

（５）代入
因数分解してから代入する。
ｘ²－ｘｙ＝ｘ（ｘ－ｙ）
(３＋√３)（３－√３）＝９－３＝６

大問３（小問複合２）

（１）１３５°
∠ＡＯＣ＝９０°、反対側が２７０°。
∠ＡＢＣは、この円周角なので、２７０÷２＝１３５°

（２）７３
２けたの自然数の十の位の数をｘとおく。
１０ｘ＋３＝２（３０＋ｘ）－１
ｘ＝７→２けたの自然数は７３。

（３）６/２５
全体は５×５＝２５通り。
素数は２、３、５だけ。
１は素数ではない！→（１、１）は除外
また、１以外のカードを２枚かけた積は素数ではなくなる。
よって、（１、２）（１、３）（１、５）とこれらの逆→６通り。
したがって、６/２５

大問４（関数）

（１）ｙ＝－ｘ＋２
*Ａ（２、０）、Ｂ（－２、４）を通る直線の式を求める。
右に４いって、下に４だから傾き－１。

（２）Ｐ（０、２√３）
*Ｃ（－６、０）
Ａ・Ｂ・Ｃが円周上にくるので、とりあえず中心点がどこか探す。
３点が通る円の中心は、作図でもでてくる通り、各辺の垂直二等分線が交わる場所。
それをヒントに調べると、ＡＣの中点、しかもＢの真下。半径４とわかる。
中心をＯとし、Ｏから半径４をｙ軸に向かって線を引く。
直角三角形ができる。三平方。４²－２²＝１２　→√１２＝２√３

大問５（相似）

（１）公式解答参照
*相似の証明。直角と対頂角が等しい＝２角が等しい→∽

（２）√２２
*△ＥＢＣに注目。∠ＡＢＣ＝４５°なので、直角二等辺三角形。よって、ＥＢ＝ＥＣ・・①
△ＦＥＢ△ＡＥＣに注目。仮定から、∠ＦＥＢ＝∠ＡＥＤ＝９０°・・②
前問の相似から、対応する角が等しいので、∠ＦＢＥ＝∠ＡＣＥ・・③
①、②、③より、一辺と両端角が等しい→△ＦＥＢ≡△ＡＥＣ。
この合同関係に気づけるかどうか。
△ＦＥＢ内で三平方→ＦＥ＝√１１
合同から、対応する辺であるＡＥ＝√１１
△ＡＥＦ内で三平方、√２２

大問６（数量変化）

（１）５Ｌ
*文章題は情報整理がものをいう。
Ａ：１Ｌで排水。３Ｌになると毎分２Ｌで増加、１５Ｌで停止。
Ｂ：３Ｌで排水。３Ｌになると毎分２Ｌで増加、１５Ｌで停止。
ありがたいことにグラフが提供されているので、Ｂも書き込み。
５分後は５Ｌになるはず。

（２）１３分１２秒
*水の量が等しくなるときは、グラフの交点。
１２分後にＡが給水し始めるが、このときＢは１０分後から排水している。
１２分までＢは６Ｌ排水、Ｂ残り９Ｌ。ＡとＢの差は９－３＝６Ｌ（グラフで確認）
Ａ２Ｌで増加、Ｂ３Ｌ減少なので、１分で５Ｌずつ差が縮まる。
６÷５＝１．２分＝１分１２秒
１２分＋１分１２秒＝１３分１２秒

大問７（データの活用）

（１）ａ＝１４、ｂ＝５６
*初見だと本番で戸惑うので、いくつか類題を解いて慣れておこう。
範囲が８１→最大値－最小値＝８１
９５－８１＝１４、ａはｂより小さいので、ａが最小値１４。
ｂは平均を使う。平均６０を基準とすると、
－５－４６＋５－２１＋２１＋２８＋１２＋３５－２５＝＋４
平均を６０にならすには、－４をする。
よって、ｂ＝６０－４＝５６

（２）５７．５
*１０個の標本なので、メジアンは５番目と６番目の平均。
大きい順にならべると上から５つは、９４、７２、６９、６５、６０。
ヒストグラムをみると、６０以上が５つ、６０未満が５つ。
６０の下は５５か、ｃかｄが５６以上５９以下であればそちらになる。
しかし、ｃとｄは決まらない→もし、ｃ・ｄが５６以上５９以下であれば答えがでない。
よって、６０の下は５５。（６０＋５５）÷２＝５７．５

詳しく検証します(´ㅂ`;)
c＜d、４０≦ｃ＜５０、５０≦ｄ＜６０とおく。
平均との差を考えると、＋１４＋１１－１７＋３６－２８－３＋７＋２＝＋２２
ｃとｄで平均との差の合計を－２２にしなければならない。
仮にｃが最も小さい４０と仮定すると、５８－４０＝１８　→平均との差は－１８
ｄの平均との差は２２－１８＝４となり、ｄ＝５８－４＝５４となる。
つまり、ｃを最も小さい値にし、ｄを最も大きい値にしても、
５６≦ｄ≦５９にはならないので、６０の下は５５になる。

大問８（立体図形）

（１）１２√２ｃｍ³
*底面積は正三角形。高さは３。
２√３×３×１/２×４√６×１/３＝４√１８＝１２√２ｃｍ³

（２）１３：２５
*難問。高校数学で習う、ある定理を知らないと厳しい。
△ＡＤＦも△ＯＦＥも断面ＡＭＯ上にあるので△ＡＭＯを考える。
ＡＭは３。Ｄは△ＡＢＣの重心である。
正三角形の各頂点から同じ長さ１０ｃｍを上に伸ばしＯで交点、
Ｏから底面ＡＭに垂直な線をおろすと、底面との交点が正三角形ＡＢＣの重心にあたる。
ＡＤ：ＤＭ＝２：１。よって、ＡＤ＝２ｃｍ、ＤＭ＝１ｃｍ。
（これがわからなくても、△ＯＡＤ内で三平方を使えば求められるはず）

他の辺の比も求めたい。そこで使うのが角の二等分線。

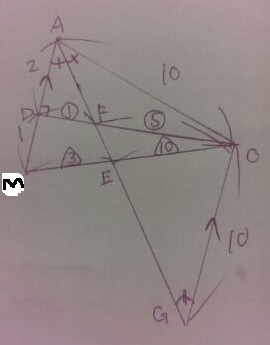
ＡＭに平行でＯを通る線と、ＡＥの延長線との交点をＧとおく。
△ＡＤＦ∽△ＧＯＦとなり、ＤＦ：ＦＯ＝２：１０＝１：５
また、△ＡＭＥ∽△ＧＯＥとなり、ＭＥ：ＥＯ＝３：１０

これで必要な情報がそろった。

おすすめはＭＦに補助線をひく。
△ＡＤＦを２×１＝２とおく。△ＡＤＦ：△ＭＤＦ＝２：１、△ＭＤＦ＝１。
△ＭＤＦ：△ＭＦＯ＝ＤＭ：ＦＯ＝１：５、△ＭＦＯ＝５。
△ＦＭＥ：△ＦＥＯ＝ＭＥ：ＥＯ＝３：１０、△ＦＥＯ＝５×10/13＝５０/１３
よって、△ＡＤＦ：△ＯＦＥ＝２：５０/１３＝２６：５０＝１３：２５

覚えておこう↓

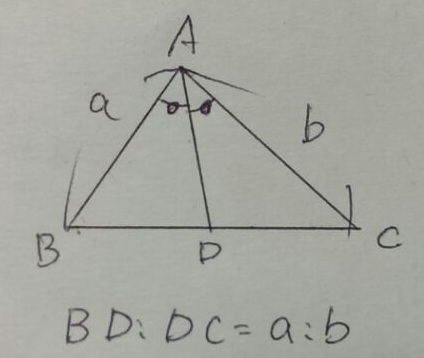
頂角の２等分線は、底辺をこのように内分します。
高校１年生で習います。証明方法は先の解法通り、平行線を作図して相似。
公立高校入試解説ページに戻る