2014年度　千葉県公立高校入試【前期】数学解説

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）８－（－１３）
＝８＋１３＝２１

（２）（－３）²＋（－１/３）×６
＝９－２＝７

（３）（７ａ－４ｂ）＋１/２（２ｂ－６ａ）
＝７ａ－４ｂ＋ｂ－３ａ
＝４ａ－３ｂ

（４）0.2ｘ（ｘ－２）＝ｘ＋1.2
２ｘ（ｘ－２）＝１０ｘ＋１２　←全てを１０倍
２ｘ－４＝１０ｘ＋１２
－８ｘ＝１６
ｘ＝－２

（５）√４８－√２７＋５√３
＝４√３－３√３＋５√３　←全部ルート３にする
＝６√３

（６）二次方程式ｘ²＋７ｘ＋５＝０　を解きなさい。
因数分解できないので、解の公式 を用いる。
ｘ＝（－７±√２９）/２

大問２（小問集合）

（１）
連続する正の整数を適当にもってきて調べてみる。
（３と４、１２と１３、５５と５６・・・など）
すると、エのみが偶数となる。
*偶数と奇数の和、差、積の関係性は覚えておこう。
とくに、積が奇数となる場合は、全てが奇数の項のみ。

（２）
ｙ＝ａｘ²とおいて、ｘとｙに値を代入。
１＝２²ａ
４ａ＝１
ａ＝１/４
よって、ｙ＝１/４x²

（３）
めずらしく標本調査からの出題。
取り出した５０個のうち、オレンジ：白＝４：４６＝２：２３
母集団もこの割合は変わらないと推測。
オレンジは２００個入れたので、白球は２００×２３/２=２３００個

（４）
確率・・・（起こりえる場合）/（全体の場合の数）
全体の場合の数・・・６枚から２枚選ぶ。₆Ｃ₂ ＝(６×５)/(１×２)＝１５通り
起こりえる場合・・・（２，３）（２，４）（２，６）（２、８）（３，６）（３．９）（４．８）の７通り
よって、７/１５

（５）
恒例の作図問題。
作図の前にどうすれば面積が半分の円の半径を描けるかを考える必要あり。
やや難。

仮に、 小さい円の半径をｒと置く。
小さい円の面積はπｒ²
円Ｏの面積は２倍なので、２πｒ²

（円Ｏの半径）×（円Ｏの半径）×π＝２πｒ²　 ←両辺からπを取り除く
（円Ｏの半径）²＝２ｒ²
円Ｏの半径＝√２ｒ
つまり、 円Ｏの半径：小さい円の半径＝√２ｒ：ｒ＝√２：１

√２や１がでてくる図形といえば、直角二等辺三角形。
つまり、円Ｏの半径を斜辺とする直角二等辺三角形を描き、
斜辺以外の１辺の長さが小さい円の半径の長さとなる。

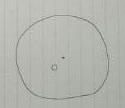
初期状態。（丸がうまく書けない・・）

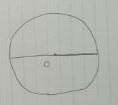
円Ｏの中心を通るように、適当な直径をひく。

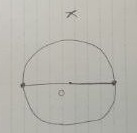
両端からコンパスで、ちょこ、ちょこ。

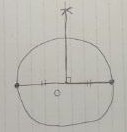
垂直二等分線。

その交点をＡとし、直径の右端をＢとおく。
ＡＢに線を引く。ＡＢは直角二等辺三角形。∠ＡＢＯは４５°。

ＡとＢからコンパスで、ちょこちょこ。

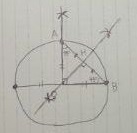
ＡＢの垂直二等分線。ＡＢとの交点をＨとおく。
△ＯＨＢは、９０°、４５°、４５°なので直角二等辺三角形。

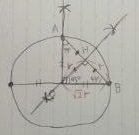
△ＯＨＢが直角二等辺三角形なので、１：１：√２が使える。
ＯＢを２√ｒといくと、ＯＨがｒになる。
つまり、OHが小さい円の半径。

ＯＨを半径にグルッと一周。
青い円が答え。

大問３（グラフ上の図形）

（１）

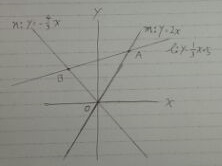
点Ａは直線ℓとｍの交点。
よって、２ｘ＝１/３ｘ＋５
６ｘ＝ｘ＋１５
５ｘ＝１５
ｘ＝３　→Ａのｘ座標は３
直線ｍ：ｙ＝２ｘに代入。ｙ＝２×３＝６
よって、Ａ（３、６）

（２）
Ｂの座標も同様に求める。
－４/３ｘ＝－１/３x＋５
－４ｘ＝－ｘ＋１５
－５ｘ＝１５
ｘ＝－３　…Ｂのｘ座標
ｙ＝－４/３ｘに代入。
ｙ＝－４/３×－３＝４
よって、Ｂ（－３、４）

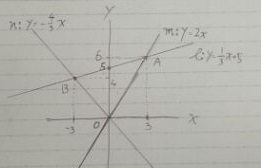
直線ℓの切片は５。
あとは、おなじみの等積変形で、点Ａ、Ｂをｘ座標へ平行移動。

従って、△ＯＡＢの面積は、６×５÷２＝１５ｃｍ²

（３）
やや難。関数の問題で、なぜか図形の回転移動があらわれてキョどる。
長さのわかるところから地道にひも解いていく。

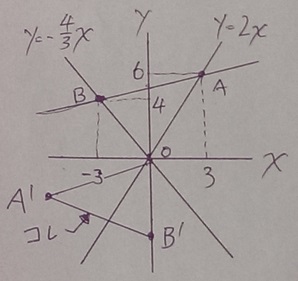
ＯＢがｙ軸に接するとこんな感じ。反時計回しして左にビヨンと三角形が伸びる。
移動後の点Ｂを点Ｂ’とする。
Ａ’とＢ’は第３象限（左下）にくるので、ｘ、ｙ座標ともに負の数になるはず。

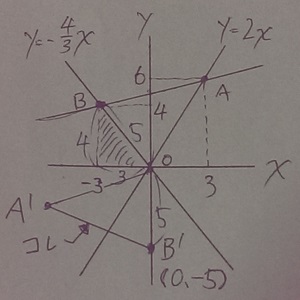
ここで青く塗られた三角形に注目！
傾きが－４/３ということは、４下がって３右にいく。
つまり、Ｂからｘ軸に向かって垂線をひいたときにできるこの三角形は、
３：４：５によりＯＢの長さが５ｃｍということがわかる。
回転移動なので、ＯＢ’も５ｃｍ。Ｂ’の座標は（０、－５）となる。

次に赤に塗られた三角形に注目。
同じようにして、三平方の定理を頼りにＯＡを求める。
ＯＡ²＝６²＋３²＝４５
ＯＡ＝３√５
ＯＡ’も３√５

また、（２）より△ＯＡＢの面積が１５ｃｍ²ということがわかっている。
そこで、ＯＢ’を底辺としたときの高さを求める。

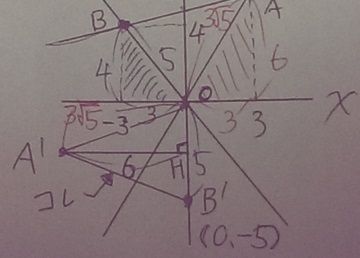
Ａ’からｙ軸に向かって垂線をひき、その交点をＨとおく。
ＯＢ’＝５であるから、Ａ’Ｈ＝１５×２÷５＝６
よって、Ａ’のｘ座標は－６とわかる。

さらに、△ＯＨＡ’（横に長い三角形）内で三平方の定理を用いる。
ＯＨ²＝（３√５）²－６²＝４５－３６＝９
ＯＨ＝３
よって、Ａのｙ座標は－３。
Ａ（－６、－３）

*関数の図形は等積変形による平行移動が主流だが回転移動がでてくるとは。
何度回ったのか、中学数学では計算できないので素直に三平方で頑張る。

大問４（平面図形）

（１）
（a）△ABEと△BCDにおいて、辺BEに対応する辺を選べばよい。
答えはウのCD。

（ｂ）
【１】～【３】をみて明らか。オの二辺の比と夾角が等しい。

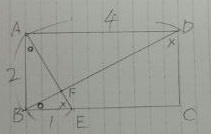
ABCDは長方形なので、ABとDCが平行。
錯角により、∠BDC＝∠DBA

すると、△ＡＢＦと△ＢＥＦにおいて、二角が等しくなるから、
△ＡＢＦ∽△ＢＥＦ

以下、模範解答。
～～引用はじめ～～
【４】より、　∠BAE＝∠CBD　　・・・【５】
∠AEB＝∠BDC　　・・・【６】
△ＡBFと△ＢEFにおいて、
∠BAF＝∠EBF　　　・・・【７】
AB//DCで、平行線の錯角は等しいので、
∠ABF＝∠BDC　　・・・【８】
【６】、【８】より∠ABF＝∠BEF　　・・・【９】
【７】、【９】より２組の角が、それぞれ等しいので、
△ＡBF∽△ＢEF
～～引用おわり～～
*図形が複雑ではないうえ、証明問題としては記述もしやすかった。

（２）
難。
初期状態。

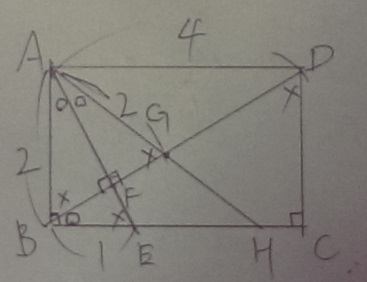
前問の相似を利用して、等しい角度に○や×をつける（○＋×＝９０）。
△ＡＢＧはＡＢ＝ＡＧの二等辺三角形。∠AGB＝×
△ＡＧＦ内で∠ＧＡＦ＝○、∠ＡＦＧ＝９０°
ＡＦは二等辺三角形の頂角∠ＢＡＧの二等分線なので、底辺ＢＧを垂直に２等分する。
よって、ＢＦ＝ＦＧ

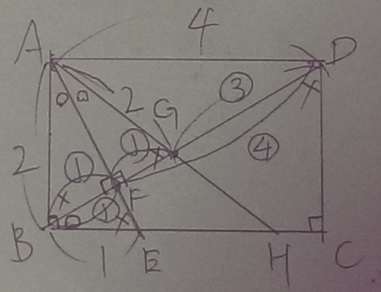
一方で、△ＡＤＦと△ＥＢＦは２角が等しく相似。
ＡＤ：ＥＢ＝４：１だから、ＤＦ：ＦＢ＝４：１
上の写真は比の値を○に入れてみました。
すると・・△ＡＤＧと△ＨＢＧも２角が等しいので相似。
ＧＤ：ＧＢは↑の写真から３：２
よって、ＢＨ＝４×２/３＝８/３ｃｍ

*ＢＨという中途半端なところを求めるので、
ＢＨを１辺とする△ＢＨＧと相似である三角形を探してみよう。
長方形の対角線ＢＤ上の比である、ＢＦ：ＦＧ：ＧＤ＝１：１：３を求めたい。
そのためＡＢ＝ＡＧ→二等辺三角形の性質である、
頂角の二等分線は底辺を垂直に二等分することを利用。

大問５（規則）

（１）
規則性。
行の欄に書かれた数をみると、１，２，３，３，３，２，１，１・・・の規則が続く。
行は８つの固まりで１ループ。つまり、行の数は８の倍数＋余りで決まる。
よって、【ア・・８】

図２を見ての通り、１ループ最後の数である８は４列目にある。
つまり、列は、行のループ数×４＋余りで決まる。【イ・・４】

□　　  □　□　  □　　  □　□　　□ 　　  □　□
□　　  □　　　  □　 　  □　　 　 □　　   □　　… ←２次元で規則の形をおさえておく！
□　□　□　　　 □　□　□　　　  □　□　□　余りがでたとき、どの□に入るのかを見極める
１ループ 　　　２ループ　　　　　３ループ

「１９」のマス目の位置を考える。
行は１ループ８個の規則で、列は行のループ数で決まる。行→列の順番で解く。

行は１ループ８個なので、１９＝８×２＋３　この時点で【ウ・・２、エ・・３】
「１９」は２ループ＋３、すなわち、３ループ目の３番目にくる。よって３行目。

列では、４×２ループ＋１ ＝９列目
最後の＋１は、１ループの最初の３つ目までは同じ列にくるため。

□　　  □　□　  □　　  □　□　　□ 　　  □　□
□　　  □　　　  □　 　  □　　 　 □　　   □　　…
□　□　□　　　 □　□　□　　　  19　□　□
（*２０は＋２、２１は＋３、２２も＋３、２３も＋３、２４は＋４）
よって、【オ・・３、カ・・９】

「２０１４」のマス目の位置も同様。
２０１４÷８＝２５１・・６
つまり、「２０１４」は２５１ループ＋６番目。
６番目なので２行目。
列は、２５１×４＋３＝１００４＋３＝１００７
【キ・・２、ク・・１００７】

（２）
緻密な調査が求められる。
頭がヘロヘロな状態だと、いい加減な計算になりがちでミスしやすい。
使うのは主に相似。

「３３」がどのマス目にくるかを考える。
３３÷８＝４・・１
従って、「３３」は５ループ目の一番左上にくる。
３３～４７まで図示してみる。

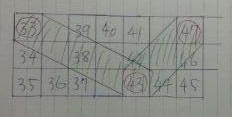
上から下にさがり、V字でまたあがる。
斜線の部分の面積を求める。
３３～４３、４３～４７と左右に分けて考える。

まずは左から。

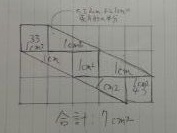
横２個分の長方形の半分は１ｃｍ²
このようにくぎれば、７ｃｍ²とわかる。

同様に右。

正方形の半分同士合わせて１ｃｍ²
合わせて５ｃｍ²

しかし、ダブリの部分がでてしまっている。

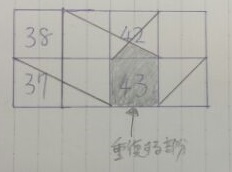
ここを引かなければ正解にたどり着けない。
「４３」のマスは１ｃｍ²とわかるが、「４２」の下部に小さな屋根がある。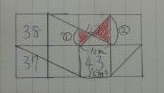
４２に注目。
左右の三角形は二角が等しいので互いに相似。
正方形の１辺を【２】とおく。右の三角形の辺の長さは【２】。
左の三角形は、横２マスの長方形の対角線の真ん中なので中点を通り【１】となる。
左右の三角形の辺の比は２：１。

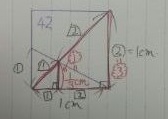
さらに「４２」をピックアップ。
屋根の高さを求めたい。三角形と線分の比を駆使。
大きい三角形と小さい三角形の比は３：１
屋根の高さは１×１/３＝１/３cm
屋根の面積は１×１/３÷２＝１/６ｃｍ²
ダブリの部分は「４３」のマス目と合わせて、１＋１/６=７/６cm²
よって、答えは７＋５－７/６＝６５/６ｃｍ²
公立高校入試解説ページに戻る