平均46.0点(前年比;-0.1点)
問題はこちら→リセマムさん
大問1(小問集合)
(1)
3×(-5)
=-15
(2)
2(3a-2b)-3(a-2b)
=6a-4b-3a+6b
=3a+2b
(3)
x2-3x-4
=(x+1)(x-4)=0
x=-1、4
(4)
ネジレ→延長しても交わらない、かつ平行でもない。
辺CG、辺DH、辺EH、辺FG
(5)
x-y=-x+4y=3
x-y=3…①
-x+4y=3…②
これを解いて、x=5、y=2
(6)
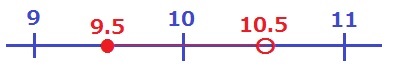
四捨五入で整数→小数第1位の5に注目。
不等号に気をつけよう!10.5を四捨五入で整数に丸めると11になる。
9.5≦a<10.5
(7)
x2+2xy+y2
=(x+y)2 ←ここで代入
=(√2+1+√2-1)2
=(2√2)2=8
(8)
何をx、yに置いたのか注意しよう!
xは往復の時間、yはふりこの長さ。
yに長さを代入する。
■y=1のとき
1=1/4x2
x2=4
x>0より、x=2
■y=9のとき
9=1/4x2
x2=36
x>0より、x=6
往復時間は1mの振り子が2秒、9mの振り子が6秒。
6÷2=3往復
*ふりこの周期はおもりの重さや振れ幅ではなく、
ふりこの長さに依存する。これを振り子の等時性という。
(9)
2x-y=5
yで場合分け。
◆y=1
2x=6、x=3
◆y=3
2x=8、x=4
◆y=5
2x=10、x=5
*2xは偶数、5は奇数なので、等式が成り立つにはyが奇数でなければならない。
→y=1、3、5
計3通り
全体は6×6=36通りだから、確率は3/36=1/12
(10)
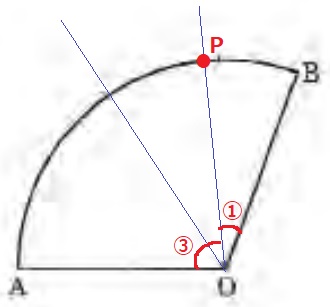
弧の長さは中心角の大きさに比例する。
弧AP:弧PB=3:1とするには、その中心角を3:1にすればいい。
∠AOBを二等分、さらに二等分したB側がPとなる。
大問2(規則)
(1)

なかの白は正方形。
5番目の白の数は、5×5=25個
ア…25
5番目の全体の正方形は1辺が7個。
全体から白をひいて黒の数が求まる。
7×7-25=24
イ…24
全体の正方形の1辺は、
1番目→3個、2番目→4個、3番目→5個…
n番目はn+2個。
タイルの総数は(n+2)2個。
白の1辺n個だから、白の数はn2個。
黒の数は、(n+2)2-n2=4n+4
@別解@
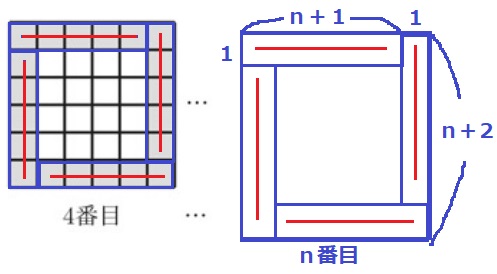
魔方陣でよくある手口。
黒の数は、(n+1)×4=4n+4個
(2)
白…n2個、黒…4n+4個
n2-4n-4=92
n2-4n-96
=(n-12)(n+8)=0
n>0より、n=12
12番目
大問3(小問集合)
(1)
問題文から文字式をつくれるか。
料金の合計は2000a+1200b+500×40円
これを40で割ればいい。
(2000a+1200b+500×40)÷40
=50a+30b+500円
(2)
1人の面積は等辺が5/2mの二等辺三角形。
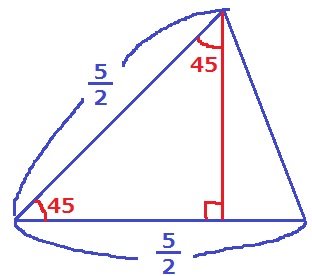
二等辺の頂角は、360÷8=45°
うえのように垂線をひくと内角が45°-45°-90°の直角二等辺が見つかる。
辺の比は1:1:√2で斜辺が5/2mだから、
高さは5/2×1/√2=5√2/4m
面積は、5/2×5√2/4÷2=25√2/16m2
(3)
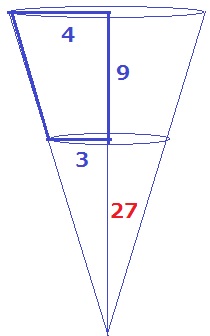
下に延長して円錐を作成。
直角三角形の相似から、下の円錐の高さは27cm。
4×4×π×36÷3-3×3×π×27÷3
=192π-81π=111πcm3
大問4(関数)
(1)
y=3/xにx=-1を代入して、y=-3
(2)
y=-3x2に代入。
x=-2のとき、最小値y=-12
x=0のとき、最大値y=0
-12≦y≦0
(3)
(1)よりA(-1、-3)
Bは原点に関してAに対称なので、B(1、3)
PはOBの中点だから、P(1÷2、3÷2)=P(1/2、3/2)
C(0、4)→P(1/2、3/2)
右に1/2、下に4-3/2=5/2移動する。
→2倍すると右に1、下に5移動する→傾きは-5
切片はCのy座標だから、y=-5x+4
(4)

関数で角度の活用が出題された。
∠OCP=①とすると∠BPC=②

Pを通るy軸に平行な線をひく。
錯角で∠BPCの左側が①
右側は①になり、同位角で∠COP=①
△OCPは底角が①で等しく、二等辺三角形になる!
Pからy軸に向けて垂線。その交点はOCの中点でy=2
Pのy座標が2。これをy=3xに代入。
P(2/3、2)
@別解@

y軸との平行線は∠BPCの二等分線であり、
これを対称の軸とすると、Pを通る2本の直線は線対称の関係。
傾きは3⇒-3。切片は4だから、y=-3x+4
Pはy=3xとy=-3x+4の交点となり、
3x=-3x+4
x=2/3
これをy=3xに代入してP(2/3、2)
大問5(平面図形)
(1)(a)
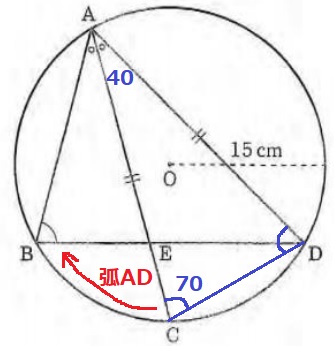
CDに補助線。
仮定より、∠CAD=80÷2=40°
△ACDは二等辺ゆえ、∠ACD=(180-40)÷2=70°
弧ADに対する円周角で、∠ABD=70°
(b)
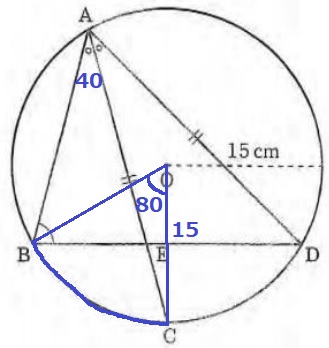
半径はわかっているので中心角さえわかればいい。
∠BACの中心角BOC=40×2=80°
15×15×π×80/360=50πcm2
(2)
△ABC≡△AEDの証明。
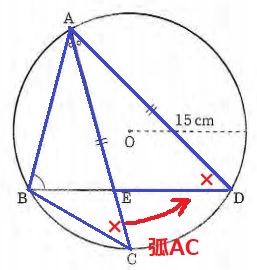
仮定から∠BAC=∠EAD
同じく仮定から、AC=AD
弧ABに対する円周角で、∠ACB=∠ADE
1辺と両端角相等で合同。
(3)
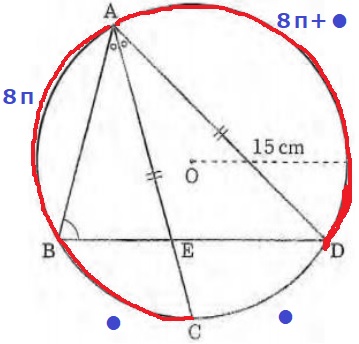
円周角が等しい=弧の長さが等しい。
下の弧BC=弧CD=●とする。
弦AC=弦ADから、赤線の弧の部分が等しい。
弧AC=弧AD=8π+●
円周は15×2×π=30cm
8π+●+●+(8π+●)=30
●×3=14π
●=14/3πcm
弧AD=8π+14/3=38/3πcm
●講評●
大問1
(6)概数は中学受験でもっと難しいのが出る!解けるようにしておきたい。
(8)xではなくyに代入する。
大問2
そんなに難しくはない。計算も複雑ではなかった。
大問3
数学の活用。要点をうまくつかもう。
大問4
(3)までは確実にとりたい。
(4)∠OCPと∠BPCの位置関係から平行線を描きたい。
大問5
(3)円周に着目した設問であった。
どこの弧が等しくなるか、印をつけよう。



コメント