2022年度　栃木県公立高校入試問題過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）　98.8％
14÷（－７）
＝－２

（２）　91.2％
２/３ａ＋１/４ａ
＝11/12ａ

（３）　95.8％
（ｘ＋５）（ｘ＋４）
＝ｘ²＋９ｘ＋20

（４）　79.5％
２ｘ²－３ｘ－１＝０
解の公式を適用して、
ｘ＝（３±√17）/４

（５）　88.9％
ｘ＝３のとき、ｙ＝４
ｘ＝６のとき、ｙ＝２
２≦ｙ≦４

（６）　73.0％
９×２×π×60/360＝３πｃｍ

（７）　77.4％

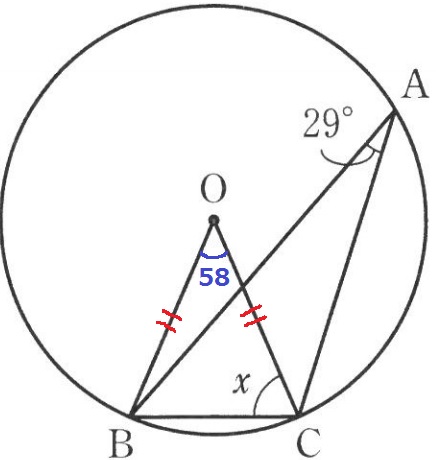
中心角は円周角の２倍なので、∠ＢＯＣ＝29×２＝58°
半径で△ＯＢＣは二等辺だから、ｘ＝（180－58）÷２＝61°

（８）　75.7％
ア：３辺が等しい。
イ：２辺とあいだの角が等しい。
エ：１辺と両端角が等しい。

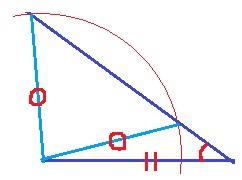
あいだの角でないと、上のように２通りできる。
ウ

大問２（小問集合２）

（１）　53.8％（部分正答含む77.6％）
根号の中が平方数になれば、根号が外れて正の整数になる。
10－ｎ⇒10未満の平方数は１・４・９しかない。
ｎ＝10－１＝９
ｎ＝10－４＝６
ｎ＝10－９＝１
ｎ＝１、６、９

（２）　54.9％（部分正答含む93.2％）
答案では途中の計算も書く。
大人１人がｘ円、子ども１人がｙ円。
２割引き→0.8をかける。

２ｘ＋５ｙ＝3800　…①
0.8（５ｘ＋10ｙ）＝6800　…②

②を整理すると、ｘ＋２ｙ＝1700　…③
①－③×２より、ｙ＝400
③に代入して、ｘ＝900
ｘ＝900、ｙ＝400
大人…900円、子ども…400円

（３）　73.9％（部分正答含む84.7％）
ｘ＝３を代入。
３²－８×３＋２ａ＋１＝０
２ａ＝14
ａ＝７

これを元の式に代入。
ｘ²－８ｘ＋２×７＋１
＝ｘ²－８ｘ＋15
＝（ｘ－３）（ｘ－５）＝０
もう１つの解はｘ＝５
ａ＝７、ｘ＝５

大問３（小問集合３）

（１）　81.7％
全体は６×６＝36通り
積が25以上の場合は（５、５）（５、６）（６、５）（６、６）の４通り。
確率は、４/36＝１/９

（２）　91.2％
赤色のキャップは50個中15個の割合とみなす。
800×15/50＝240個

（３）①四分位数…62.0％（部分正答含む84.5％）、箱ひげ図…59.0％
データを昇順に並べると、
【１・３・４・５・６・６・８・11・13・13・15・21】
12個の第２四分位数（中央値）は６番目と７番目の平均で７日。
第１四分位数は下位グループ【１・３・４・５・６・６】の真ん中、
すなわち、３番目と４番目の平均で4.5日。
第１四分位数…4.5日、第２四分位数…７日

最小値は１日、最大値は21日。
第３四分位数（Q3）は上位６つの３番目と４番目の平均で13日。

②Ｃ市、範囲と四分位範囲がＢ市よりＣ市の方が大きいから。　72.0％（部分正答含む89.9％）
*範囲（レンジ）＝最大値－最小値
範囲が広い方がデータは散らばる。
四分位範囲＝第３四分位数－第１四分位数
箱の長さで、極端な値を廃した四分位範囲が大きいほどデータは散らばる。

大問４（平面図形）

（１）　76.5％

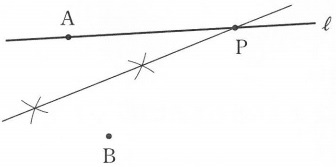
ＡＰ＝ＢＰ→ＰはＡとＢから等距離にある。
ＡＢの垂直二等分線と直線ℓとの交点がＰとなる。

（２）①　73.1％！

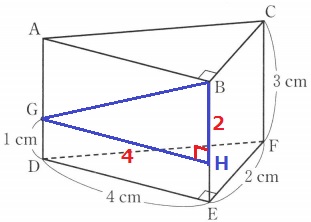
ＢＧを斜辺とする直角三角形ＢＧＨをつくる。
ＢＧ＝√（４²＋２²）＝２√５ｃｍ

②　31.2％！

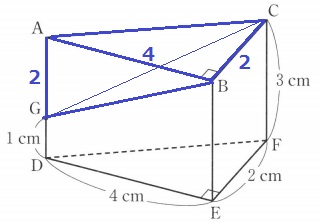
全体の三角柱から上の三角錐を引けばいい。
４×２÷２×３－４×２÷２×２÷３
＝12－８/３
＝28/３ｃｍ³

＠余談＠

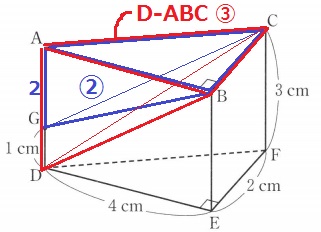
体積比でいけなくもないです。
高さの比であるＡＧ：ＡＤ＝２：３から、
三角錘Ｇ―ＡＢＣの体積を②とすると、三角錘Ｄ―ＡＢＣは③
錘の３倍が柱なので、三角柱ＡＢＣ―ＤＥＦは③×３＝⑨
求積すべき立体の体積は、⑨－②＝⑦
三角柱の７/９倍で求まります。

（３）　45.5％（部分正答含む84.5％）
△ＤＢＣ∽△ＤＣＡの証明。

二等辺ＡＢＣの底角と仮定、共通角をあわせて２角相等→∽

大問５（数量変化）

（１）①　80.7％
ｘ軸について対称移動させると、下に凸が上に凸のグラフに変わる。
ｙ＝－ｘ²

②　56.6％

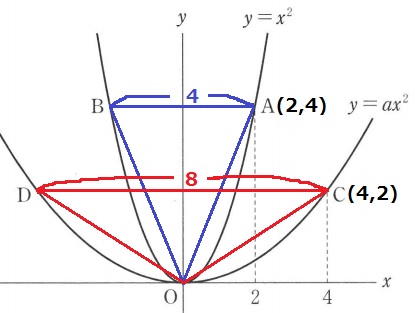
ＡＢ＝４、ＣＤ＝８
△ＯＡＢと△ＯＣＤの面積は等しい→底辺２倍なら高さ半分。
△ＯＡＢの高さはＡのｙ座標である４。
△ＯＣＤの高さにあたるＣのｙ座標は４÷２＝２
Ｃ（４、２）をｙ＝ａｘ²に代入。
２＝16ａ
ａ＝１/８

③　12.2％！（部分正答含む26.1％）
答案では途中の式も書く。

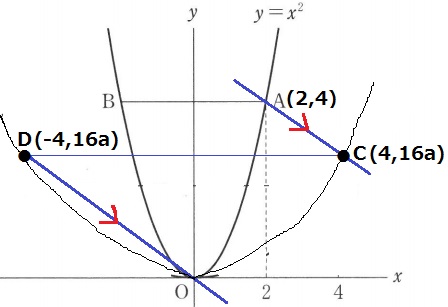
傾きが平行→傾きが等しい点から等式を立てる。
Ａ（２、４）⇒Ｃ（４、16ａ）
ＡＣの傾きは、（16ａ－４）/（４－２）＝８ａ－２
Ｄ（－４、16ａ）⇒Ｏ（０、０）
ＤＯの傾きは、（０－16ａ）/｛（０－（－４）｝＝－４ａ

８ａ－２＝－４ａ
ａ＝１/６

（２）①　53.4％
グラフよりＢ社の200ｋＷｈでは7000円なので、
超過分は9400－7000＝2400円
超過分の電気使用量は、2400÷24＝100ｋＷｈ
全体の電気使用量は、200＋100＝300ｋＷｈ

②　33.2％！
Ａ社200ｋＷｈ超は１ｋＷｈあたり28円増加→傾きは28
ｙ＝28ｘ＋ｂ

これに、グラフで与えられた（ｘ、ｙ）＝（200、6800）を代入。
6800＝28×200＋ｂ
ｂ＝1200
ｙ＝28ｘ+1200

③　10.5％！（部分正答含む33.5％）
Ｂ社のグラフが通る（200、7000）はＣ社のグラフが通る（200、7500）より下にあり、
Ｂ社のグラフの傾き24はＣ社のグラフの傾き25より小さい。

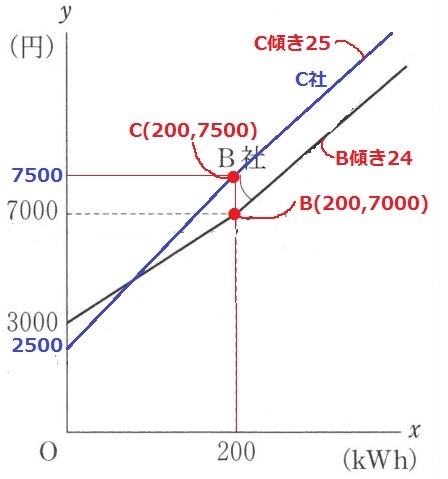
ｘ≧200のＢとＣの比較。
比較すべき数値は出揃っており、言い回しは下線部をまねればいい。
200ｋＷｈではＢ（200、7000）Ｃ（200、7500）でＢの方が安い。
それ以降は傾きに着目する。
Ｂの方が傾きが小さいので両社は交わることなく、徐々に差が広がっていく。
ＣがＢを下回ることはなく、Ｂ社の方が安いと言える。

大問６（規則）

（１）　48.7％（部分正答含む69.0％）
周期をどこに設定するか。
スタートはウだが１回目はエなので、周期のスタートはエ。
右のオに行って中央のウに戻り、左のアに行って中央のウに戻る。
このときが初期状態と同じで、次のエが２ループ目のスタートになる。
周期；【エ⇒オ⇒エ⇒ウ⇒イ⇒ア⇒イ⇒ウ】
19÷８＝２ループ…３
余り３はエ⇒オ⇒エだから、19回目はエとなる。
１ループでエは２回またぎ、余り３で２回またぐから、
２×２＋２＝６度目
エ、６度目

（２）　24.6％！

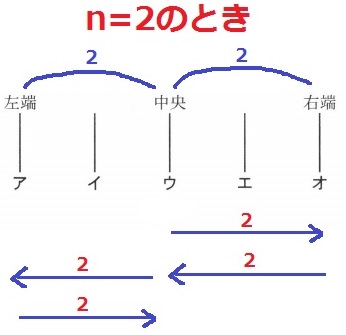
図４のｎ＝２で検証してみると、中央→右端→中央→左端→中央はいずれも２回で、
１往復の全体の回数は、２×４＝８回

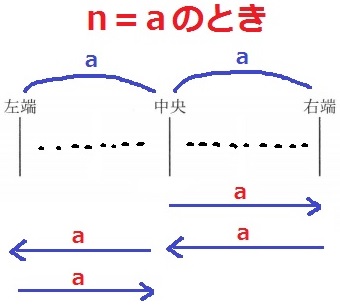
２をａに置き換えても同様。
ｎ＝ａのときの３往復は、４ａ×３＝12ａ回

（３）Ⅰ…11.3％！、Ⅱ…3.5％!!

左から２番目を１度目にまたぐのは、３ｂ回の１個手前。
つまり、３ｂ－１回。

端っこの棒以外は１ループで２回またぐので、
左から２番目の線を12回またいだということは６往復した。
６往復の全体の回数は、４ｂ×６＝24ｂ回

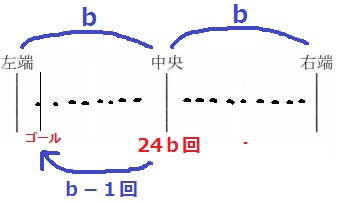
行き過ぎたｂ－１回分戻ればいい。
24ｂ－（ｂ－１）＝23ｂ＋１
これがⅠの（３ｂ－１）の８倍に等しい。

８（３ｂ－１）＝23ｂ＋１
24ｂ－８＝23ｂ＋１
ｂ＝９
Ⅰ…３ｂ－１、Ⅱ…ｂ＝９