2020年度　都立高校入試過去問・分割後期【数学】解説

問題はコチラ→ＰＤＦファイル
2020年度・都立（数学）の解説はコチラ。

大問１（小問集合）

（１）
－３＋８×１/２
＝－３＋４＝１

（２）
７ａ＋９ｂ－（ａ＋４ｂ）
＝７ａ＋９ｂ－ａ－４ｂ
＝６ａ＋５ｂ

（３）
（１－√３）²
＝１－２√３＋３
＝４－２√３

（４）
４ｘ＋９＝６ｘ－５
２ｘ＝14
ｘ＝７

（５）
２ｘ＋３ｙ＝８　…①
４ｘ－５ｙ＝－６　…②
①×２－②
４ｘ＋６ｙ＝16
－)４ｘ－５ｙ＝－６
11ｙ＝22
ｙ＝２
①に代入。
２ｘ＋６＝８
ｘ＝１
ｘ＝１、ｙ＝２

（６）
ｘ²＋ｘ－72
＝（ｘ＋９）（ｘ－８）＝０
ｘ＝－９、８

（７）
ａ＞０なのでグラフは下に凸。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－３のとき、最大値ｙ＝27
０≦ｙ≦27→ウ

（８）
６個から２個を取り出す→₆Ｃ₂＝15通り
同じ色には番号を付けて区別する！
白₁・白₂から１つ、青₁・青₂・青₃から１つ取り出す→２×３＝６通り
確率は６/15＝２/５
あ…２、い…５

（９）
垂線の作図。
①Ｃに針をセットして適当な弧を描く。
②ＡＢとの交点から適当な２つの弧を描く。
③その交点とＣを結び、ＡＢとの交点がＰとなる。

大問２（式の証明）

（１）
表面積Ｐを求める。

底面の正六角形は６分割しよう。
ｃ×ａ÷２×６＋ｃ×ｂ÷２×６
＝３ａｃ＋３ｂｃ
＝３ｃ（ａ＋ｂ）→ア

（２）
証明問題。円錐の表面積Ｑを導く。
底面積…ｒ×ｒ×π＝πｒ²
側面積…扇形の中心角が分からない。

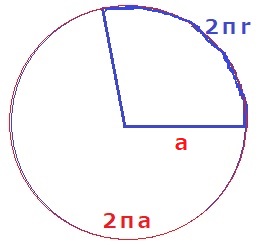
中心角は、全体である円を分母としたときの扇形の割合で代用できるので、
〔円周の長さ÷弧の長さ〕を用いる。
円周は２πａ、弧の長さは底面の円周ℓ＝２πｒ
ａ×ａ×π×２πｒ/２πａ＝πａｒ

表面積Ｑ＝πｒ²＋πａｒ＝πｒ（ａ＋ｒ）
πｒの部分にℓを使う。
ℓ＝２πｒ
πｒ＝１/２ℓ
よって、Ｑ＝１/２ℓ（ａ＋ｒ）となる。

大問３（関数）

（１）
ｙ＝－２ｘ＋８にｘ＝－２を代入。
ｙ＝－２×（－２）＋８＝12
う…１、え…２

（２）①

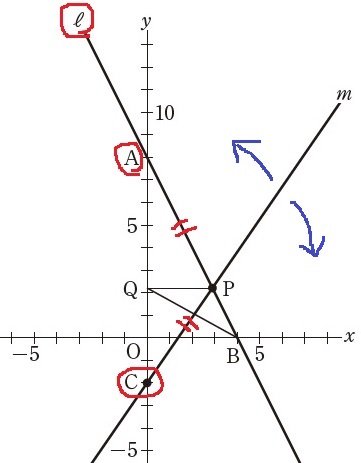
直線ℓ・Ａ・Ｃは固定。
ＡＰ＝ＣＰとなるときのｍの傾きを求める。
なんとなくℓの傾きを負にすればいいような気がする。

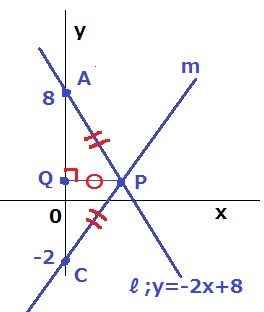
△ＡＰＣは二等辺三角形。
ＱＰはｘ軸に平行で、ＡＣ（ｙ軸）とＱＰは垂直に交わる。
△ＡＰＱと△ＣＰＱは、ＡＰ＝ＣＰ、ＱＰ（共通辺）、垂直から、
斜辺と他の１辺が等しい直角三角形で合同。
言い換えれば、ＱＰを対称の軸として△ＡＰＱと△ＣＰＱは対称関係にある。
ＱＰはｘ軸に平行で、∠ＡＰＱ＝∠ＣＰＱ
ｘ軸からの角度が等しいので、直線ｍの傾きは直線ℓのそれを負にすればいい。
直線ｍの傾きは２→イ

＠別解＠
計算で解く方法もある。
２つの合同な直角二等辺からＱがＡＣの中点とわかれば、Ｑ（０、３）
Ｐのｙ座標は３で、直線ℓに代入するとＰ（５/２、３）
ＰとＣを通る直線の式から、
３＝５/２ａ－２
ａ＝２

②
①とは別問なので、ＡＰ＝ＣＰの設定が外れる。

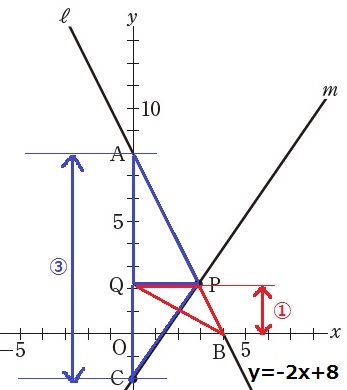
△ＡＣＰを△ＡＰＱ＋△ＣＰＱに分割しよう。
ＰＱを底辺として、高さの合計ＡＣ＝10を③とすると、
△ＢＰＱの高さは①となる。
①＝10×１/３＝10/３
Ｐのｙ座標が10/３で、これをｙ＝－２ｘ＋８に代入。
10/３＝－２ｘ＋８
２ｘ＝14/３
ｘ＝７/３

大問４（平面図形）

（１）

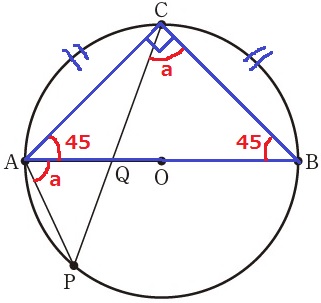
弧ＢＰの円周角より、∠ＢＣＰ＝ａ
１つの円において、弧が等しければ弦の長さも等しい→ＣＡ＝ＣＢ
直径に対する円周角は直角で∠ＡＣＢ＝90°から、△ＡＢＣは直角二等辺三角形。
△ＣＢＱで外角定理→∠ＡＱＣ＝ａ＋45°
エ

（２）①
△ＡＰＣ∽△ＱＡＣの証明。

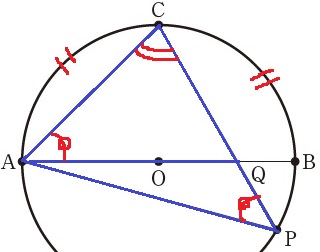
辺の情報が乏しいので角度攻め。
弧が等しければ円周角が等しい→∠ＡＰＣ＝∠ＱＡＣ
共通角∠ＡＣＰ＝ＱＣＡと合わせて２角相等で∽。

②

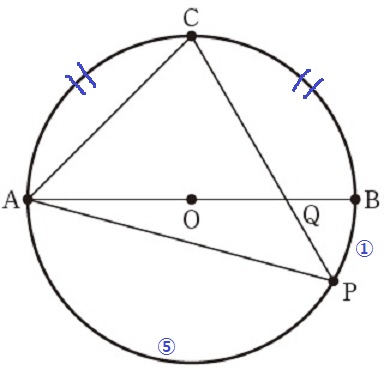
弧の長さしかわかっていない。
求めたいのは△ＡＰＣと△ＱＡＣの面積比。
これを知るには、ＣＰ：ＣＱを知ればいい。

弧の長さからわかる情報は中心角。
中心Ｏから補助線をいれて中心角に着目する。

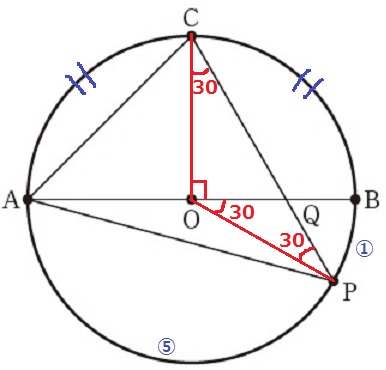
ＯＣとＯＰに補助線。
円周の上半分で、Ｃは弧ＡＢの中点だから、∠ＢＯＣ＝180÷２＝90°
円周の下半分で、弧ＡＰ：弧ＰＢ＝⑤：①より、∠ＢＯＰ＝180°×１/６＝30°
半径より△ＯＣＰは二等辺で、∠ＯＣＰ＝∠ＯＰＣ＝（180－90－30）÷２＝30°

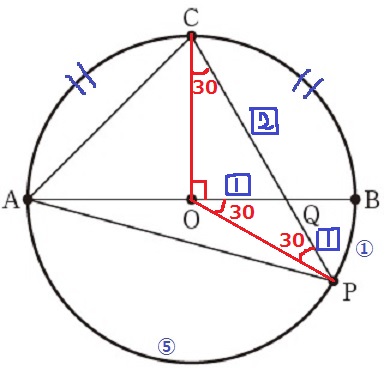
ＯＱの長さを【１】とする。
△ＣＯＱの内角は30°－60°－90°より、１：２：√３からＣＱ＝【２】
△ＯＰＱは二等辺で、ＱＰ＝【１】

ＣＰ：ＣＱ＝３：２より、△ＡＰＣと△ＱＡＣの面積比は３：２
お…３、か…２

大問５（空間図形）

（１）

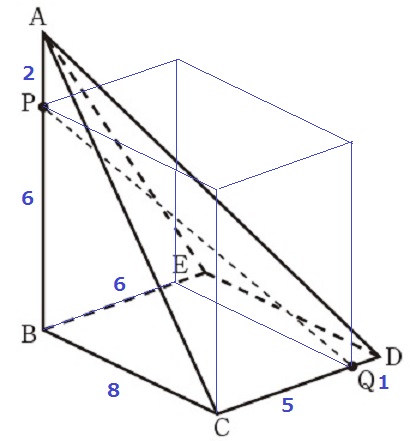
空間をナナメに横切る線分の長さは、それを対角線とする直方体を作図するのが定石。
１辺の長さがａ、ｂ、ｃの直方体の対角線の長さ→√（ａ²＋ｂ²＋ｃ²）

ＰＱ＝√（５²＋８²＋６²）
＝√125＝５√５ｃｍ
き…５、く…５

（２）

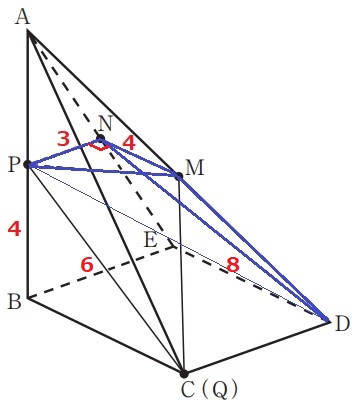
ＰＤに補助線。
Ｍ－ＰＱＤＮを三角錘Ｍ－ＰＤＮと三角錘Ｐ－ＭＣＤに分割してみた。
三角錘Ｍ－ＰＤＮは、底面を△ＰＭＮとすると高さはＢＰ＝４ｃｍ
３×４÷２×４÷３＝８ｃｍ³

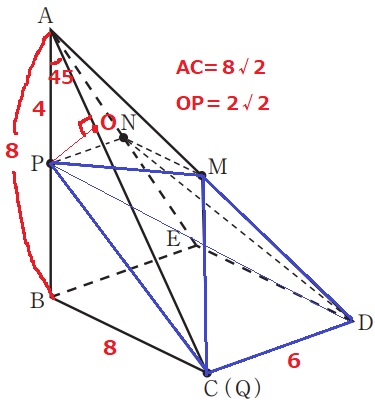
問題は三角錐Ｐ－ＭＣＤの体積。
底面は△ＭＣＤで捉える。

△ＡＢＣは直角二等辺で、１：１：√２よりＡＣ＝８√２ｃｍ
△ＡＣＤの面積は、６×８√２÷２＝24√２ｃｍ²
ＭはＡＤの中点なので、△ＭＣＤ＝24√２÷２＝12√２ｃｍ²

この△ＭＣＤは面ＡＣＤ上にある図形なので、Ｐから辺ＡＣに向けて垂線をおろし、
その足をＯとすると、ＰＯが高さに相当する。
∠ＢＡＣ＝45°から、△ＡＰＯも直角二等辺→ＰＯ＝２√２ｃｍ
よって、三角錐Ｐ－ＭＣＤの体積は、12√２×２√２÷３＝16ｃｍ³

したがって、Ｍ－ＰＱＤＮの体積は、８＋16＝24ｃｍ³
け…２、こ…４

＠2020年度（都立）＠
数学…平均61.1点　社会…平均57.0点　理科…平均53.4点　英語…平均54.7点
その他は下記リンクの目次からどうぞです。
公立高校入試解説ページに戻る