問題ＰＤＦ
表１は、水の温度と物質Ａが水100ｇに溶ける最大の重さの関係を示したものです。
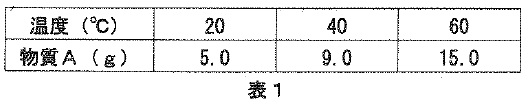
計算問題の答えは、整数または小数で答え、
割り切れない場合は小数第２位を四捨五入して、小数第１位まで答えること。
（１）
20℃における物質Ａの飽和水溶液が100ｇあった場合、何％の濃さになりますか。
（２）
60℃における物質Ａの飽和水溶液100ｇを40℃まで下げた場合、
溶けきれなくなって出てくる物質Ａは何ｇですか。
次に、物質Ａと水に溶けない物質Ｂを均一に混ぜたものをＸｇ用意しました。
物質Ｂの量を求めるために、実験１～４を行いました。
実験１：Ｘｇを三等分し、ビーカー①～③に入れました。
実験２：ビーカー①にある量の水を加え20℃にしたところ、
19.0ｇの固体が溶けずに残りました。
実験３：ビーカー②に実験２と同じ量の水を加え40℃にしたところ、
14.2ｇの固体が溶けずに残りました。
実験４：ビーカー③に実験２と同じ量の水を加え60℃にしたところ、
10.0ｇの固体が溶けずに残りました。
（３）
Ｘｇ中に含まれていた物質Ｂは何ｇですか。
（４）
実験２で加えた水の量は何ｇですか。
＠解説＠
見た目のわりにつっかかりやすい(´ﾟдﾟ｀)
（１）4.8％
５％じゃないよ(‘д‘⊂彡☆))Д´)ﾊﾟｰﾝ
20℃では水100ｇに対し、物質Ａは5.0ｇ溶ける。（水溶液は105ｇ）
水溶液を100ｇにしたとき、物質Ａは５×100/105＝100/21ｇ溶ける。
濃度は、100/21÷100×100＝100/21％＝4.76…％≒4.8％
（２）5.2ｇ
60℃の水100ｇに物質Ａは15ｇ溶ける。（水溶液は115ｇ）
60℃100ｇの飽和水溶液に溶ける物質Ａは、15×100/115＝300/23ｇ
40℃100ｇ飽和水溶液に溶ける物質Ａは、９×100/115＝180/23ｇ
よって、300/23－180/23＝120/23＝5.21…≒5.2ｇ
＠別解＠
はじめは水溶液115ｇと仮定して計算することもできる。
60℃の水100ｇにＡは15ｇ溶ける。（115ｇの水溶液）
40℃の水100ｇで９ｇ溶けるので、６ｇが析出されて出てくる。
ここで、水溶液115ｇ→100ｇに切り替え。
（一定の水溶液に溶ける物質Ａの量の割合は変わらない）
析出量は、６×100/115＝5.21…≒5.2ｇ
（３）30ｇ
①20℃水＋19ｇ
②40℃水＋14.2ｇ
③60℃水＋15ｇ
おのおのの水の量は等しいが、何ｇの水かわかっていない。
ここで水100ｇの表１を確認。
溶解度の差に注目する。
20℃→40℃では４ｇ、40℃→60℃では６ｇの差がある。
20℃→40℃：40℃→60℃＝４：６＝【２】：【３】
この溶解度の差の比は、水の量が変わっても変わらない。
①20℃水＋19ｇ
②40℃水＋14.2ｇ
③60℃水＋10ｇ
①→②…19－14.2＝4.8ｇ
4.8ｇを【２】とすると、【３】は7.2ｇになるが、
②→③では、14.2－10＝4.2ｇしか溶けなかったということは、
③のビーカーは物質Ａがすべて溶けた状態で、固体はＢしかないことになる。
よって、Ｘに含まれていた物質Ｂは10×３＝30ｇ
（４）120ｇ
物質Ｂを除いて物質Ａだけにすると、、
①20℃水＋９ｇ
②40℃水＋4.2ｇ
③60℃水＋０ｇ
本問も溶解度の差に注目する。
①と②におけるＡの差は、９－4.2＝4.8ｇ
表１で、水100ｇのときに20℃→40℃の溶解度の差は４ｇだったので、
実験２で加えた水の量は、100×4.8/４＝120ｇ
難関中学（理科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント