2018年度　早稲田中学２日目過去問【算数】大問５解説

問題ＰＤＦ
図１のように、厚さが一定の壁を平らな地面と垂直に立てたところ、
面積が15ｍ²の長方形の影ができました。
直角三角形の板が壁と平行に、壁から50ｃｍ離れて立ててあります。次の問いに答えなさい。
ただし、直角三角形の板の厚さは考えません。

（１）
図１の壁にうつった影の面積は何ｃｍ²ですか。

（２）
壁を図２のように倒しました。
倒した壁の上面に面積が960ｃｍ²の直角三角形の影ができました。
①壁の厚さは何ｃｍですか。
②直角三角形の板によって光が届かない部分を立体と考えたとき、
その立体の体積は何ｃｍ³ですか。

＠解説＠
（１）
15ｍ³の影から、影の奥行きは15÷３＝５ｍ
２ｍの高さで５ｍの影ができる→【高さ②：影⑤】

壁がなかったとすると、影の先端は、80×５/２＝200ｃｍまで伸びる。
壁～先端は、200－50＝150ｃｍ
壁に映る影の高さは、80×150/200

＝60ｃｍ（もしくは、150×２/５＝60）

直角三角形の底辺も同様。
60×150/200＝45ｃｍ
よって、映った影の面積は、45×60÷２＝1350ｃｍ²

（２）①
ムズイ:( ´ω` ):
算数が得意な子は実力差を見せつけられるか。

ポイントは、壁の厚みに相似図形をくっつける。

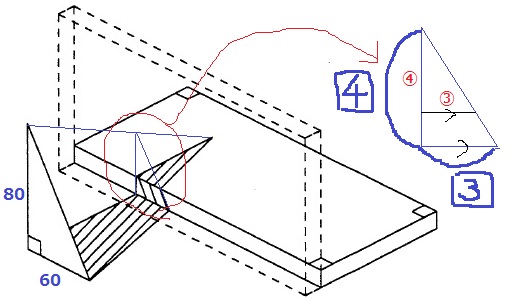
直角三角形の高さ：底辺＝80：60＝４：３
この割合は、直角三角形が厚みに接しても同じ。
さらに、壁の厚みは平行なので、厚みの上の直角三角形も４：３が維持される。

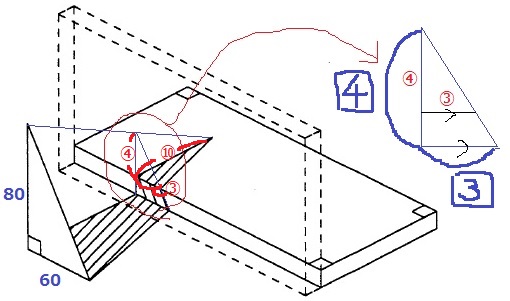
高さ④のとき、影は④×５/２＝⑩
壁の上面の直角三角形は③×⑩÷２＝【15】＝960ｃｍ²
【１】＝64ｃｍ²
面積【１】が64ｃｍ²なので、辺の長さ①は８ｃｍ。（面積＝辺×辺）
④＝８×４＝32ｃｍ

この後も工夫が求められる(;´･ω･)
横から見た様子を作図。

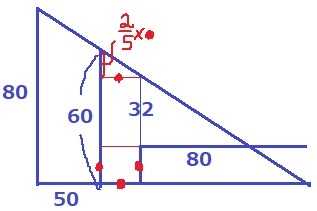
前問の60ｃｍを利用する。
厚みを●として、上のような補助線をひく。
一番上の小さな直角三角形の底辺が●なので、高さは２/５×●となる。
２/５×●＋32＋●＝60
７/５×●＝28
●＝20
壁の厚さは20ｃｍ。

②

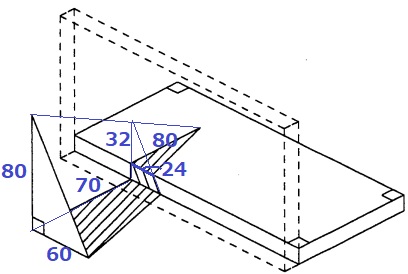
２つの立体に分ける。
手前は、高さ200ｃｍの三角錐の下70ｃｍ分。
80×60×１/２×200×１/３×（20×20×20－13×13×13）/（20×20×20）＋32×24×１/２×80×１/３
＝106060＋10240＝126300ｃｍ³

*板がないと仮定した状態から、板が邪魔して影が作られなかった部分を引いてもできる。
80×60÷２×200÷３－52×39÷２×130÷３×（13³－８³）/13³
＝160000－33700＝126300ｃｍ³
どっちにしろ面倒くさい(´ﾟдﾟ｀)ｙ-00
難関中（算数科）解説ページに戻る