問題ＰＤＦ
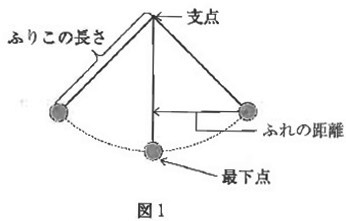
図１のように糸におもりをつけて作った。
このふりこをとりつけた点を「支点」、支点からおもりの中心までの長さを「ふりこの長さ」、
ふりこをふらさずに静止させたときのおもりの位置を「最下点」と呼ぶことにする。
次にこのふりこをふらしたときのことを考える。一番高い位置にあるときのおもりの中心から、
おもりが最下点にあるときの糸への垂直な線の長さを「ふれの距離」と呼ぶことにする。
ふりこの長さを変えて、ふりこの１往復する時間（これを「周期」という）を調べたところ
下表のような結果が得られた。
（１）
ふりこの長さと周期の関係を説明する文としてもっとも適切なものを選びなさい。
ア：ふりこの長さが２倍、３倍になると、周期は４倍、９倍になる。
イ：ふりこの長さが３倍、４倍になると、周期は６倍、８倍になる。
ウ：ふりこの長さが４倍、９倍になると、周期は２倍、３倍になる。
エ：ふりこの長さが５倍、10倍になると、周期は５倍、10倍になる。
オ：ふりこの長さと周期の関係には周期性はない。
（２）
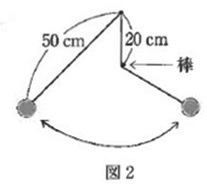
ふりこの長さが50ｃｍのふりこがあります。
このふりこの支点の真下20ｃｍのところに棒を打ち、
図２のような途中で長さが変わるふりこを作りました。
このふりこの周期を答えなさい。
次に図２の棒を取り除き、ふりこの長さを変えてから再度ふりこをふらした。
しばらくすると、おもりは最下点付近でわずかにふれ続けた。
このふれの様子を拡大して観察するために暗い部屋に光源を位置し、
スクリーン上におもりの影を映し出す図３のような装置を作成した。
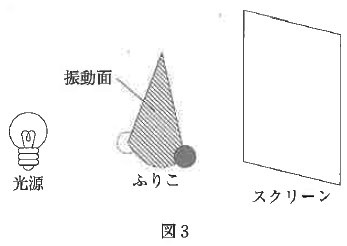
この装置では、ふりこの振動面とスクリーンは平行になっており、
光源の中心と最下点にあるおもりの中心を通る直線はスクリーンに垂直である。
（３）
このときのおもりのふれの距離を求めなさい。
ただし、割り切れない場合は小数第２位を四捨五入し、小数第１位まで答えなさい。
また、おもりとスクリーン上のおもりの影は一直線上で動くものとする。
なお、必要であれば次の直角三角形の関係式を用いること。
今度は一定の速さで回転する回転台に小球を取り付けたものを光源とスクリーンの間に設置し、図４のような装置を作成した。図５は装置を真上から見たもので、スクリーンは地面と垂直に立っており、光源の中心と小球の中心が描く円の中心を通る直線とも垂直になるように置かれている。
スクリーン上に映った小球の影の様子を観察すると、図３の装置で観察したおもりの影のふれの様子とよく似た動きをした。図３、図４それぞれの装置のおもりと小球の影が1.2秒毎に同時にスクリーン右側で折り返すようにふりこの長さと回転台の速さ、回転の開始位置を調整した。
（４）
図４の装置において回転台を回転させたときにスクリーン上に映る小球の影の範囲を解答用紙に描きなさい。ただし、影ができる範囲は解答例のように両矢印で表すこと。また、解答するために用いた線は残しておくこと。
（５）
回転台上の小球の影が動く速さを求めなさい。ただし、小球の中心が描く円の半径が３ｃｍであり、円周率は3.14として計算すること。また、割り切れない場合は小数第２暗いを四捨五入し、小数第１位まで答えなさい。
（６）
おもりと小数の影がスクリーン左側で折り返すタイミングも同時に近づけるための手段として最も適切なものを選びなさい。
ア：回転台上の小球が動く速さを２倍にする。
イ：回転台上の小球が動く速さを半分にする。
ウ：光源の位置を回転台に近づける。
エ：光源の位置を回転台から遠ざける。
オ：回転台の形をだ円にする。
＠解説＠
（１）ウ
ふりこの長さを長くすると周期は長くなる。
オが外れるとして、残りは表から具体的な数値を調べなくてはならない。
〔５ｃｍ－0.45秒〕〔20ｃｍ－0.90秒〕〔45ｃｍ－1.35秒〕
振り子の長さを４倍、９倍すると、周期は２倍、３倍になる。
＠振り子の等時性＠
振り子が左右に１往復する時間を周期という。
周期はおもりの重さや振幅ではなく、振り子の長さ（支点からおもりの重心）に依存する。
振り子の長さが一定であれば周期は一定なり、これを振り子の等時性という。
振り子の長さを４倍、９倍すると、周期は２倍、３倍と長くなる。
（もっというと、振り子の長さを２倍、３倍すると、周期は√２倍、√３倍になる）
（２）1.26秒
振り子が右にいくと支点が棒に移る。
振り子の長さを左半分は50ｃｍ、右半分は30ｃｍで計算する。
1.42÷２＋1.1÷２＝2.52÷２＝1.26秒
（３）0.8ｃｍ
問題文から上から見た図を正確に作図する！
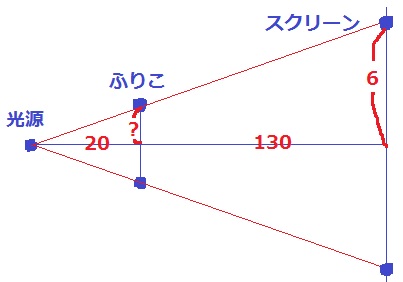
振り子の振動面とスクリーンが平行なので、ここから相似図形を見出す。
振り子の振れの距離は、６×20/150＝0.8ｃｍ
*ちなみに、振幅はおもりが最高点から最下点に移動したときの弧の長さ。
（４）
スクリーンに映る小球の影の範囲を図示する。
回転台がまわると、小球の影が左右に移動する。
どこが影の端にあたるか。
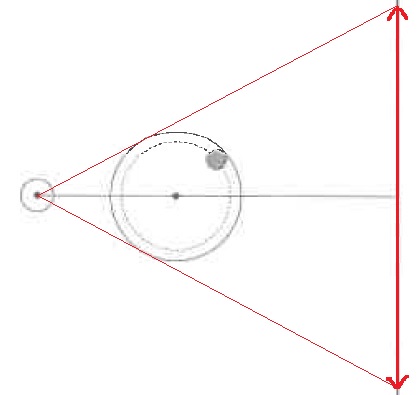
↑答えは赤い矢印。
小球と回転台は１点で交わる。
光源から回転台（小球）に接する接線とスクリーンとの交点が影の端になる。
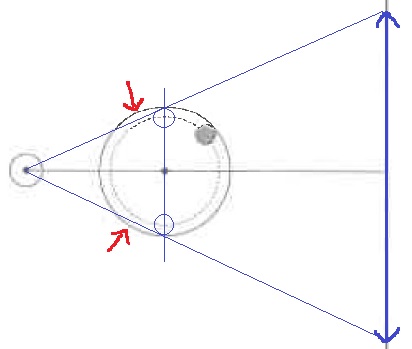
誤答のパターンとしてはこれが多いだろうか。
小球が最も上or下にきたときの小球の端を通る直線だが、
このとき、小球の端は光源から小球に伸ばした接線の内側にあるので、光が当たっていない。
また、この位置の小球に接する接線を引いた影の範囲であっても、
接線が回転台の内部（赤い矢印のところ）に食い込んでしまっており、影はまだ左右に伸びる。
前図のように、小球は回転台の接線と交わる位置にある。
（５）秒速15.7ｃｍ
小球の影が1.2秒毎ごとにスクリーンの右端で折り返すので、周期は1.2秒。
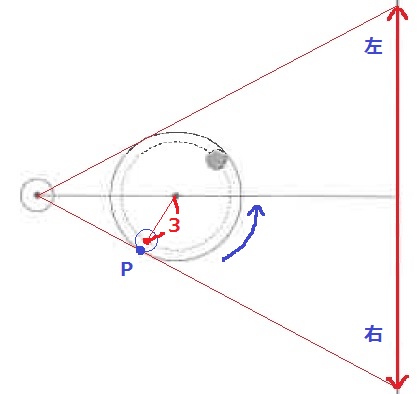
スクリーンの右側に影ができたとき、接線と小球が交わる点をＰとする。
回転台が回転すると、Ｐは回転台の円周上をグルグルまわる。
影が右側で折り返す周期が1.2秒毎なので、Ｐが１周してもとの場所に戻るのも1.2秒毎。
つまり、回転する１周の長さを1.2秒でわれば秒速がでる。
求めたいのは小球の速さなので、小球の中心を基礎として計算する。
３×２×3.14÷1.2＝15.7
（６）エ
厳しめ(´･_･`)
初見で発見するには観察力が試される。
右側で1.2秒毎で影がＵターンするのだから、周期は1.2秒で左右の移動は0.6秒毎。
左側も同じタイミングで折り返すのでは？(´・д・｀)
この沼から出られるか…。
図３の振り子は左右で規則正しく触れる。
ポイントは図４の回転台に乗せられた小球の動き。
（４）の解答を眺めてみよう|д･)
接線上にくる２つの小球をみると…左側の中心角が小さく、右側の中心角が大きい。
ということは、左の弧より右の弧が長くなる！
スクリーン右側の折り返しが1.2秒周期なのは小球が1.2秒で１回転するからだが、
左の折り返しも同じくするには、小球の位置が180度反対側にいなくてはならない。
左右で弧の長さが違うので、右→左は0.6秒より遅く、左→右は0.6秒より早くなり、
合計の１往復は1.2秒となる。
では、左右の弧の長さをできるだけ等しくするにはどうするか？
回転速度を変えてしまうと1.2秒の周期が崩れるので×。
回転台を楕円にしても小球の形はそのままなので、
２つの接点を結んだあいだの角（中心角）は変わらず、弧の長さの大小関係も変わらない。
よって、光源と回転台との距離に絞られる。
２つの小球が180度反対の位置関係に近づくのは、光源が回転台から遠い場合。
光源を回転台から遠ざけると、接線が平行に近づいていき、
回転台の左右において中心角の大きさと弧の長さが左右で近似していく。
弧の長さが近くなれば、周期の半分も0.6秒毎になっていく。
*地学分野で北極星の高度が観測地点の緯度に相当すると習うが、
あれは北極と南極の距離の差以上に北極星が地球よりだいぶ遠くにあるため、
地表に差し込んでくる北極星からの光を平行とみなすことができるから。
光は光源から放射状に広がるが、２本の平行線と考えれば同位角が利用できる。
太陽光の話でもでてきますね(‘ω’)
＠単振動と等速円運動＠
振り子の問題になぜ回転台が登場したのか？
振り子が左右に振れる運動も、回転台に載せた小球がグルグルまわる運動も、
周期的に同じ動きが繰り返される共通点がある。
高校物理では振り子の運動を『単振動』と表現する。
単振動はざっくりいうと同じ動きを繰り返す運動。
（振り子はブラブラと左右に、バネはビヨンビヨンと伸びたり縮んだり）
一方で、回転台に乗せた小球は、円周をグルグルと動く円運動をする。
速さが等しい円運動をとくに等速円運動という。
そして、本問のように等速円運動をスクリーンの影を通じて横からみると、
振り子の単振動と似た動きをする。
青い点が等速円運動。青い点の真横にいる赤い点は直線上を上下に移動する。
さらに、どのくらいの量が変化したのか、時間軸にのせて変化量（変位）を描くと波形になる。
これは三角関数（正弦曲線）の形で、物理学では正弦波とよばれる。
このように単振動と等速円運動は密接な関係にあり、
「単振動は等速円運動の正射影（スクリーンに対し垂直にあてた光による影）である」と表現される。
難関中学（理科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント