問題ＰＤＦ
Ａ、Ｂ、Ｃ、Ｄ、Ｅの５人に国語と算数のテストを行い、その結果を表にしました。
表１は国語、算数それぞれの得点と人数を表したもので、表２は得点の合計と人数を表したものです。
テストの結果については以下のことが分かっています。
・Ａの国語の得点とＢの算数の得点の比は３：２です。
・Ｄの国語の得点はＥの国語の得点より３点高いです。
・Ｄは国語の得点と算数の得点が同じです。
・ＣとＥの算数の得点はそれぞれ76点と78点です。
・合計得点が最も高い人はＡで188点です。
（１）
Ｂの算数の得点は表１の（ア）～（エ）のうちどれにあてはまりますか。
また、選んだ理由を簡単に書きなさい。
（２）
５人を算数の得点の高い順に並べなさい。
（３）
Ｃの国語の得点は何点ですか。
＠解説＠
（１）
答案では理由も記述する。
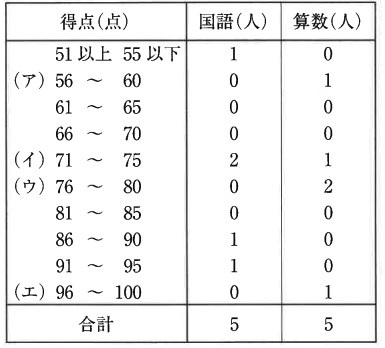
『Ａの国語とＢの算数の比は３：２』に着目する。
もしＢの算数が（イ）だと最低でも71点。
71×３/２をするとＡの国語が100点を超えてしまうので、Ｂの算数は（ア）である。
（２）
算数だけを見る。
前問より、Ｂは56～60点。
Ｄは国語と算数が同点→ともに同じ階級があるのは71～75点。
Ｃ＝76点、Ｅ＝78点だから、Ａは96～100点の階級に含まれる。
得点の高い順にＡ＞Ｅ＞Ｃ＞Ｄ＞Ｂ
（３）
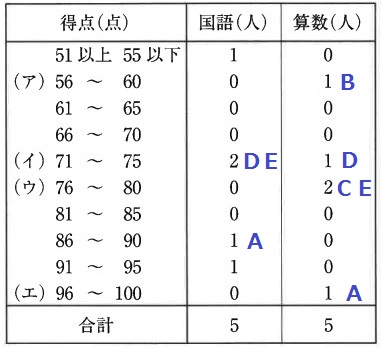
まずは算数を記入する。
Ａの国語：Ｂの算数＝３：２なので、Ａの国語は（56～60）×３/２＝（84～90）
→86～90点の階級がＡ。
Ｄの国語＝Ｅの国語＋３
ＤとＥは同一階級が１つ違いだが、76～80の階級が０人だからＥは71～75の階級。
ＢとＣが決まらない。
そこで合計得点から考える。
Ａの合計得点は188点→181～190点がＡ。
Ｄは国（71～75）＋算（71～75）＝（142～150）→141～150点がＤ。
Ｅは国（71～75）＋算78＝（149～153）→141～150点か151～160点がＥ。
仮にＢの国語を51～55点とすると、Ｂの総合得点は国（51～55）＋算（56～60）＝107～115点
総合得点の階級にないので、Ｂの国語は91～95点、Ｃの国語は残りの51～55点と決まる。
Ｂの合計得点は、国（91～95）＋算（56～60）＝（147～155）→141～150点か151～160点がＢ。
Ｃの合計得点は残りの131～140点の階級。
Ｃの算数は76点だから、Ｃの国語は（131～140）－76＝（55～64）
Ｃの国語の階級は（51～55）に含まれるので、重複する55点。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント