問題ＰＤＦ
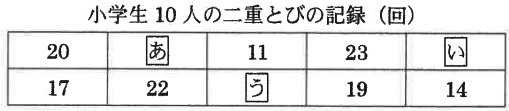
下の表は、小学生10人の二重とびの回数を記録したものです。
この記録の平均値は17.8回、中央値は18.5回でした。
次の問いに答えなさい。
（１）
あ、い、うの３つの値の合計を求めなさい。
（２）
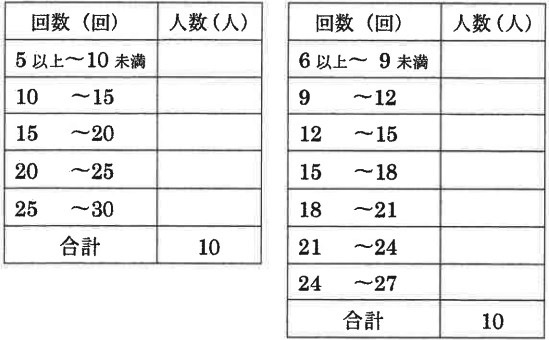
10人の記録を次の２つの表に整理するとき、
どの階級にも少なくとも１人はいることがわかりました。
あ、い、うに当てはまる３つの値を求め、解答欄の左から小さい順に答えなさい。
＠解説＠
（１）
10人の合計は、17.8×10＝178回
判明している７名の合計は、20＋11＋23＋17＋22＋19＋14＝126回
不明の３人の合計は、178－126＝52回
（２）
10人の中央値である18.5回は５番目と６番目の平均。
17・19・20とあいだに19が出ているので、〔18と19〕の組み合わせしかない。
空欄の１つには18が入る。
残り２人の合計は、52－18＝34回
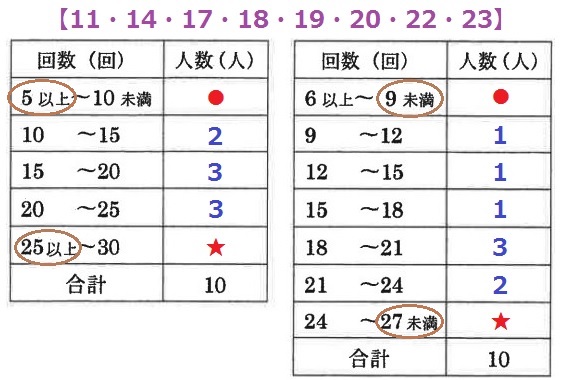
データを昇順に並べると、【11・14・17・18・19・20・22・23】
左の階級の幅は５回、右の階級の幅は３回であることに注意して、度数分布表に記入する。
すべての階級に１人以上いるから、不明の２人はそれぞれ●と★に入る。
未満を以下に変えて範囲を絞ると、●の回数は５～８回、★の回数は25～26回。
〇＋〇＝34→８＋26の組み合わせしかない。
小さい順に、８回、18回、26回。
難関中（算数科）解説ページに戻る
コメント