2017年度　開智中学過去問【算数】大問４解説

問題ＰＤＦ
次の問題に答えなさい。
（１）
下の図１のように、合同な２つの直角三角形を並べました。
（え）にあてはまる数はいくつですか。

（２）
下の図２のように、合同な２つの直角三角形を並べました。
（お）にあてはまる数はいくつですか。

（３）
下の図３のように、合同な２つの三角形を並べました。
（か）にあてはまる数はいくつですか。

＠解説＠
（１）
知りたい辺の長さを定め、それを一辺とする三角形と相似にあたる三角形を見つける。

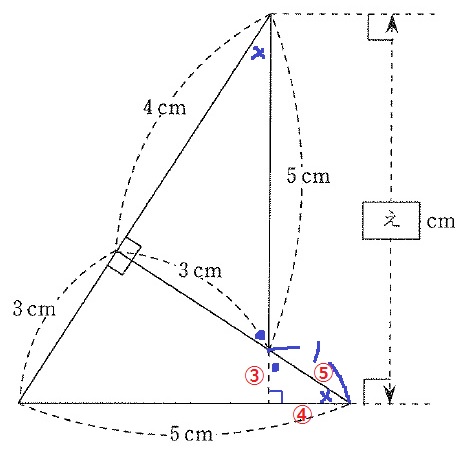
●＋×＝90°で角度を調査→内角が●－×－90°は３：４：５の直角三角形。
１×３/５＝３/５ｃｍ
（え）＝５＋３/５＝28/５ｃｍ

（２）

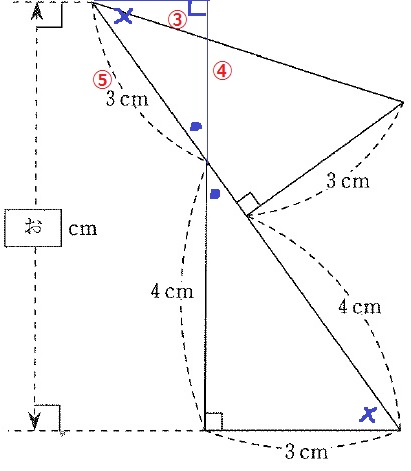
↑こんな感じに補助線をひく。
３×４/５＝12/５ｃｍ
（お）＝４＋12/５＝32/５ｃｍ

（３）

まずは角度を調査。長さが判明しているところも記入する。

２つの直角三角形をつくる。平行から下の●を錯角であげる。
下の直角三角形の内角は●－×－90°となり、辺の比は９：３＝③：①

うえの三角形で外角定理を使うと〇＋●となり、下の●をひくとあいだの角度が〇になる。
〇－△－90°の直角三角形なので、辺の比は□４：□３
（か）＝５×①/③＋９×□３/□４＝101/12ｃｍ

＠別解＠
灘入試でなんか見かけたことあるな～と思い調べてみましたら、
2012年に同じものがでており、算数星人さんが解説を書かれておりました。
以下、彼のやり方です。

蝶々型の相似をつくり、赤いところが、４×５/９＝20/９ｃｍ

続いて、２つの直角三角形の相似。
（か）＝（20/９＋９）×３/４＝101/12ｃｍ
さすが算数星人さん(´ω`)
難関中（算数科）解説ページに戻る