2020年度　早稲田実業学校中等部過去問【算数】大問５解説

問題ＰＤＦ
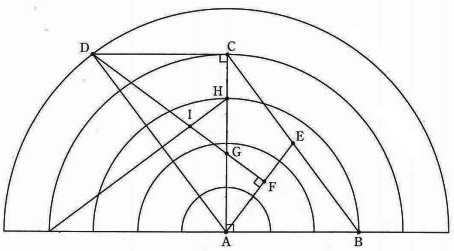
下の図の５つの半円の中心は、いずれも点Ａで、半径の比は１：２：３：４：５です。
また、四角形ＡＢＣＤは平行四辺形で、ＥＡ＝ＥＢです。次の各問いに答えなさい。

（１）
ＣＤ：ＣＧと、ＣＧ：ＧＡを求めなさい。

（２）
三角形ＡＢＣと三角形ＡＦＧの面積の比を求めなさい。

（３）
三角形ＡＢＣと三角形ＧＨＩの面積の比を求めなさい。

＠解説＠
ジーと見てると気持ち悪くなってくる…。
（１）

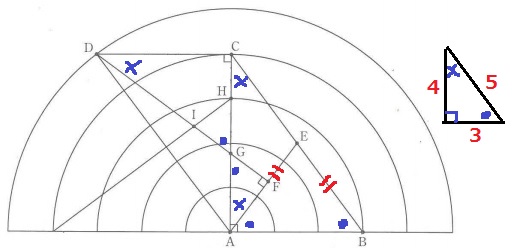
直角三角形ＡＢＣはＡＢとＡＣの長さの比が３：４。
△ＡＢＣは３：４：５の直角三角形。

∠ＡＢＣ＝●、∠ＡＣＢ＝×、●＋×＝90°で角度を調査。
二等辺三角形ＡＢＥより、∠ＥＡＢ＝●
∠ＧＡＦ＝90－∠ＥＡＢ（●）＝×
△ＡＧＦの内角で∠ＡＧＦ＝●
対頂角で∠ＣＧＤ＝●
△ＣＤＧの内角は●－×－90°となり、△ＡＢＣと相似。
→ＣＤ：ＣＧ＝３：４

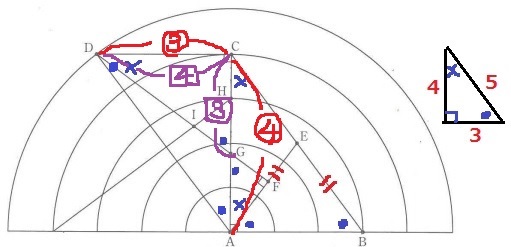
△ＣＤＡは平行四辺形ＡＢＣＤの半分で△ＡＢＣと合同。
内角は●－×－90°で、△ＣＤＡと△ＣＧＤは相似。
ＣＤ：ＣＡ＝ＣＧ：ＣＤ＝３：４
ＣＤで連比処理すると、ＣＧ＝【９】、ＣＡ＝【16】となり、
ＧＡ＝【16】－【９】＝【７】
よって、ＣＧ：ＧＡ＝９：７

（２）

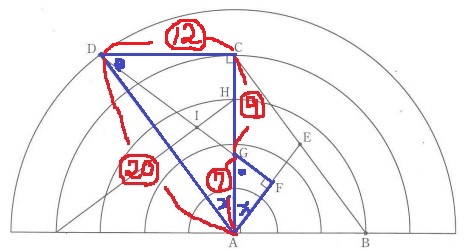
前問の連比を活用しよう。
△ＡＢＣと△ＡＣＤは合同なので、△ＡＣＤと△ＡＦＧの面積比がわかればいい。
各々内角が等しく相似。
３：４：５より、ＡＤ＝⑳
斜辺の２乗で面積比を算出。
△ＡＣＤ：△ＡＦＧ＝⑳×⑳：⑦×⑦＝400：49
よって、△ＡＢＣ：△ＡＦＧ＝400：49

（３）

△ＡＪＨに注目。
ＡＪ：ＡＨ＝４：３の直角三角形なので、△ＡＪＨの内角も●－×－90°
△ＨＧＩは二等辺三角形となる。
また、ＡＨ＝ＣＤ＝⑫より、ＨＧ＝⑫－⑦＝⑤

ＩからＡＣに垂線をひき、交点をＫとする。
二等辺三角形の頂角からおろした垂線は底辺を二等分するので、ＧＫ＝ＫＨ
ＧＨ＝⑤→ＧＫ＝〇2.5
ＡＢ：ＧＫ＝⑫：〇2.5より、
△ＡＢＣ：△ＫＩＧ＝12×12：2.5×2.5＝144：6.25
△ＧＨＩは△ＫＩＧの２倍だから、
△ＡＢＣ：△ＫＩＧ＝144：6.25×２＝288：25
難関中（算数科）解説ページに戻る