2018年度　慶應義塾中等部過去問【算数】大問７解説

問題ＰＤＦ
同じ大きさの正三角形のタイルが140枚あります。
このタイルをすき間なく並べて、正三角形または正六角形をつくります。
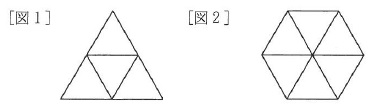
〔図１〕、〔図２〕はそれぞれ４枚、６枚のタイルを使ってつくった例です。
次の（　　　）に適当な数を入れなさい。

（１）
できるだけ大きな正三角形をつくるとき、タイルは全部で（　　　）枚使います。

（２）
できるだけ多くのタイルを使って、正三角形と正六角形を１つずつつくるとき、
正三角形をつくるのに作るタイルは（　ア　）枚、
正六角形をつくるのに使うタイルは（　イ　）枚です。

（２）

正六角形を６分割すると、〔図１〕と同じ正三角形になる。
→〔図２〕の正六角形のタイルの枚数は平方数×６枚。

〔図２〕の正六角形をつくるのに必要なタイルの枚数は、
①：１×１×６＝６枚
②：２×２×６＝24枚
③：３×３×６＝54枚
④：４×４×６＝96枚
⑤：５×５×６＝150枚…オーバー！

140枚との差を求め、残りのタイルの枚数を求める。
①：140－６＝134枚
②：140－24＝116枚
③：140－54＝86枚
④：140－96＝46枚

〔図１〕の正三角形のタイルの枚数は平方数。
先ほどの４つの数から最大の平方数との差を求め、残りの枚数を算出する。
①：134－11×11＝13枚
②：116－10×10＝16枚
③：86－９×９＝５枚
④：46－６×６＝10枚
残りの枚数が最も少ないのは③
ア（正三角形の枚数）…81枚
イ（正六角形の枚数）…54枚
難関中（算数科）解説ページに戻る