2018年度　海城中学過去問【算数】大問５解説

問題ＰＤＦ
これは、ある国のお城から魔王に連れ去られた姫を勇者が救いに行き、
もとのお城まで連れて戻ってくる冒険の物語です。
この国では格子状の道があり、行きは北か東のみ、帰りは南か西のみ動くことができます。

（１）第１の冒険
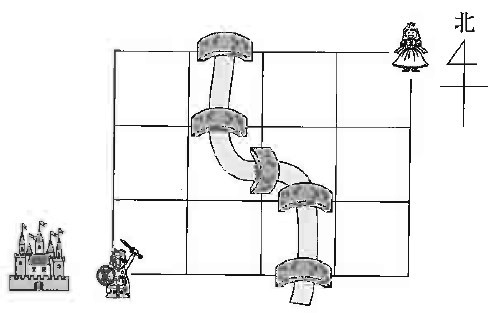
図のように街には川が流れており、橋を渡って通るしかありません。
ただし、橋は１度通るとこわれてしまい、再び通ることができなくなります。
このとき、勇者が姫を無事にお城まで連れて戻ってこられる方法は何通りありますか。

（２）第２の冒険
第１の冒険を終えた後、姫は違う街に連れ去れてしまいました。
この街で魔王は、勇者が道を１つ進むごとに、図１のＡ、Ｂ、Ｃ地点を
Ａ→Ｂ→Ｃ→Ｂ→Ａ･･･の移動を繰り返しています。
勇者がスタートするときには魔王はＡ地点にいます。
したがって、勇者が道を５つ進んだときに、魔王はＢ地点にいることになります。
勇者が魔王に出会わずに、姫を無事にお城まで連れて戻ってこられる方法は何通りありますか。

＠解説＠
こういうゲームありましたね( ˘ω˘ )
（１）
全てのケースから、壊れてしまった橋を通過するケースをひく。
まず、城から姫までの道順が何通りあるか求める。
マスの左上に数字を書き込んでもよいが、マスが多くなると大変なので順列で算出。

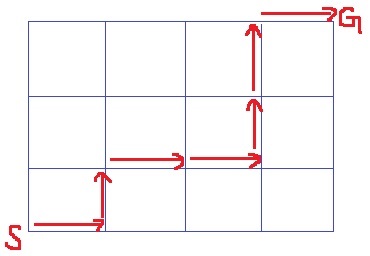
最短距離では７つの道を通過する。右４回、上３回。
→【右・右・右・右・上・上・上】の順列に相当する。
７×６×５×４×３×２×１÷（４×３×２×１）÷（３×２×１）＝35通り
行って帰ってくるので、35×35＝1225通り

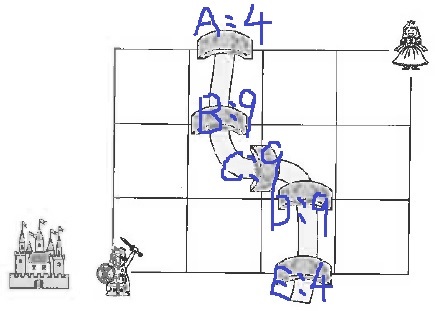
５つの橋をＡ～Ｅとする。
Ａを使うと、城から姫の往路は４通り。
復路でＡを通る場合は同じく４通りなので、往復で16通り。

同様に、Ｂ～Ｄはそれぞれ９×９＝81通り、Ｅ４×４＝16通り。
1225－（16＋81＋81＋81＋16）＝950通り

（２）
勇者だったら倒せ( ‘д’⊂彡☆))Д´)

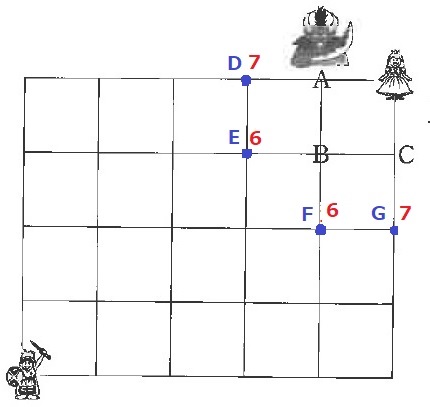
直前のポイントをＤ・Ｅ・Ｆ・Ｇとする。
Ｄは７手目。Ｄ→Ａに進むとき、魔王はＢ→Ａで鉢合わせ。
Ｅは６手目。Ｅ→Ｂに進むとき、魔王はＣ→Ｂで鉢合わせ。
ＦもＥと同様に×。
Ｇは７手目。Ｇ→Ａに進むとき、魔王はＢ→Ａだから会わない。
Ｇルートしかない。

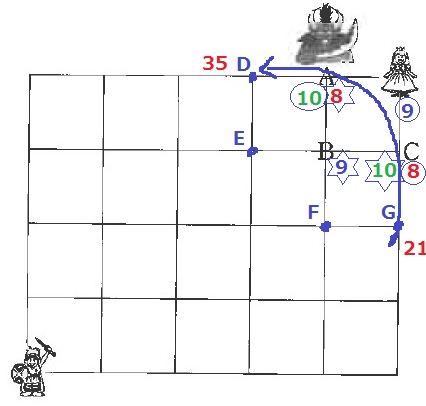
８手目〔勇者：Ｃ、魔王：Ａ〕
９手目〔勇者：姫、魔王：Ｂ〕
10手目〔勇者：Ａ、魔王：Ｃ〕
→帰りはＤを通る。

城～Ｇが21通り、Ｄ～城が35通りなので、
21×35＝735通り
難関中（算数科）解説ページに戻る

◆menu◆ 公立高校入試…関東圏メイン。千葉だけ５教科あります。％は正答率。
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→