問題ＰＤＦ
物事の処理の流れなどを表した図をフローチャート（流れ図）と言います。この問題のフローチャートでは、矢印の向きに処理を実行していきますが、条件によって、処理する内容を変えたり同じ処理を何度もくり返し実行したりすることもあります。図１、図２のフローチャートの中にあるＡやＮに、ある整数を当てはめることで処理が始まり、表示される記号はテレビなどの画面に映し出されると考えて下さい。
（１）
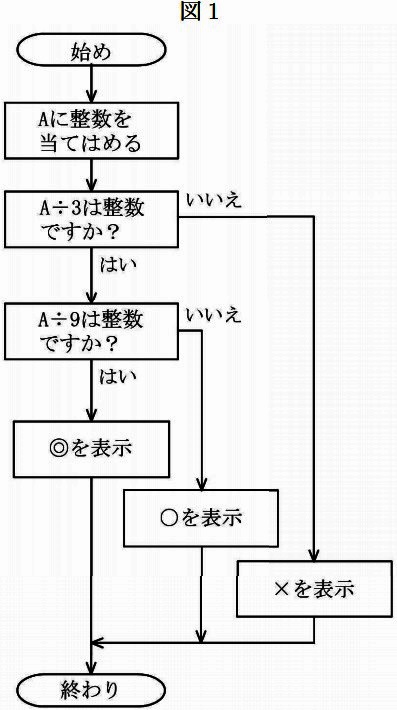
図１は、Ａに当てはめた整数がある条件を満たすかどうかを判定することができるフローチャートです、例えばＡに18を当てはめると「◎」が、６を当てはめると「〇」が、５を当てはめると「×」が表示されます。
①
Ａに3001071015を当てはめたときに、表示される記号を答えなさい。
②
異なる２つの整数をそれぞれＡに当てはめてフローチャートの処理を実行したとき、それぞれ表示された記号を確認したあと、その２つの整数の和をＡに当てはめました。次のア、イ、ウのうち、常に正しいと言えるものを、すべて選びなさい。ただし、常に正しいと言えるものがない場合は、解答らんに「なし」と書きなさい。
ア：２つの整数が両方「×」と表示されたとき、その２つの整数の和は「×」と表示される。
イ：１つの整数が「◎」、１つの整数が「〇」と表示されたとき、
その２つの整数の和は「〇」と表示される。
ウ：２つの整数が両方「〇」と表示されたとき、その２つの整数の和は「〇」と表示される。
（２）
図２は、Ｎに当てはめた整数がある条件を満たすかどうかを判定することができるフローチャートです。フローチャートの中のＫには、始めに２を当てはめます。そのあとの処理でＫの値は１ずつ大きくなっていきます。
①
Ｎに51から60までの整数10個をそれぞれ当てはめたとき、
「〇」と表示される整数をすべて答えなさい。
②
Ｎに２つの連続する整数ａ、ｂ（ｂはａより１だけ大きい数）をそれぞれ当てはめます。例えば、連続する整数とは「80と81」のような２つの数のことを指します。すべての整数において、２つの連続する整数が両方とも「〇」と表示されるのはただ１組しかありません。その２つの連続する整数を「80と81」のように答えなさい。
③
３よりも大きい整数のうち、３つの連続する整数ａ、ｂ、ｃ（ｂはａより１大きく、ｃはａより２大きい整数）をそれぞれＮに当てはめたとき、ａとｃは「〇」と表示され、ｂは「×」と表示されました。この条件を満たす３つの連続する整数は、どんなときでもまん中のｂが必ず〔 〕の倍数になります。〔 〕に当てはまる最も大きい整数を答えなさい。
＠解説＠
（１）①
３の倍数→位の和が３の倍数
９の倍数→位の和が９の倍数
3001071015は３の倍数かつ９の倍数なので◎。
②
文章になおしてみよう。
ア：『３の倍数でない２つの整数の和は、必ず３の倍数でない』
→反例を１つ挙げればいい。１＋２＝３がある。×
イ：『９の倍数と、９の倍数でない３の倍数の和は、必ず９の倍数でない３の倍数である』
→９の倍数と９の倍数でない整数の和は、９の倍数にはならない。
また、９の倍数は３の倍数なので、９の倍数と９の倍数でない３の倍数の和は３の倍数となる。○
ウ：『９の倍数でない３の倍数である２つの整数の和は、必ず９の倍数でない３の倍数である』
→３＋６＝９がある。×
すべて式だが、答えはイのみ。
（２）
先に”ある条件”を捉えておきたい。
簡単に直すと…
最初は、Ｎ≧２、Ｋ＝２。
Ｋ≧Ｎ（ＫがＮ以上）であれば○。
Ｋ＜Ｎ（ＫがＮ未満）であれば、Ｎ÷Ｋをする。
商が整数だと×。
整数にならないと、Ｋ＋１をして再度、ＫとＮの大小関係を比べ、
Ｋ＜Ｎ→Ｎ÷Ｋ→商が整数にならないとＫ＋１をしてループ処理をする。
Ｋ≧Ｎであれば○が確定し、すぐに処理が終わる。
Ｋ＜Ｎであれば割り算をし、割り切れないとＫの値はどんどん大きくなっていく。
つまり、割り切れない回数が増えるたびに、Ｋの値が１ずつＮに近づいていき、
Ｋ＝Ｎとなれば○と表示される。
ということは、○が表示される数は、÷２、÷３、÷４、÷５…
÷（Ｎ－２）、÷（Ｎ－１）をしても割り切れなかった数、すなわち、素数。
図２は素数判定のフローチャートとなる。
51～60までの素数は、53と59。
②
素数が２つ連続する場所。
整数は奇数・偶数・奇数・偶数…の繰り返しで、偶数は２で割り切れるので、
素数が２連続になるところがなさそうだが、１ヶ所だけある。
それは、「２と３」。
③
連続する３つの整数ａ、ｂ、ｃで、ａとｃが素数である場合、
真ん中の数ｂが何の倍数であるかを求める。
整数は奇数・偶数…の繰り返しで、素数は奇数だからｂは偶数（２の倍数）。
連続する３つの整数には必ず３の倍数が含まれるので、
ａ・ｃが素数であるということは、残りのｂが３の倍数となる。
すなわち、ｂは２の倍数であり、かつ３の倍数だから、６の倍数となる。
*『３よりも大きい整数』なので、ａに４以上をあてはめて探してもいい。
＠双子素数＠
（３・５）のように、差が２である素数のペアを双子素数という。
双子素数のあいだの数は、解説のとおり、必ず６の倍数となり、
双子素数のペアは６の倍数－１と６の倍数＋１となる。
双子素数が無限個あるかどうかは、未だ証明されていない。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント