問題ＰＤＦ
栄くんは次の問題に取り組んでいます。
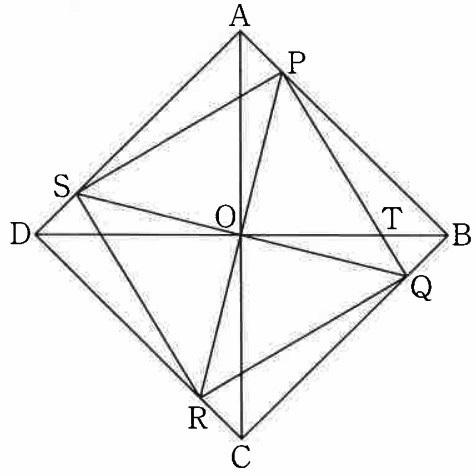
栄くんが悩んでいると、東さんが「三角形ＯＡＢと合同な三角形をあと３つ用意して、
敷き詰めてみたらどうかな？」と言って、次の図をかいてくれました。
（１）
東さんがかいた図において、三角形ＯＰＱの面積を求めなさい。
（２）
栄くんが取り組んでいた問題に答えなさい。
（３）
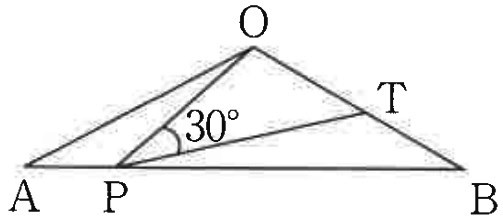
角ＯＡＢ＝120°、辺ＡＢ＝５ｃｍの二等辺三角形ＯＡＢの辺ＡＢ上にＡＰ＝１ｃｍ、ＰＢ＝４ｃｍとなる点Ｐをとり、辺ＯＢ上に角ＯＰＴ＝30°となる点Ｔをとります。このときＯＴとＴＢの長さの比をもっとも簡単な整数の比で答えなさい。
＠解説＠
（１）
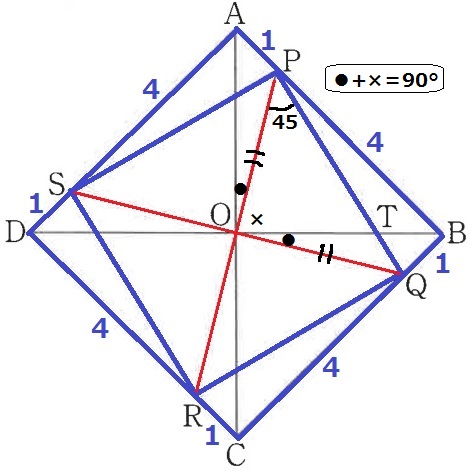
合同よりＯＰ＝ＯＱ、●＋×＝90°から∠ＰＯＱ＝90°
△ＯＰＱは直角二等辺三角形で、これを４つならべた四角形ＰＱＲＳは正方形。
正方形ＡＢＣＤから外側の４つの直角三角形をひくと正方形ＰＱＲＳで、
これを４等分すると直角三角形ＯＰＱとなる。
（５×５－１×４÷２×４）÷４＝17/４ｃｍ2
（２）
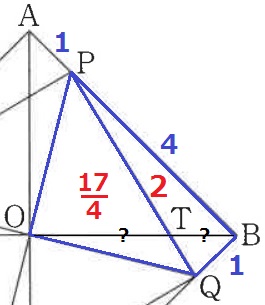
△ＯＰＱと△ＢＰＱに着目する。
底辺がＰＱで共通するので、高さの比がＯＴ：ＴＢにあたる。
ＯＴ：ＴＢ＝△ＯＰＱ：△ＢＰＱ＝17/４：２＝17：８
（３）
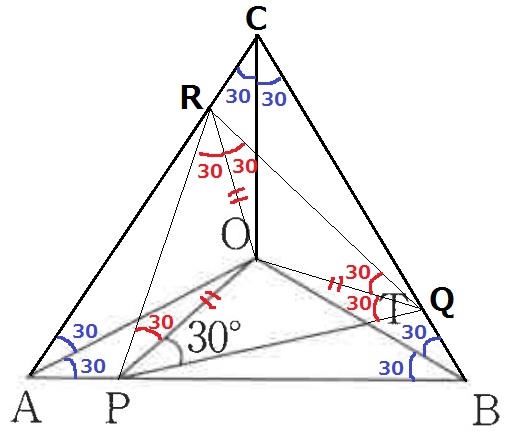
前問の誘導にしたがって合同図形を敷き詰める。
二等辺ＯＡＢは底角が30°。
これを３つ敷き詰めると３つの内角が60°だから△ＡＢＣは正三角形。
合同でＯＰ＝ＯＱ、△ＯＰＱは底角が30°の二等辺⇒同様に△ＰＱＲも正三角形。
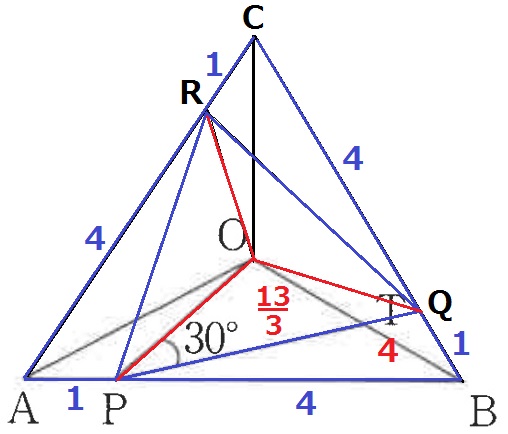
ＯＴ：ＴＢは底辺ＰＱが共通ゆえ、△ＯＰＱと△ＢＰＱの高さの比に相当する。
面積比で対処する。
△ＢＰＱ…４×１＝４
△ＯＰＱ…（△ＡＢＣ－外側の３つの三角形）÷３＝（５×５－４×１×３）÷３＝13/３
ＯＴ：ＴＢ＝13/３：４＝13：12
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント