問題ＰＤＦ
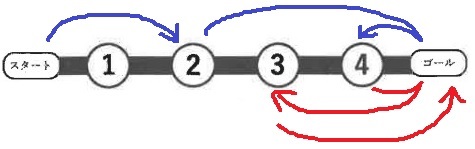
図１のようなすごろくと、１、２、３、４のいずれかの目が出るルーレットがあります。
スタートにあるコマを、以下のルールで、ゴールにぴったり止まるまで動かします。
●ルーレットを回して出た目の数だけ右に動かします。
●ゴールにぴったり止まれない場合は、ゴールで折り返して、
余った分だけ左に動かします。
●折り返した後も、次にルーレットを回したとき、まずは右に動かします。
●一度止まった①～④のマスは「スタートに戻る」マスになり、
次以降にそのマスに止まった場合は、コマをスタートに戻します。
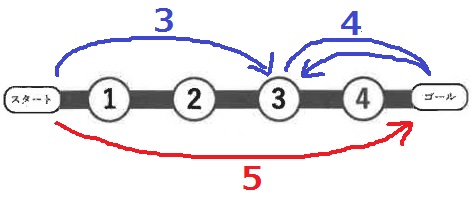
例えばルーレットの目が１、３、４の順に出たとき、コマは、①マス、④マスの順に止まった後、
ゴールで折り返して②マスに止まります（図２）。
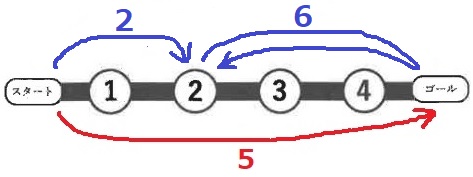
続いて、ルーレットの目が１、１の順に出ると、コマは、③マス、④マスの順に止まり、
④マスはすでに「スタートに戻る」マスになっているので、スタートに戻ります（図３）。
これ以降、ルーレットでどの目が出てもスタートに戻ることになり、ゴールできません。
（１）
ルーレットで３と４の目が出ることなくゴールしました。
（ア）スタートに戻ることなくゴールしたとき、考えられる目の出方は何通りありますか。
（イ）ゴールするまでに出た目の和として考えられるものを、小さい方から３つ答えなさい。
（２）
ルーレットで１と２の目が出ることなくゴールしました。
（ア）スタートに戻ることなくゴールしたとき、
ゴールするまでに出た目の和として考えられるものをすべて答えなさい。
（イ）ゴールするまでに出た目の和が2022のとき、何回ルーレットを回しましたか。
（３）
スタートに戻ることなくゴールしました。
このとき、ゴールするまでに出た目の和として考えられるものをすべて答えなさい。
（４）
ゴールしたとき①～④のすべてのマスが「スタートに戻る」マスになっていて、
ゴールするまでに出た目の和は12でした。
このとき、考えられる目の出方は何通りありますか。
＠解説＠
（１）ア
１か２しか進まず、スタートに戻らない。
⇒出た目の和が５になればいい。
（１、１、１、１、１）→１通り
（１、１、１、２）→４通り
（１、２、２）→３通り
合計で８通り。
イ
和が最も少ない場合は前問の５。
折り返すことなく、ストレートにゴールすればいい。
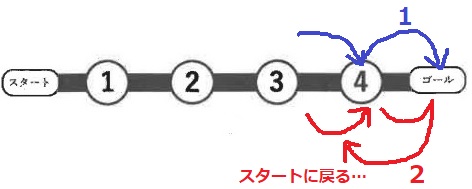
和を５より大きくするにはゴールで折り返す。
④マスで１を出すとそのままゴール、２を出すと折り返してスタートに戻る。
和を増やすには、④で止まってスタートに戻るマスにして、折り返して④でスタートに戻る。
再スタートから③に止まり、２を出せばゴール。
折り返しの④までが６。再スタートで＋５して11。
【例】Ｓ（スタート）→②→④→④→Ｓ→①→③→Ｇ（ゴール）
次に和が大きくなるルートは、スタートに戻ったあとにまたスタートに戻る。
２周目にマス①でスタートに戻れたら和を小さくできるが…
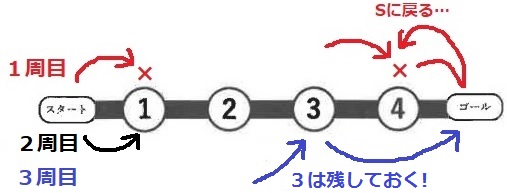
１周目に①に止まる。どうにかして④まで行き、２を出して④、スタートへ戻る。
２周目は①に止まってスタートへ。
３周目は③で２を出して④を飛び越えないとゴールできない。
すなわち、１周目ではゴール用にマス③を残しておく！（③に止まらない）
そうなると、１～２周目は①→②→④→④→Ｓ→①→Ｓの流れになるが
①と②が潰されているので、３周目で③に行けない！
２周目に①でスタートに戻るプランは潰された。
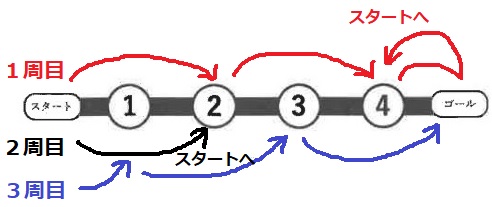
１周目で②に止まり、２周目で②でスタートに戻るとできる。
和は６＋２＋５＝13
答えは小さい順に５、11、13。
（２）ア
３か４しか出せない。和が５にならないのでストレートにゴールできない。
フィニッシュの仕方から考える。②で３を出せばゴールに行ける。
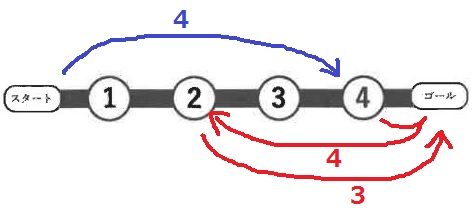
②に着くには④で４を出すしかない。
和は11。
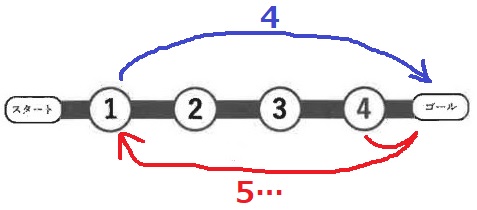
①から４でフィニッシュしようとしても、５を出さないと①にたどり着けない。
②からフィニッシュするしかない。
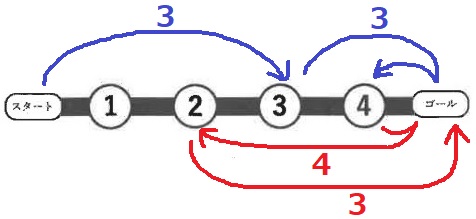
④にたどりつく別のルートを探す。
１周目で③に迂回して④を目指す。
和は13。
他にないか探してみる。
最後が〔④→②→Ｇ〕。３か４のみで④にたどり着く方法がもう無い。
よって、11と13。
まだ３問目だがキツイ(´д｀)
イ
スタートに戻らなければ、この２通りしかなかった。
最後は〔④→②→Ｇ〕が確定だから、ゴール用に②と④は残しておかなければならない。
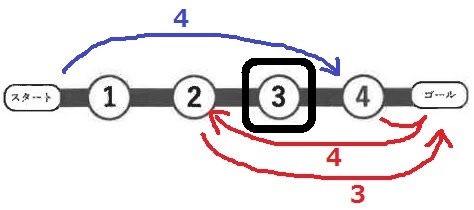
３か４しか進めない状況でどうにかするにはココしかない！
つまり、スタートから３進んで③、③がスタートに戻るマスになる。
４を出して③に戻り、スタートに戻る。スタートから３進んで③でスタートに戻る…
以下、ひたすら３を出し続けて、スタートと③を往復する。
最後に〔④→②→Ｇ〕でフィニッシュ！
出た目でまとめると、【３→４】【３→３→…（ループ）…→３】【４→４→３】
2022から最初と最後の５回分の出目を引く。
2022－（３＋４＋４＋４＋３）＝2004
ループの３の回数は、2004÷３＝668回
ルーレットの回数は、668＋５＝673回
（３）
（１）（２）アより、５と11と13は手堅くゲット。
他にないだろうか？
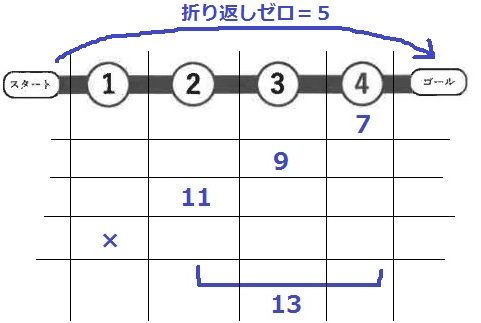
ゴールからの折り返し分で増えていくので、どこまで折り返すかで場合分けしてみる。
④は７、③は９、②は11。①までは折り返せないので×。
②と④の折り返しが13であった。
残りの候補としては〔②と③と④〕と〔②と③〕と〔③と④〕
〔②と③〕は無い！
②から折り返して③は５マス、③から折り返して②も５マスだから不可能。
〔②と③と④〕も無い！
折り返し後の着地点を③→④→②や②→④→③と④をクッションに挟もうとしても無理。
〔③と④〕はどうか？
できるけど和が既出の11。
よって、答えは５、７、９、11、13です。
（４）
この大問だけで試験時間終わりそうなのだが(ꐦ°᷄д°᷅)
具体的にどのマスに止まったかは後回しにして、先に和が12になるルートを把握する。
（３）より、スタートに戻ることがないとすると、
５・７・９・11・13と連続する５つの奇数になっている。
和が12ということは、どこかのマスを２回踏んでスタートに戻るしかない。
２周目がストレートゴールだとすると、１周目は12－５＝７移動する。
スタートから７マス移動してゴールから折り返すと③。
１周目で③で止まってスタートに戻るマスにして、折り返して③でスタートに戻る。
方針１；【③③】の固まりを作る。最終的に全部のマスへ止まるようにする。
●Ｓ【③③】Ｓ①②④Ｇ
●Ｓ①【③③】Ｓ②④Ｇ
●Ｓ②【③③】Ｓ①④Ｇ
●Ｓ①②【③③】Ｓ④Ｇ
方針２；１周目の③→③のあいだで④を挟むことができる。
２周目は①か②から直接ゴールへ飛ぶ。【③④③】の固まりを作る。
●Ｓ【③④③】Ｓ①②Ｇ
●Ｓ①【③④③】Ｓ②Ｇ
●Ｓ②【③④③】Ｓ①Ｇ
＊Ｓ①②【③④③】ＳＧはできない。
２周目でＳからＧに直接ジャンプができないため。
先ほどは③でスタートに戻るだった。②で戻るはどうか？
和が13になるのでダメです！×
④で戻るはどうか？
１周目で和が６。残りは６。
ＳからＧまで５だから、どこかで１つ暇を潰さなくてはならない。
プランとしては…１周目で①に止まり、スタートに戻るマスにする。
④に止まり、ゴールを折り返して④に止まり、スタートへ。
２周目は①に止まってスタートへ。
３周目は②か③を踏み台にしてゴールへ向かう。
方針３；１～２周目で〔①④④①〕の固まりを作る。
●Ｓ①④④Ｓ①Ｓ②③Ｇ
方針４；〔①④④①〕の並びを維持して、１周目で②か③を踏む。
●Ｓ①②④④Ｓ①Ｓ③Ｇ
●Ｓ①③④④Ｓ①Ｓ②Ｇ
＊１周目でＳ①②③④④Ｓと全部踏むと３周目でゴールできない。
もう無いと祈る。
10通り。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント