問題ＰＤＦ
視覚障がい者が、指先の触覚により文字や文章を読み取れるように、６点式点字が用いられています。６点式点字では、下の図のようにマス内にＡ～Ｆの６点について、突起（以下●と表す）と平面（以下〇と表す）を組み合わせることで１つの文字表します。
渋男と教子さんが、駅の自働券売機の前で点字について会話をしています。
次の会話文を読み、〔 あ 〕～〔 け 〕にあてはまる数を答えなさい。
渋男：運賃表にある、このボコボコしてるの、何だろう？
教子：これはね、点字といって、目の不自由な人が指先の触覚で
文字が読み取れるようにしているんだよ。私ね、点字のことは勉強したことがあるんだ。
渋男：そうなんだ。僕は初めて知ったよ。
よく見てみると、縦に３つ、横に２つの６つの点で１セットになっているみたいだね。
教子：そうなの。日本で使われている点字は『６点式点字』といって、上の図のように
マス内のＡ～Ｆの６点について、●と〇を組み合わせることで１つの文字を表しているんだよ。
渋男：なるほど。６点全部が〇のときは文字にならないから除くとして、
全部で〔 あ 〕通りを表せるよね。
教子：その通り。でも、目の不自由な人がその全てを区別できるかしら。
まずは、●が１点のときから考えて見ましょう。さっきの〔 あ 〕通りは、
下の図の＜ア＞～＜カ＞はそれぞれ異なる文字を表すこととして考えたよね。
渋男：そうだね。
教子：でも、上の図の＜ア＞～＜カ＞はいずれもマスの中に●が１点なので区別が難しいから、
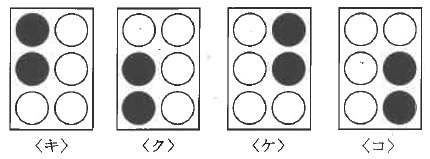
実際にはどれも同じ文字を表すことになるの。同じように、次の図の＜キ＞～＜コ＞は、
マスの中に●が２点あって、その２点の位置関係が同じだから、４つとも同じ文字を表すの。
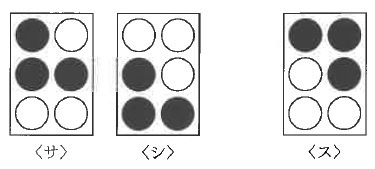
渋男：分かった。ということは、下の図の＜サ＞、＜シ＞も、マスの中に６点のうち３点が●で、
３点の位置関係が同じだから、同じ文字を表すことになるね。
でも、＜ス＞は別の文字を表すんだね。
教子：そういうこと。これ以降は、＜サ＞と＜シ＞のように、
●の数が同じでその位置関係も同じものは同じ文字として扱うとしましょう。
では、まず数字から考えてみよう。
数字を点字で表すときは、１マスの６点のうち、Ａ～Ｄの点だけが使われるんだけど、
この４点だけを使うと、１マスで何通りの文字が表せるかしら。
渋男：これは地道に数えていくしかないのかな。
４点のうちの１点が●のときは１通り、４点のうちの２点が●のときは〔 い 〕通り、
４点のうちの３点が●のときは〔 う 〕通り、４点のうちの４点が●のときは１通りで、
全部で〔 え 〕通りだ！
教子：そうだね。これだけあれば、０～９の全ての数字を１マスで表せることになるね。
じゃあ、次にひらがなのことも考えてみよう。ひらがなを点字で表すときは、
Ａ～Ｆの６点すべてを使われるのだけど、数字で考えたものも含めて何通りあるか。
同じように考えて見ましょう。
渋男：少し大変になるね。６点のうちの１点が●のときは１通り、
６点のうちの２点が●のときは〔 お 〕通り、６点のうちの３点が●のときは〔 か 〕通り、
６点のうちの４点が●のときは〔 き 〕通り、６点のうちの５点が●のときは〔 く 〕通り、
６点のうちの６点が●のときは１通りで、全部で〔 け 〕通りだ！
教子：がんばったね。
渋男：でもこれだと、数字と重複するものもあるし、
ひらがな全種類表すことができないんじゃないかな。
教子：鋭いところに気付いたね。実際には、数字が始まる前には『数字が始まる』という意味の
点字が入るし、『ん』の文字は１文字目に来ることがないから、他の文字と同じだったりして、
上手く作られているらしいわ。
渋男：そうなんだ！それはおもしろいね。点字も奥が深そうだね。
＠解説＠
あ…１つの点は●か〇の２通り。点は６つで、すべて〇の場合を除く。
２×２×２×２×２×２－１＝63通り
い…４マスに２点。
位置関係が重複しないようにする。４通り
う…４マスに３点。
使わない１マスを選んで４通り。（どれも形はかぶらない）
え…１＋４＋４＋１＝10通り
お…６マスに２点。
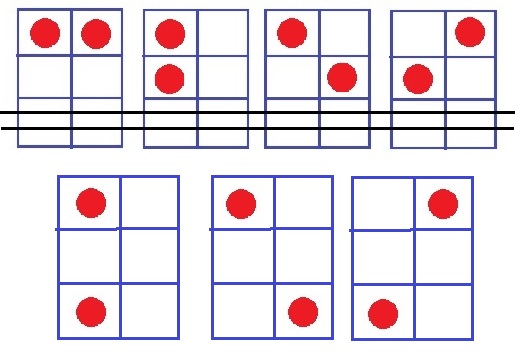
先ほどの４通りに３段目を追加する。
４＋３＝７通り
か…６マスに３点。
上２段の３点は４通りだった。これに加えて、３段目を使うケースを考える。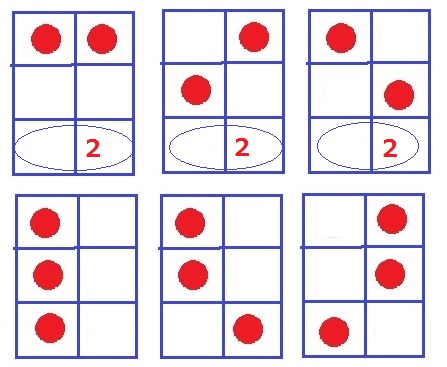
〔 い 〕より上２段の２点の位置は４通り。
気をつけるべき点は、上２段の●が縦に並んだときは３通りできること！
計９通り。
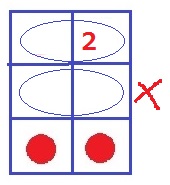
さらに３段目に２つあるケース。
２段目にもう１つを入れてしまうと、上２段だけでつくったパターンとかぶってしまう。
距離を開け、１段目の左右で２通り。
４＋９＋２＝15通り
き…６マスに４点。
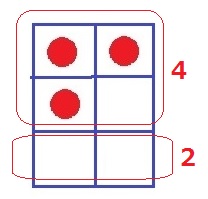
上２段が４通り。
残り１つを３段目の左右のどちらかに配置して２通り。
４×２＝８通り
３段目に２つを固定。
すると、同じ形を上下１段ズラせても、左右を入れ替えても別の形になるので、
４マスから２つ選ぶ組み合わせと同じ→4Ｃ2＝６通り
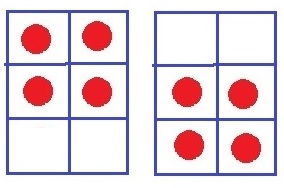
３段目を使わない場合（上２段４マスが●）は、すでにカウント済み。
８＋６＝14通り
く…６マスに５点。
使わない１マスを選んで６通り。
け…１＋７＋15＋14＋６＋１＝44通り
難関中（算数科）解説ページに戻る
コメント