問題PDF
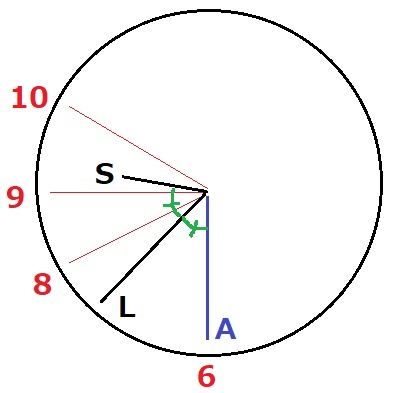
次の図のように、長針をL、短針をS、6を指す動かない針をAとする時計があります。この時計の短針は時計回りに動きますが、長針は壊れており、反時計回りに動きます。ここで、SとLが作る角をAが二等分する状態をXとします。状態Xとなる例は次のような場合です。

同様にLとAが作る角をSが二等分する状態をY、AとSが作る角をLが二等分する状態をZとします。このとき、次の問いに答えなさい。
(1)
8時から時計を動かしたとき、はじめて状態Xになるのは何分後か答えなさい。
(2)
8時から90分間時計を動かしたとき、
状態X、Y、Zはどのような順で起こるか次の例のように答えなさい。
【例】X、Y、Z、Xの順で起こるとき、X→Y→Z→X
(3)
8時から時計を動かしたとき、2回目の状態Zになるのは何分後か答えなさい。
@解説@
(1)
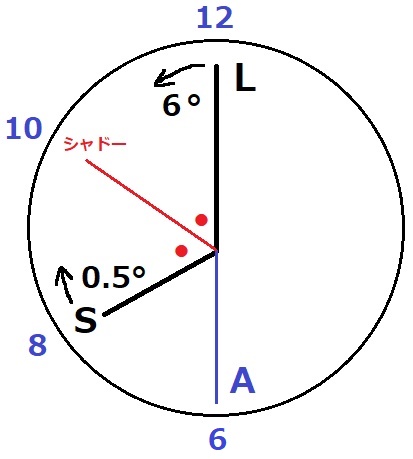
常にLとSの中間に位置するシャドーをつくる。
1分あたり長針Lは反時計周りに6°、短針Sは時計周りに0.5°。
シャドーの速さはLとSの平均。
6-0.5°=5.5°反時計回りが大きい→5.5÷2=11/4°反時計回り
シャドーがAと重なれば、SとLが作る角をAが二等分する状態になる。
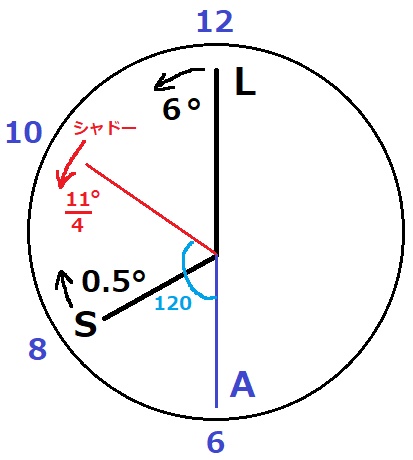
8時にシャドーは文字盤で10→Aとシャドーは120°離れている。
120÷11/4=480/11分後
(2)
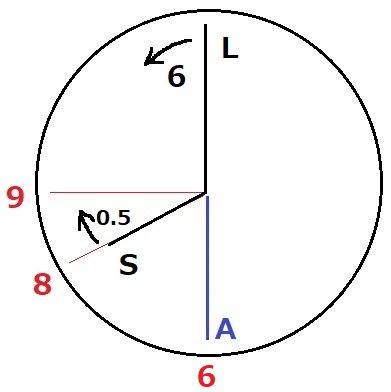
大変:;(∩´﹏`∩);:
幸い、何時何分かは答えなくていいので、針の動きを追って状態を調べていく。
Aは固定。Sは最初の1時間は8~9の間にしかいない。Lの進みが一番速い。
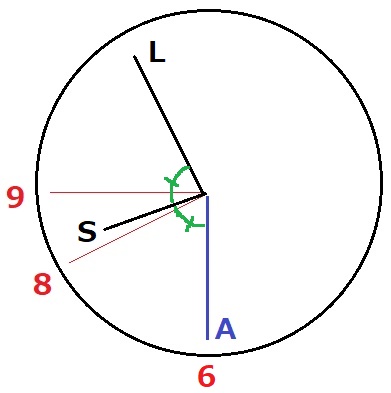
まず、SがLとAのあいだに入る。【Y】
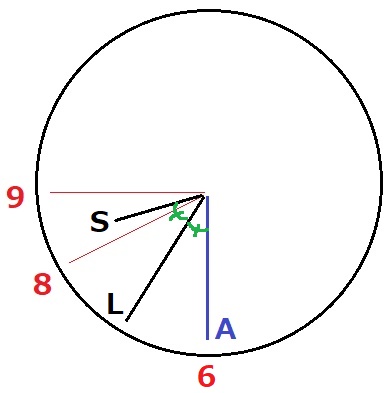
SとLが重なった後、LがSとAのあいだにくる。【Z】
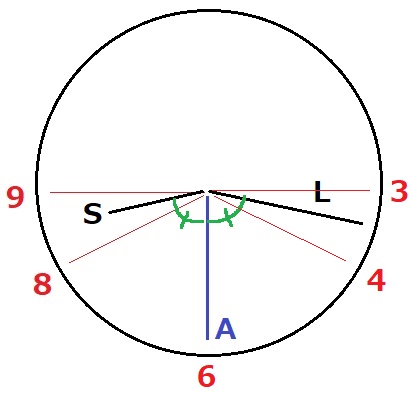
LがAを追い越し、Sと左右対称の位置にくるとAがあいだにくる。【X】
(1)より480/11分後の状態。
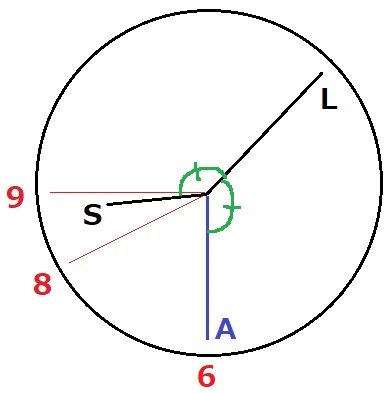
これが見えづらい。
先の状態からLとSがなす大きい方の角だけが小さくなっていく。
すると、Lが角の二等分線になる。【Z】
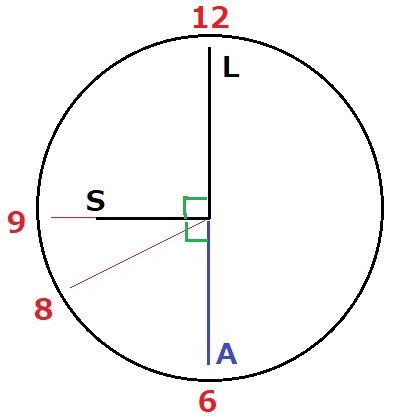
9時で直角になる。【Y】
LがSと出会った後、SとAのあいだにくる。【Z】
LがAと重なって90分経つ。
Y→Z→X→Z→Y→Z
(3)
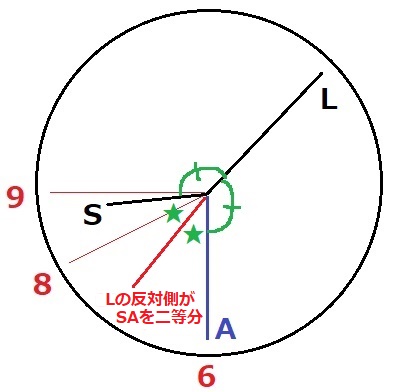
この時刻を求める。
Lを反対側に延長すると、これを軸としてSとAが対称関係にある。
Lの反対側の線がSとAの角を二等分する。
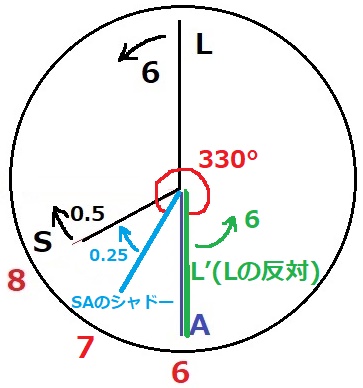
SAを二等分するシャドーと、Lの反対側のL’が出会う時間を求めればいい。
シャドーは文字盤で6と8のあいだの7。
速さはSとAの平均→0.5÷2=0.25
L’は6からスタートする。
8時では330°離れており、1分あたり6+0.25=6.25°近づくから、
330÷6.25=52.8分後



コメント