問題PDF
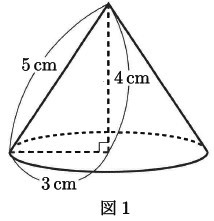
図1のような円すいがあります。
いま、図2のように円すいの底面の中心が平面上の点Aに重なるように、円すいを置きます。
円すいを矢印の方向に、底面の中心が点Bに重なるまで直線AB上を動かします。
点Aと点Bの間は10cmです。

(1)
円すいを動かしてできる立体の体積を求めなさい。
(2)
円すいを動かしてできる立体の表面積を求めなさい。
@解説@
(1)

円錐を半分に割った断面の二等辺三角形が移動したと考えれば、
あいだは三角柱になると想像しやすい。
両サイドはセットにして1つの円錐にする。
6×4÷2×10+3×3×3.14×4÷3
=120+37.68=157.68cm3
(2)
【円錐の側面積=半径×母線×3.14】
3×3×3.14+3×5×3.14+(6+5+5)×10
=24×3.14+160
=235.36cm2



コメント