問題ＰＤＦ
ある星では、１日が８時間で、１時間が40分です。
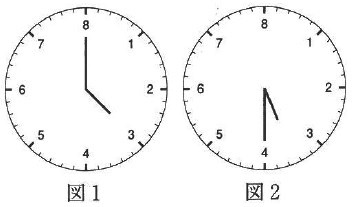
この星の時計は下の図のようになっており、例えば、図１は３時ちょうど、
図３は３時20分を表しています。次の問いに答えなさい。
（１）
３時32分のとき、長針と短針がつくる角のうち、
小さい方の角の大きさは何度ですか。
（２）
長針と短針のつくる角の大きさが90°となるのは１日で何回ありますか。
（３）
現在４時16分です。次に長針と短針のつくる角の大きさが128°となるのは何分後ですか。
＠解説＠
（１）
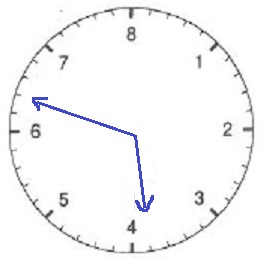
３時32分を描いてみる。
32/40＝４/５なので、短針はちょうど目盛りを指す。
これさえわかれば、目盛りを数えるだけで解けてしまう。
360×13/40＝117°
＠＠＠
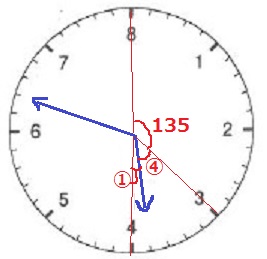
時計算っぽく計算するのであれば、
長針が動いた角度は、360×32/40＝288°なので、
288－135－45×４/５＝117°
（２）
普通の時計と同じ考えで良いと思う。
普通の時計は短針が１周する12時間、厳密にいえば０時00分～11時59分のなかで、
長針と短針が重なる回数は11回（11時59分の１分後の０時00分はカウント済み）。
長針と短針が直角となるのは、２本の針が重なるタイミングの前後に発生するので、
12時間では11×２＝22回発生する（24時間では44回）。
１日が８時間の世界では、長針と短針が重なる回数は７回。
よって、直角になる回数は７×２＝14回
（３）
典型的な旅人算。
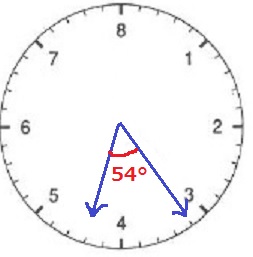
16/40＝２/５
４時16分の短針は目盛りを指す。
６目盛り差なので、あいだの角度は360×６/40＝54°
１分あたり長針は360÷40＝９°、短針は360÷８÷40＝９/８°進む。
１分あたり、９－９/８＝63/８°差がつまる。
よって、（54＋128）÷63/８＝208/９分後
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント