問題ＰＤＦ
図のように、立方体ＡＢＣＤＥＦＧＨがあります。
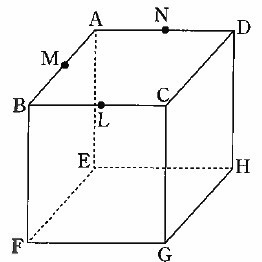
点Ｌ、Ｍ、Ｎは、それぞれ辺ＢＣ、辺ＡＢ、辺ＡＤの真ん中の点です。
次の問いに答えなさい。
（１）
この立方体の辺の上や頂点に点Ｐをとります。
三角形ＡＢＰが二等辺三角形になるような、点Ｐのとり方は何通りありますか。
（２）
この立方体を、３つの点Ｌ、Ｎ、Ｇを通る平面で切ったとき、２つに分かれた立体の表面積の差は、もとの立方体の表面積の〔 ア 〕倍です。また、２つに分かれた立体の体積の差は、もとの立方体の体積の〔 イ 〕倍です。ア・イにあてはまる数をそれぞれ求めなさい。
（３）
この立方体の１辺の長さを６ｃｍとします。この立方体を３つの点Ｍ、Ｎ、Ｇを通る平面で切ったとき、切り口の形は〔 ウ 〕です。頂点Ａを含む方の立体の体積は〔 エ 〕ｃｍ3です。
ウにあてはまる図形を次の①～④から選び、エにあてはまる数を答えなさい。
①三角形 ②四角形 ③五角形 ④六角形
＠解説＠
（１）
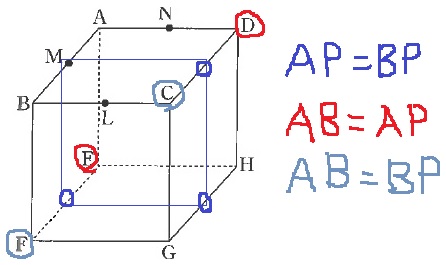
二等辺三角形の３辺のうち、どことどこの辺が等しくなるか。
３つのパターンに場合分けしよう。
ＡＰ＝ＢＰは、上の青枠の面上にくるとき。
Ｍは直線ＡＢ上になので三角形ができない。
７通り
（２）
まずは、切断された２つの立体の表面積の差を求める。
同じ面積は相殺する。
四角形ＡＢＦＥ＝四角形ＤＣＧＨ
四角形ＡＢＬＮ＝四角形ＮＬＣＤ
四角形ＬＧＨＮ（切断面）
差が生まれるのは、前後と底面だけ。
ＢＬの長さを１とすると、立方体の１辺は２。
四角形ＢＦＧＬ：四角形ＬＧＣ＝１＋２：１＝③：①
（高さが等しいので、上底＋下底で面積比を求める）
差は②で、前後の合計の差は④
底面は２×２＝④
差の合計は⑧
立方体の表面積は２×２×６＝㉔
⑧/㉔＝１/３倍
ア…１/３
＠＠
体積はもっと簡単。
柱体なので、体積比は四角形ＢＦＧＬ：四角形ＬＧＣ＝③：①
→差は②
立方体の体積は④なので、②/④＝１/２倍
イ…１/２
（３）
ダイヤモンド型になる→③五角形
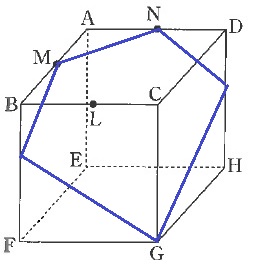
Ａを含む方の体積を求める。
Ａ側をダイレクトに求めることもできるが、延長したときに３つ外にでるので、
Ｃ側を求めてから、あとで立方体から引く。
△ＭＡＮ∽△ＯＤＮ→辺の比は１：１
ここからＯＤ＝３ｃｍ
△ＯＤＩ∽△ＧＨＩ→辺の比は１：２
ここから、ＤＩ＝２ｃｍ
以上の関係はＰ方面でも同様である。
Ｃ側の体積は、
９×９÷２×６÷３－３×２÷２×３÷３×２
＝81－６＝75ｃｍ3
よって、Ａ側の体積は、６×６×６－75＝141ｃｍ3
難関中（算数科）解説ページに戻る
コメント