問題ＰＤＦ
図のような２つの容器Ａ、Ｂがあります。外側の容器Ｂの高さは容器Ａの高さの1.2倍です。容器Ａと容器Ｂの底面の半径の比は１：２です、容器Ｂには、容器Ａの高さの２/３のところに排水口がついていて、毎分1.2リットルの水が排水されます。グラフは、空の容器Ａに水を毎分2.4リットルで入れたときの水面の高さ（ＡとＢの高い方）を表したものです。
グラフのＣは〔 〕、Ｄは〔 〕です。
＠解説＠
ＡとＢの高さの比は５：６。
底面積の比は、Ａ：Ｂ＝１：（２×２－１）＝１：３
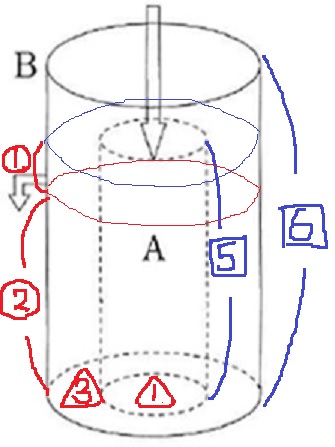
Ｃは高さ□５まで水に満たされたとき。
Ａは底辺△１、高さ□５で、体積は【５】
【５】を埋めるのに11分かかる。
高さ□５までのＢの体積は、△３×□５＝【15】
もし、排水がなかったら、11×【15】/【５】＝33分かかる。
しかし、この３分の１は排水（毎分1.2Ｌ）により給水（毎分2.4Ｌ）の効率が半分に落ちる。
つまり、３分の１については時間が２倍かかる。
排水で追加される時間は、33×１/３＝11分
Ｃ＝11＋33＋11＝55分
もし、排水がないと、給水開始～高さ□５までは11＋33＝44分でおわる。
高さ□１を埋めるのに、44×□１/□５＝8.8分かかる。
実際は排水により２倍の時間がかかるので、高さ□１は8.8×２＝17.6分かかった。
Ｄ＝55＋17.6＝72.6分
難関中（算数科）解説ページに戻る
コメント