問題PDF
生徒が25人いるクラスで10点満点の試験を行いました。試験は1番、2番、3番の3問からなり、配点は1番が2点、2番が3点、3番が5点です。部分点はありません。
試験の結果、2番を正解した生徒は全部で14人、3番を正解した生徒は全部で14人いました。また、3問中ちょうど2問正解した生徒は全部で16人おり、その16人の得点の平均は6.5点でした。3問中ちょうど1問正解した生徒の得点の平均は3.5点でした。クラス全体の得点の平均は5.68点でした。得点が0点の生徒はいませんでした。
(1)
1番を正解した生徒の人数を求めなさい。
(2)
3問中ちょうど1問正解した生徒の人数を求めなさい。
(3)
この試験の得点の度数分布表としてあり得るものは下の3通りです。
空欄をうめなさい。

@解説@
(1)
2番と3番の各配点と正解者数がわかっている。
(2番の総得点)+(3番の総得点)
=3×14+5×14
=8×14=112点
クラス全体の総得点は、5.68×25=142点
1番の総得点は、142-112=30点
1番の配点は2点だから、正解者は30÷2=15人
(2)
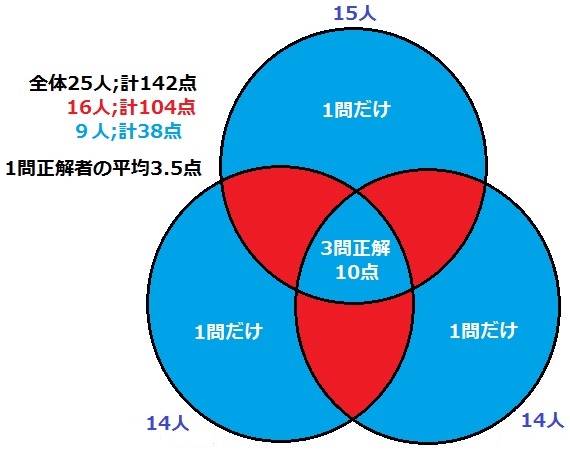
ベン図で整理するとこうなる。
2問正解者の総得点は、6.5×16=104点
1問正解者と3問正解者の総得点は、142-104=38点
その人数は、25-16=9人
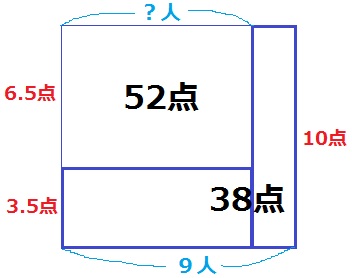
鶴亀算。
1問正解者の得点は均して、いずれも3.5点とする。
左上の長方形は、9×10-38=52点
1問正解者は、52÷(10-3.5)=8人
(3)
●8点が2人●
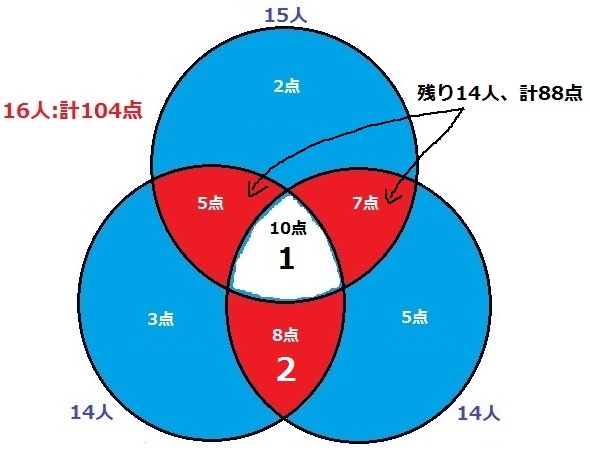
前問より、真ん中の3問正解者は1人と確定する。
8点が2人のとき、残りの2問正解者は14人、88点。
鶴亀算を解くと、5点が5人、7点が9人。
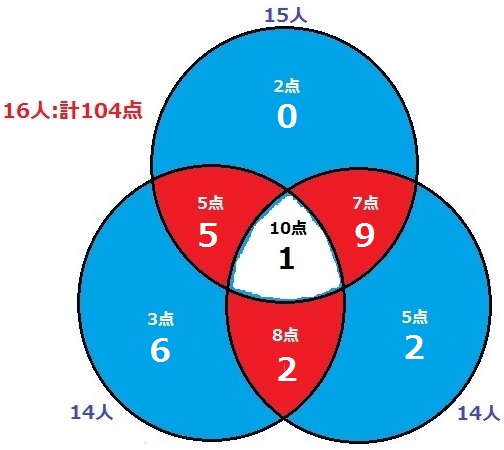
あとは3つの円をみれば、それぞれの1問正解者の人数が確定する。
1番だけ正解…15-(5+1+9)=0人
2番だけ正解…14-(5+1+2)=6人
3番だけ正解…14-(9+1+2)=2人
●8点が4人●
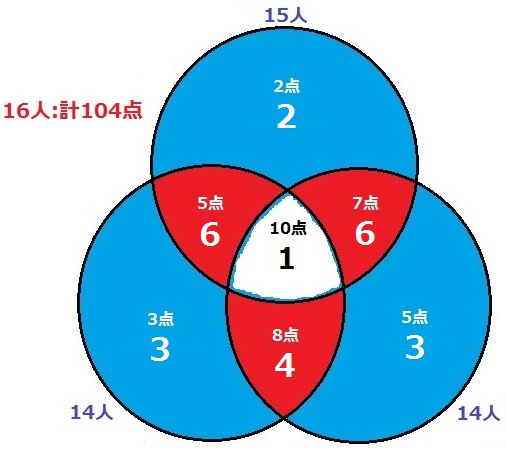
同様の処理を繰り返す。
2問正解者の残りは12人、72点。
鶴亀算を解いて6人ずつ。1問だけの正解者をだす。
●8点が6人●
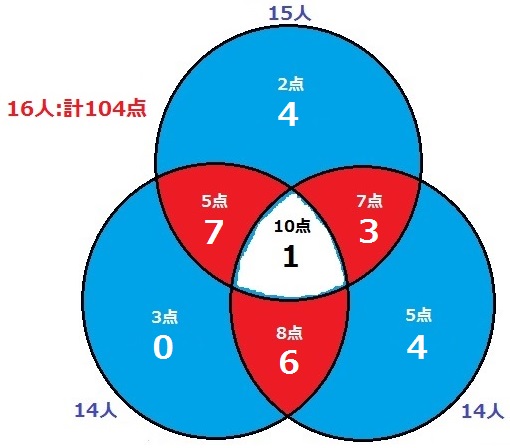
2点の正解者は残り10人、56点。
鶴亀算を解いて7人と3人。計算すると上のベン図になる。

5点は2ヶ所あるので合計する。



コメント