問題PDF
A君は自転車に乗ってP駅を出発し、線路沿いの道を一定の速さでQ駅に向かいました。A君が出発してから3分後に、電車がP駅を出発してQ駅に向かいました。電車がA君の4倍の速さでP駅とQ駅の間を何回か行ったり来たりし、各駅に着くと5分間停車するものとします。
〔図1〕のグラフは、A君がP駅を出発してからQ駅にたどり着くまでの時間と、A君と電車との間の距離の関係を表したものです。このとき、後の問いに答えなさい。
ただし、線路や道は一直線で、道の幅や自転車、電車の長さは考えないこととします。

(1)
A君が電車に初めて後ろから追い越されるのは、A君がP駅を出発してから何分後ですか。
(2)
A君がQ駅にたどり着いたのは、A君がP駅を出発してから何分後ですか。
(3)
A君が電車と初めて正面から出会うのは、A君がP駅を出発してから何分何秒後ですか。
(4)
〔図1〕の(ア)にあてはまる数と(イ)にあてはまる数の比を求めなさい。
@解説@
(1)

3分後に電車がP駅を出発。電車がAを追い越してQ駅に5分停車。
電車とAが向き合い、途中で出会う。電車がP駅に5分停車。電車がAを追いかける。
グラフの最後でAがQ駅に到着したときに0m。ということは、電車も同時にQ駅に到着する。
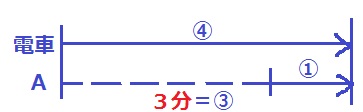
距離の比(速さの比)は、A:電車=①:④
Aは③を3分で移動するので、Aが電車に追い越された④は4分後。
(2)
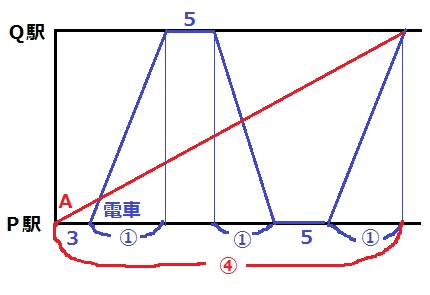
ダイヤグラムに変換する。
時間の比は、A:電車=④:①
電車が片道にかかる時間①が3本あり、全体の時間が④である。
③+3+5×2=④
①=13
AがQ駅に着く④は、13×④=52分後
(3)

電車の片道①が13分。これを頼りに時間を確定すると、うえのようになる。
電車とAが出会うのは●のところ。
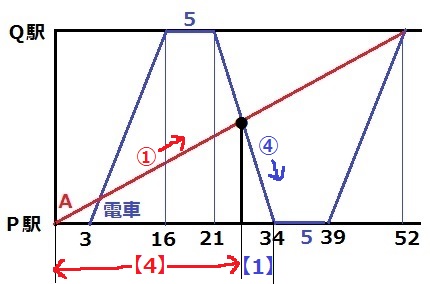
●から垂線をひく。
時間の比はA:電車=4:1だから、34×4/5=27.2分=27分12秒後
(4)
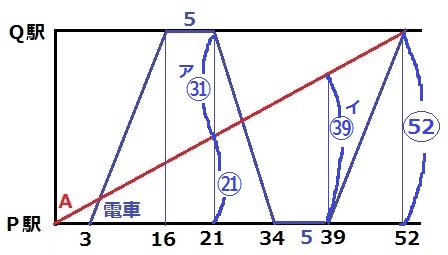
全体の距離を〇52とする。
39分後のAと電車の距離(イ)は㊴。
21分後のA-P駅間の距離が㉑だから、Aと電車の距離(ア)は㉛。
したがって、ア:イ=31:39



コメント