問題ＰＤＦ
家と公園の間に図書館があります。
ＡさんとＢさんが家から公園までそれぞれ一定の速さで歩きます。
Ａさんは、家から公園まで20分かかります。
Ａさんが家から図書館まで歩くのにかかった時間と、
Ｂさんが図書館から公園まで歩くのにかかった時間の合計は22分です。
また、Ｂさんが家から図書館まで歩くのにかかった時間と、
Ａさんが図書館から公園まで歩くのにかかった時間の合計は23分です。
このとき、次の各問いに答えなさい。
（１）
Ｂさんが家から公園まで歩くのにかかった時間は何分ですか。
（２）
Ａさんが家から図書館まで歩くのにかかった時間は何分ですか。
（３）
ＡさんとＢさんが家を同時に出発し、
また同時にＣさんが分速360ｍで走る車で公園を出発し家へ向かいました。
また、ＢさんはＡさんとＣさんが出会った地点を、
ＡさんとＣさんが出会ってから１分後に通過しました。
家から公園までの距離は何ｋｍですか。
＠解説＠
（１）
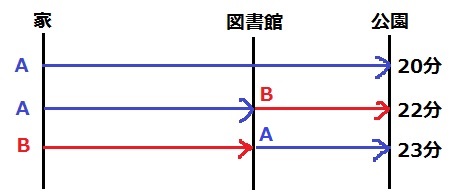
青がＡ、赤がＢ。
１本目と２本目、１本目と３本目を比較してみよう。
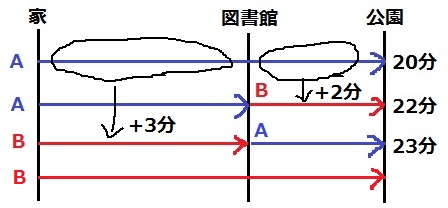
家～図書館で、Ａ→Ｂに変えると＋３分。
図書館～公園で、Ａ→Ｂに変えると＋２分。
家～公園で、Ａ→Ｂに変えると＋５分。よって、25分。
（２）
ＡとＢは速さが一定。
同じ速さだと、時間の比と距離の比は比例。
進む距離が長くなるほど、それに応じて２人の時間差を比例して大きくなるので、
時間の差も距離の比と比例にある。
家～図書館で３分の差、図書館～公園で２分の差が生じるということは、
家～図書館と図書館～公園までの距離の比は３：２。
Ａは家～公園まで20分かかるので、家～図書館までは、20×３/５＝12分
（３）
距離を求めるので、Ｃの分速360ｍを使う。
ＡとＣが出会ってから１分後に、Ｂがその地点に着くということは、
ＡとＣが出会うときにＡとＢは１分の差が生じた。
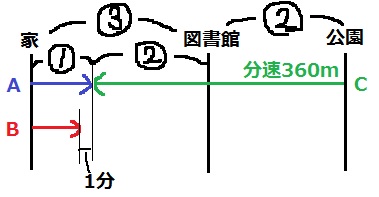
前問の同様、『時間の差の比が距離の比』から、
ＡとＢは図書館で３分差で、ＡとＣが出会う地点で１分差が生じるので、
家～図書館までの距離を③とすると、家～ＡとＣが出会う地点は①。
Ａは⑤の距離を20分で歩くので、ＡとＣが出会う地点までの①は４分。
Ｃは④の距離を４分で走るから、家～公園まで距離⑤は、
分速360ｍ×４分×⑤/④＝1800ｍ＝1.8ｋｍ
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント