2018年度　早稲田中学２回目過去問【算数】大問３解説

問題ＰＤＦ
５月のカレンダーがあります。○の位置にある７つの数は91になりました。
次の問いに答えなさい。

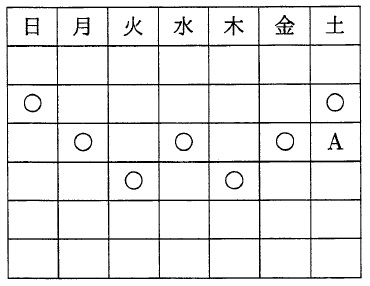
（１）
Ａの位置にある数はいくつですか。

（２）
この年の11月３日は何曜日ですか。

（３）
この年の１月から５月までのカレンダーで、土曜日にならんでいる数の和を考えます。
その和は２通り考えられますが、小さい方の和はいくつですか。

＠解説＠
（１）

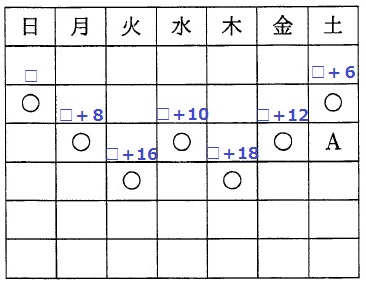
最小値を□とおいて、すべてを□で表す。
□＋（□＋６）＋（□＋８）＋（□＋10）＋（□＋12）＋（□＋16）＋（□＋18）
＝７×□＋70＝91
□＝３

□＋12＝３＋12＝15日となり、Ａは翌日なので16。

＠別解＠
左右対称なので、真ん中の水曜日に集約させる。

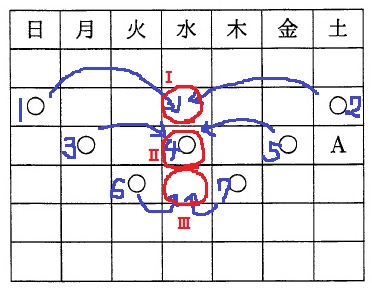
Ⅰ→１と２の平均→１＋２の和がⅠの２倍。
Ⅱ→３と５の平均→３＋５の和がⅡ（４の値）の２倍。
Ⅲ→６と７の平均→６＋７の和がⅢの２倍。

さらに、ⅡはⅠとⅢの平均→Ⅰ＋Ⅲの和がⅡの２倍。
すべてをⅡに集めると、４＋（１＋２）＋（３＋５）＋（６＋７）
＝４＋Ⅰ×２＋Ⅱ（４）×２＋Ⅲ×２
＝４×３＋（Ⅰ＋Ⅲ）×２
＝４×３＋Ⅱ（４）×４
＝４×７＝91
４＝13
４が13日なので、Ａは16日となる。

（２）
５月３日は日曜日。

各月の日数をうしろから求めてみる。
11月は３日間。
10月は31日、９月は30日、８月は31日、７月は31日、６月は30日、５月は31日。
合計→187日
11月３日は、言い換えると５月187日になる。

５月３日～５月187日は、187－３＋１＝185日間
185÷７＝26…３
ループは日曜から始まり、土曜で終わるので、余り３は日・月・火。
よって、11月３日は火曜日。

（３）
５月２日が土曜日。

問題は、平年かうるう年かで１月と２月の日にちがズレること。
仮に平年とすると、１月…31日、２月…28日、３月…31日、４月…30日。
合計120日間
５月２日が土曜なので、これを基準にさかのぼると、
122÷７＝17…３
ループは土からさかのぼって日に終わるので、余り３は土・金・木。
元日（１月１日）は木曜となる。

ということは、１月の土曜は〔３・10・17・24・31〕２月は〔７・14・21・28〕
うるう年だと１個ズレるので、１月の土曜は〔４・11・18・25〕２月は〔１・８・15・22・29〕
うるう年は各々の日にちに＋１日されるが、平年では１月31日が登場するので値が大きくなる。
よって、うるう年を選択する。

１月〔４・11・18・25〕→58
２月〔１・８・15・22・29〕→75
３月〔７・14・21・28〕→70
４月〔４・11・18・25〕→58
５月〔２・９・16・23・30〕→80
計算のコツは並び替えて２倍する。
（４月だったら、（４＋25）＋（11＋18）＝29＋29＝58）
58＋75＋70＋58＋80＝341日
*戦略としては３月１日まで（計算で）一気に遡ってもＯＫ。
３月１日が日曜日と確定。平年だと２月28日、閏年だと29日が土曜となり、１月まで手動で戻る。
決め手は１月の最後の土曜日にあると気づけば、あとは足し算のみ。
難関中（算数科）解説ページに戻る