2018年度　函館ラ・サール中学過去問【算数】大問３解説

問題ＰＤＦ
下の図のような直線上を、秒速３ｃｍの速さで動く点Ｐと、
秒速２ｃｍの速さで動く点Ｑがあります。

点ＰがＡからＦに向かって出発するのと同時に、点ＱはＢからＦに向かって出発します。
ＰがＢに来たときＱはＣに着き、ＰがＣに来たときＱはＤに着き、
さらにＰがＤに来たときＱはＥに着き、その後はＰもＱも同時にＦに着くものとします。
（１）
ＤＦの長さは、ＥＦの長さの何倍ですか。

（２）
点ＱがＤからＥまで行くのに４秒かかりました。ＥＦの長さは何ｃｍですか。

（３）
（２）のとき、点ＰがＡからＦまで行くのに何秒かかりますか。

＠解説＠
アキレスと亀みたいに、なかなか追いつけないＰ…。
（１）
ＰがＤ、ＱがＥにいるときを考える。

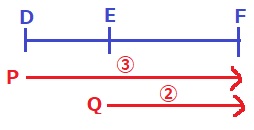
ここからＦに同時に到着する。
速さの比と距離の比は比例なので、ＤＦを③とするとＥＦは②になる。
ＤＦはＥＦの３/２倍。

（２）
ＤＥ＝秒速２ｃｍ×４秒＝８ｃｍ
先ほどの図より、ＤＥ＝①
ＥＦ＝８×２＝16ｃｍ

（３）

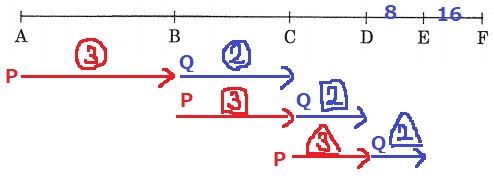
これが見えれば正解も近い。
ＣＤ＝８×３/２＝12ｃｍ
ＢＣ＝12×３/２＝18ｃｍ
ＡＢ＝18×３/２＝27ｃｍ
Ａ～Ｆまでの距離は、27＋18＋12＋８＋16＝81ｃｍ
よって、81÷３＝27秒

＠別解＠
ＰとＱは同時に出発して同時にＦへ到着するので、
ＰがＡ～Ｆまで行く時間と、ＱがＢ～Ｆまで行く時間は同じ。

ＱはＤ－Ｅ間の移動に４秒かかるので、Ｅ－Ｆ間は８秒。
Ｃ－Ｄ間は４×３/２＝６秒
Ｂ－Ｃ間は６×３/２＝９秒
よって、９＋６＋４＋８＝27秒
難関中（算数科）解説ページに戻る