2018年度　市川学園中学過去問【算数】大問６解説

問題ＰＤＦ
図１のように、長方形ＡＢＣＤがあり、ＡＢ＝８ｃｍ、ＡＤ＝12ｃｍです。点ＰとＳは、この長方形のたての２等分、点Ｑ、Ｒ、Ｔ、Ｕは、この長方形の横を３等分する点です。ここで、図２のように長方形ＡＢＣＤの内部に点Ｅをとり、ＥＰ、ＥＱ、ＥＳ、ＥＴを引いて、長方形を４つの四角形に分けました。このとき、次の問いに答えなさい。

（１）
四角形ＥＴＡＰと四角形ＥＱＣＳの面積の和を求めなさい。

（２）
四角形ＥＴＡＰと四角形ＥＰＢＱと四角形ＥＱＣＳの面積の比が９：８：19のとき、
四角形ＥＳＤＴの面積を求めなさい。

＠解説＠
（１）

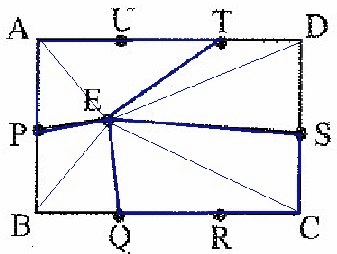
このような補助線をひく。
求めたいのは、四角形ＥＴＡＰ（左上）と四角形ＥＱＣＳ（右下）の和だが、
△ＡＤＥ＋△ＢＣＥ、△ＡＢＥ＋△ＤＣＥで捉えるのがポイント！

△ＡＤＥ＋△ＢＣＥを等積変形すると、長方形の半分になる。
△ＡＢＥ＋△ＤＣＥも同様に等積変形すると、同じく長方形の半分になる。
各々、８×12÷２＝48ｃｍ²

高さが一定なので、面積比は底辺の比にあたる。
△ＡＤＥ＋△ＢＣＥ（左図）において、
△ＥＡＴ＋△ＥＣＱ：△ＥＤＴ＋△ＥＢＱ＝ＡＴ＋ＣＱ：ＤＴ＋ＢＱ＝２：１

△ＡＢＥ＋△ＤＣＥ（右図）において、
△ＥＡＰ＋△ＥＣＳ：△ＥＢＰ＋△ＥＤＳ＝ＡＰ＋ＣＳ：ＢＰ＋ＤＳ＝１：１

求めるべき四角形ＥＴＡＰと四角形ＥＱＣＳの和は、
（△ＥＡＴ＋△ＥＣＱ）＋（△ＥＡＰ＋△ＥＣＳ）
＝48×２/３＋48×１/２＝56ｃｍ²
斜めの組み合わせに着目して、底辺の比から面積比を計算する。

（２）
前問ができればラクラク解ける。

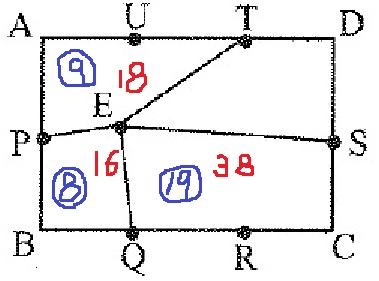
⑨＋⑲の和が56ｃｍ²なので、ここから３つの四角形の面積を調べる。
全体から３つの四角形をひけばいい。
８×12－（18＋16＋38）＝24ｃｍ²
難関中（算数科）解説ページに戻る