問題PDF
一定の速さで流れる川の下流にあるA地点と、上流にあるB地点の間を
太郎くんと次郎くんが2人乗りボートに一緒に乗って移動します。
静水でボートをこぐ速さが、太郎くんは分速50mで、次郎くんは分速38mです。
最初に太郎くんがこぎ始め、交互に8分ずつこいでA地点からB地点までを往復しました。
すると、A地点からB地点までは112分かかり、B地点からA地点までは64分かかりました。
次の問いに答えなさい。ただし、交代にかかる時間は考えないものとします。
(1)
川の流れの速さは分速何mですか。
(2)
B地点からA地点に戻る途中に、ペットボトルを川に落としました。
2人がA地点に戻ってきてから65分後に、落としたペットボトルがA地点に流れてきました。
ペットボトルを落としたのは、2人がA地点に到着する何分前ですか。
(3)
太郎くんを乗せたまま、次郎くんが「13分こいだら2分休む」を繰り返しながら、
A地点からB地点までを1人でこぐとき、何分かかりますか。
@解説@
(1)
太郎と次郎は8分ずつこぐ。
太郎+次郎=16分のかたまりで考えると、
上りは112÷16=7回、下りは64÷16=4回と整数値になり、
次郎がちょうどこぎ終わったときにB地点やA地点に到着する。
太郎+次郎の上りと下りの速さの比は逆比で4:7。
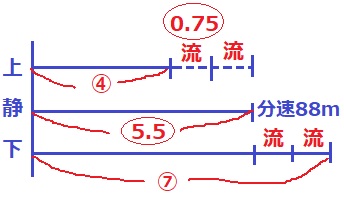
静水時の速さは、(④+⑦)÷2=〇5.5
〇5.5が分速88mにあたる。
留意すべき点は、太郎と次郎を合わせた速さなので川の流れが重複する!
(上りの速さ=(太-流)+(次-流)=太+次-流×2)
川の流れは、(〇5.5-④)÷2=〇0.75
よって、川の流れは、88×〇0.75/〇5.5=分速12m
(2)
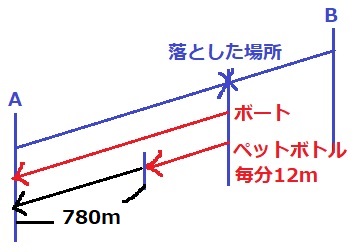
ペットボトルは川の流れと同じ、毎分12mで進む。
ボートがA地点に着いたとき、ペットボトルは12×65=780m後方にある。
問題は、ボートは8分おきに速さが変わること。。
ペットボトルを落とした瞬間、太郎と次郎のどちらが何分こいでいたのかわからない。
そこでボートがA地点に到着してから逆算して8分前を検証する。

最後は次郎がこぐ。
次郎の下りの速さは、38+12=分速50m
ボートはA地点から、50×8=400m後方へ。
ペットボトルは12×8=96m後方へ。
両者はまだ距離があるので、さらに8分前を検証…。
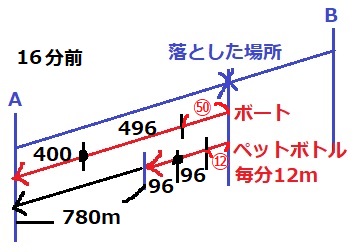
太郎の下りの速さは、50+12=分速62m
ボートは62×8=496m後方へ。
ペットボトルは先ほどと同様、96m後方へ。
両者の距離は、(780+96+96)-(400+496)=76m
ペットボトルを落としたときは次郎がこいでいた。
ここで、速さの比=距離の比を使う。
次郎:ペットボトル=㊿:⑫
差の㊳が76mにあたる。
⑫=76×⑫/㊳=24m
24÷12=2分間
よって、ペットボトルを落としたのは、8+8+2=18分前
(3)
太郎の上りは、50-12=分速38m
次郎の上りは、38-12=分速26m
8分ずつの交代を7回してB地点に行くので、
AB間の距離は(38+26)×8×7=3584m
次郎は13分こいで2分休む。
15分で進む距離は、26×13-12×2=314m
3584÷314=11…130
(15分の固まりが11回+130m)
15×11+130÷26=170分



コメント