問題ＰＤＦ
図のように３×３のマス目に１から９までの数字が書かれたカードがあります。
また、１から９までの数字が１つずつ書かれたボールが入っている箱があります。
このとき、次のようなゲームをおこないます。
＠ルール＠
①箱からボールを１個取り出し、ボールに書かれた数字と同じ数字のマス目に〇を付ける。
ただし、一度取り出したボールは箱にもどさないものとする。
②①をくり返して、９個のマス目のうち、たて、横、ななめのいずれか一列の数字
すべてに〇が付いたら終了とする。
たとえば、１、２、４、３の順でボールと取り出すと、１、２、３の列の数字すべてに〇が付くので、ボールを４個取り出してゲームは終了となります。
また、１、２、３の順でボールと取り出す場合と１、３、２の順でボールを取り出す場合は、ともに１、２、３の列の数字すべてに〇が付くので、ボールを３個取り出してゲームは終了となりますが、これらは異なるボールの取り出し方とします。このとき、次の各問いに答えなさい。
（１）
３個のボールを取り出し、１、５、９に〇が付いてゲームを終了するような取り出し方は
何通りありますか。
（２）
４個のボールを取り出し、１、５、９に〇が付いてゲームを終了するような取り出し方は
何通りありますか。
（３）
５個のボールを取り出し、１、５、９の列の他にもう１列の数字すべてに〇が付いて
ゲームが終了するような取り出し方は何通りありますか。
＠解説＠
（１）
〔１・５・９〕を取り出してビンゴ。
３つの順列→３×２×１＝６通り
（２）
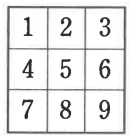
〔１・５・９・□〕を取り出し、１－５－９でビンゴ。
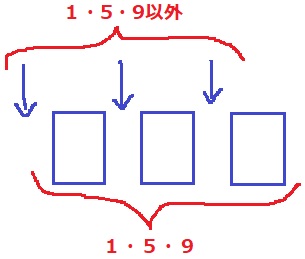
最後の４回目は１・５・９のどれかでなくてはならない。
この３つの並びは６通り。
１or２or３回目に１・５・９以外の６つの数字のどれかが入る。
６×３＝18通り
よって、６×18＝108通り
（３）
最後の５回目は、１・５・９のどれかでなくてはならない。
Ａ：１でフィニッシュ。
〔２・３〕か〔４・７〕を出す。
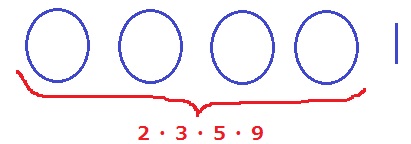
〔２・３〕を出す。
２・３・５・９の順列→４×３×２×１＝24通り
〔４・７〕も同様で24通りだから、計48通り。
Ｂ：９でフィニッシュ。
これもＡと対称的に考えて48通り。
Ｃ：５でフィニッシュ。
〔２・８〕〔３・７〕〔４・６〕がある。
24×３＝72通り
したがって、48＋48＋72＝168通り
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント