2018年度　海城中学過去問【算数】大問４解説

問題ＰＤＦ
図１のように、中心が点Ｐで半径１ｃｍの円Ｐと、中心が点Ｑで半径２ｃｍの円Ｑがあります。
円Ｐの周上には２点Ａ、Ｂが、円Ｑの周上には点Ｃがあり、角ＡＰＢは90°です。
この２つの円を図２のように、点Ｂと点Ｃが重なるように置き、
円Ｐを円Ｑの内側をすべらないように、矢印の方向へ転がします。

（１）
図３のように、角ＣＱＰが45°になるまで転がしたとき、
点Ａ、Ｂの位置を解答用紙の図にかき入れなさい。

（２）
角ＣＱＰが60°になるまで転がしたとき、角ＢＰＱの大きさを求めなさい。

（３）
円Ｐが円Ｑの内側をちょうど１周してもとの位置に戻ってくるまでに、
点Ｂの動いた道のりを求めなさい。

＠解説＠
（１）
位置関係の把握。
円Ｑに内接するように円Ｐを45°回転する。
２つの円が接した弧の部分に注目！

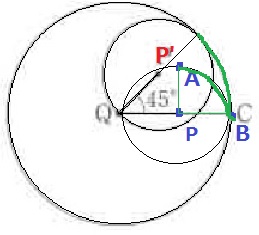
スタート～45°まで円Ｐが移動したとき、
円Ｐが円Ｑと接した緑の弧の長さが等しくなる。
円Ｐの半径は１ｃｍ、円Ｑの半径は２ｃｍで、円周の比は円Ｐ：円Ｑ＝１：２
円Ｑの円周における８分の１円（中心角45°）は、円Ｐの４分の１円に相当する。
つまり、円Ｐでいえば、Ｂ（Ｃ）からＡの弧の長さとなる。
→Ａが移動先の円Ｐ’において円Ｑと接する点。

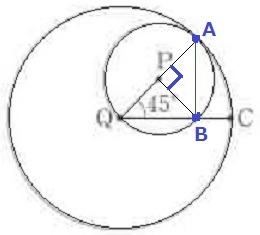
ＱＰを延長して、円Ｑの円周との交点がＡ。
そこから時計回りに90°のところにＢ。
△ＰＢＱが45°－45°－90°の直角二等辺三角形で、
半径ＡＰ＝ＢＰ＝ＱＰから、△ＡＢＱも直角二等辺とわかる。
すなわち、∠ＡＢＱ＝90°で、ＡＢとＱＣが垂直の関係。
ＢはＱＣ上にあり、円Ｐの円周と線分ＱＣの交点にあたる。

（２）
円Ｐを60°回転させる。

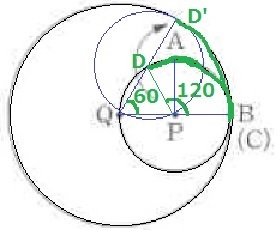
円Ｑと移動先の円Ｐ’の接点をＤ’とする。
２本の緑の弧は同じ長さ。
弧ＢＤ’は円Ｑの６分の１円だから、スタート地点の円ＰにおいてＤＢは円Ｐの３分の１円。
∠ＤＰＢ＝120°
∠ＤＰＡ＝120－90＝30°
すなわち、Ｄから時計回りに30°の場所にＡがある。

これは移動先の円Ｐ’でも同様。
Ｄ’から時計回りに30°がＡ’→∠Ｄ’Ｐ’Ａ’＝30°
∠ＡＰＢ＝90°の位置関係も同様→∠Ａ’Ｐ’Ｂ’＝90°
∠Ｂ’Ｐ’Ｑ＝180－（30＋90）＝60°

（３）
点Ｂがどのような軌跡をたどるか(;`ω´)
点Ｂは円Ｑに内接しながら回転する円Ｐの円周上の点。
前問の結果を見てみよう。

円Ｐが45°移動したとき、Ｂの移動先Ｂ’はＱＣ上にいた。

円Ｐが60°移動したとき、Ｂ’はＱＣ上で先ほどと比べて左側にいそうな気がする…。
∠Ｐ’ＱＢ’＝∠Ｂ’Ｐ’Ｑ＝60°なので、△Ｐ’Ｂ’Ｑは正三角形。
Ｂ’はＰと重なる…。

Ｂは真横に移動してんじゃあ・・？

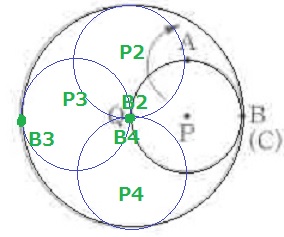
Ｐ２は90°動いたとき。円Ｑ４分の１回転→円Ｐ２分の１回転。
Ｂの反対側の点が点Ｑに接して真上にくるので、Ｂは真下（円Ｑの中心）にくる。

Ｐ３は180°動いたとき。円Ｑ２分の１回転→円Ｐ１回転。
Ｂが円Ｑに接するので、Ｂは左側にくる。

Ｐ４は270°動いたとき。円Ｑ４分の３回転→円Ｐ３分の２回転。
Ｂの反対側の点が点Ｑに接して真下にくるので、Ｂは真上（円Ｑの中心）にくる。

結局、Ｂは円Ｑの直径を往復する。
したがって、８ｃｍ。

＠トロコイド曲線＠
本問はたまたま直線でありがたかったが、
円を曲線の図形に沿ってクルクルと回転させたとき、
回転させた円の定点の軌跡をトロコイド曲線という。

内トロコイドその1。
大円の半径は5で、小円の半径は2です。
内サイクロイドの時の点と、小円の中心の中点の軌跡です。
丸い星型ですね。#数学GIF pic.twitter.com/3zKpnhHwlV

— 数学GIF画像bot (@math_gif) September 22, 2016

外側をコロコロ回転すると外トロコイド、内側をコロコロ回転すると内トロコイド。
上の例では、小円の半径の中点を定点として、その軌跡を描いています。
こういう幾何学もあるんですねぇ(ﾟДﾟ)ﾎｩ