問題PDF
ある中学校の行事「A川歩行」では、A川に沿って数百人の生徒が一列になって一定の速さで歩きます。
今年は川上の左岸のP地から、A川に垂直にかかった全長800mのB橋を一回だけ渡って、川下の右岸のQ地まで歩きます。
列の先頭はP地を午前9時30分に出発しました。列の長さは、列の最後尾が歩き始めるときに1.6kmになりました。この列はB橋を渡り始めてから渡り終えるまでに30分かかり、列の先頭は午前11時ちょうどに渡り終えました。B橋を渡り終えるとすぐに広い土手があって、着いた生徒から昼食休憩をとりました。その後、正午にB橋を渡り終えた場所から再び列の先頭が出発し、時速3.6kmで歩きました。このときも、列の長さは1.6kmになりました。列の先頭がQ地に着いたのは午後2時40分でした。
また、ボートが午前8時55分にQ地を出発しました。このボートは午前9時55分に生徒の列の先頭と出会いました。A川の流れの速さを時速2kmとして、次の問いに答えなさい。
(1)
昼食休憩をとる前の生徒の列の速さは時速何kmでしたか。
(2)
ボートの静水時の速さは時速何kmですか。
(3)
ボートはQ地から31km上流にある右岸のR地に停泊して、そこで昼食休憩をとり、
午前11時50分に下流へ向けて出発しました。
ボートが生徒の列の最後尾に追いつくのは午後何時何分ですか。
@解説@
(1)

1.6kmの電車が0.8kmの橋を通過する問題と同じ。
0.8+1.6=2.4kmを30分(1/2時間)で歩くので、2.4×2=時速4.8km
(2)

状況を整理する。
先頭だけの時刻を追うと上図のようになる。
橋の長さ0.8kmはPQ間の距離に含まれないことに注意!

P~休憩ポイントまでは、4.8×3/2時間=7.2km
P~橋までは、7.2-0.8=6.4km
橋~Qの距離は、3.6km×8/3時間=9.6km
PQ間の距離は、6.4+9.6=16km
先頭が出発してから25分後にボートと出会う。
その距離は、4.8×25/60時間=2km
ボートは1時間で16-2=14km移動した。
上りの速さが時速14kmで、これに流速の時速2kmを足し、
静水時の速さは時速16km。
(3)
ボートが列の最後尾に追いつく時間を求めるが、
最後尾がB橋を出発した時刻が正午から4/9時間後と変な数字がでてくる(;°;ω;°;)
列の先頭は正午発とキリが良いので、先頭を基準に考えてみる。

ボートは午前11時50分にRを発つ。
前問でボートの静水時が時速16kmだったので、下りの速さは時速18km。
正午までボートは18×1/6時間=3km移動している。
列の先頭との差は、31-(3+9.6)=18.4km
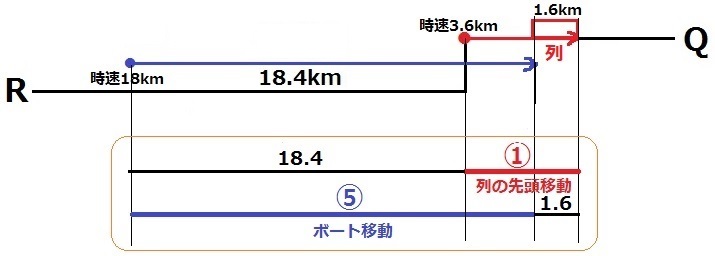
↑正午からボートが列の最後尾に追いつくまでの様子。
速さの比が、ボート:列=18:3.6=⑤:①に注目する。
時間一定ならば、速さの比は距離の比。
ボートの出発地点から列の先頭地点までの全体を見渡すと、
ボートの移動距離⑤+1.6km=18.4km+列の先頭移動距離①
④=16.8km
①=4.2km
列が移動した時間は、4.2÷3.6=7/6時間=1時間10分
正午から1時間10分後である午後1時10分。
@備考@
列の最後尾基準で考えて、正解にたどり着けなかった人もいたと思いますので、
以下、計算過程を残しておきます。
列の最後尾がB橋を出発した時刻は、正午から1.6÷3.6=4/9時間後
この間にボートは、1/6+4/9=11/18時間移動している。
移動距離は、11/18×18=11km
ボートと最後尾との差は、31-(11+9.6)=10.4km
先ほどの速さの比=距離の比=⑤:①を用いる。
④=10.4kmだから、最後尾の移動距離①=2.6km
その時間は、2.6÷3.6=13/18時間
正午から4/9+13/18=7/6時間=70分後→午後1時10分
@余談@
>利根川歩行・荒川歩行(早稲田中高)
A川は荒川でしょうか?



コメント