問題PDF
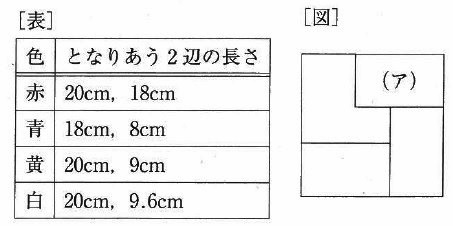
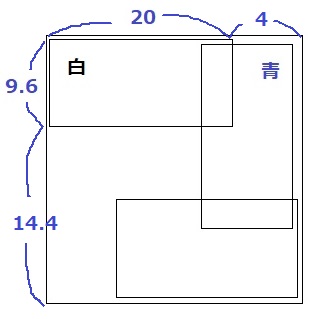
赤、青、黄、白の長方形の紙が1枚ずつあり、それぞれのとなりあう2辺の長さは表のようになっています。この4枚を一部が重なるようにして図のように並べて1つの正方形を作ったとき、見えている部分の面積が4色すべて等しくなりました。このとき、次の問いに答えなさい。
(1)
図の一番上にある、(ア)の紙の色は何色ですか。
また、作った正方形の1辺の長さを求めなさい。
(2)
図の並べ方について、紙の色を下から順に答えなさい。
(3)
紙の並べ方を図と変えて、図と同じ大きさの正方形を作ったところ、
見えている部分の面積は、青が105.6cm2、黄が156cm2になりました。
この並べ方について、紙の色を下から順に答えなさい。
また、赤の見えている部分の面積を求めなさい。
@解説@
(1)
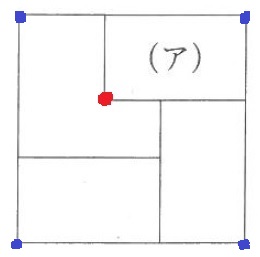
赤い頂点に注目する。
4枚の長方形の1つの頂点は、それぞれ正方形の四隅に配置されているが、
四隅の頂点の反対側にある(ア)の赤い頂点がむき出しになっているということは、
(ア)はすべて表にでており、一番上にある長方形。
最も面積の小さい青が一番上でないと、見えている4ヶ所の面積は等しくならないので、
(ア)が青となる。
青の面積…18×8=144cm2
正方形の面積…144×4=576cm2
576=24×24ゆえ、正方形の1辺は24cm。
*144が12の平方数なので、それに2の平方数である4をかければ12×2=24の平方数になる。
(2)
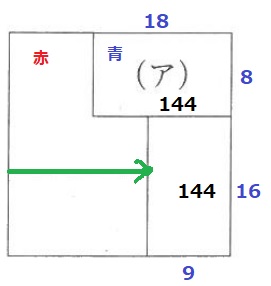
左上の正方形っぽいのが赤。下2枚が黄か白。
面積が144cm2、正方形の1辺が24cmなので、右下の長方形の横が9cmとなる。
緑の矢印に注目しよう。
途中で矢印が途切れているということは、下2つの長方形では右側が上にくる。
ということは、右下の長方形の横は9cmなので黄色。
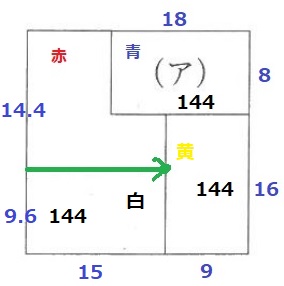
左下が白で、縦の長さは144÷15=9.6cm
白の縦の長さがフルに出ていることになり、赤が一番下になる。
整理すると下から順に、赤→白→黄→青
(3)
青は18×8-105.6=38.4cm2、黄色は20×9-156=24cm2面積が減少している。
一番上にくるのは赤と白のどちらだろう?
赤の見えている部分の面積を求めるので白だろうと想像できるが、
仮に赤を一番上にすると、赤以外の面積が24×24-20×18=210cm2しかなく、
青と黄色の見えている部分の合計を下回ってしまうので不適。
よって、一番上は白。
正方形の1辺は24cm。
4つの長方形は正方形の四隅に配置する。
青の減少が38.4cm2と端数がでているので、青と白はダブっているはず。

白と青がダブる長方形の横は、8-4=4cm
9.6×4=38.4cm2となるので、青の面積が減少するのはココしかない。
→青と黄色では青の方が上にくる。
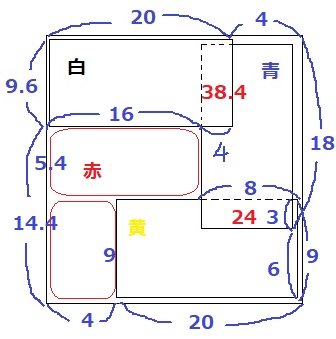
計算していくと、青と黄色のダブりは24cm2となる。
黄色の減少はここしかないので、赤と黄色では黄色が上にくる。
下から順番に、赤→黄→青→白。
見えている赤の部分は、4×9+16×5.4=122.4cm2



コメント