2021年度　麗澤中学過去問【算数】大問３解説

問題ＰＤＦ
ある場所で、春分の日の影のでき方について調べました。
図１は点Oから見た太陽の動きを表しています。

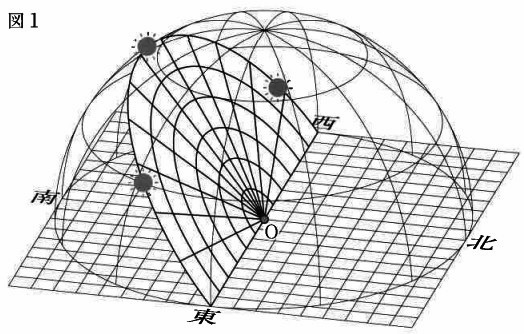
図２のように、地表から高さ60ｃｍの位置に直方体ABCDEFGHの底面EFGHを固定し、ＡＢ＝ＡＤ＝30ｃｍ、ＡＥ＝20ｃｍとなっていて、図４のように太陽の光は平行に降り注ぐことがわかっています。図５は図４を真上から見た図です。10：00には図２のように点Ｃの影が点Ｐに落ち、15：25には図３のように点Ｃの影が点Ｑに落ちるとするとき、次の問いに答えなさい。

（１）
10：00時点の直方体の影の面積を求めなさい。

（２）
10：00時点の直方体の影の輪郭は、６つの辺ＢＣ、ＣＤ、ＤＨ、ＥＨ、ＥＦ、ＢＦの影です。
15：25時点の直方体の影の輪郭は、どの辺の影であるか６つ選んで解答用紙の□に印をつけなさい。

（３）
10：00から15：25の間に直方体の影が通った部分の面積を求めなさい。

（１）

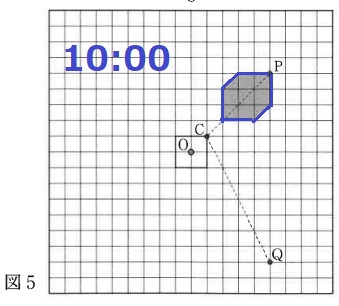
図２＝図４＝図５。図５の面積を求めればいい。
２つの直角二等辺三角形を合わせると８マス分。
15×15×８＝1800ｃｍ²

（２）

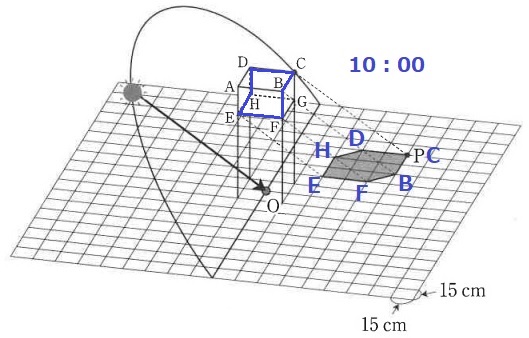
10：00を確認するとこうなる。
太陽に照らされた辺のうち、６辺がうしろの影へ移動する。

15：25ではこうなる。
本問は影を正確に描写できなくても正解できる。

（３）
ＡとＢの位置はわかりやすい。
光は平行に差すので、ＡＢ＝ＢＣ＝30ｃｍはそのまま平行移動するから、
Ｑ⇒Ｂ⇒Ａは２マス分ずつ離れる。

問題はＧがどこにくるか。

高さに注目する。三角形の相似を描くと、地面～Ｇ：ＧＣ＝60：20＝③：①
これを平面図でとらえると、ＣＱは横４マス、縦８マスの長方形の対角線だから、
ＣＧ’から横３マス、縦６マスの長方形の対角線に相当する。

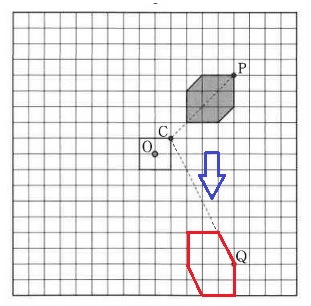
平行を頼りに残りを描写すると、15：25の影はうえのようになる。
ＣＰとＣＱの長さが違う。
半径が変動したら算数の範囲で解くのは難しそうだが…

ここで理科の知識です。
『春分の日の影』はまっすぐに進むので、求積すべき範囲は青線のエリアになる。
３×14マスの長方形から２つの三角形を取り除くと40.5マス分。
15×15×40.5＝5＝9112.5ｃｍ²

＠日影曲線＠
影の先端の軌跡を日影曲線という。

京都市青少年科学センターより、３地点の日影曲線。
上から夏至→春分・秋分→冬至。理科で狙われるので、しっかりおさえておこう。

では、なぜ春分・秋分の日影曲線はまっすぐになるのか？
この説明がキツイ(;´･ω･)

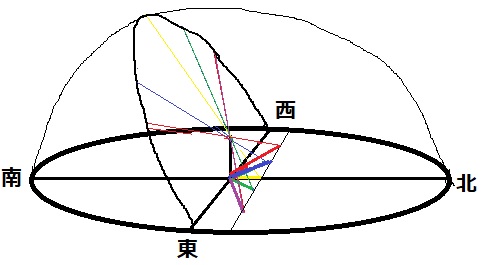
春分・秋分の太陽は真東からのぼり、真西に沈む。
太陽の南北方向と東西方向にかかる移動の比率で影の先端がまっすぐになるんだと思う…。
考えれば考えるほどよくわからん。

赤道の影がまっすぐになるのはわかりやすいので、そこが突破口だと思われる。
春分・秋分の日は赤道に対して太陽光が垂直に入る（南中高度が90°）。
23.4°の地軸の傾きを無視し、地球を球体として回転させると、
赤道からの距離（北緯）に応じて各棒の影が北へ平行移動して日影曲線がまっすぐになりそう。
難関中（算数科）解説ページに戻る