問題PDF
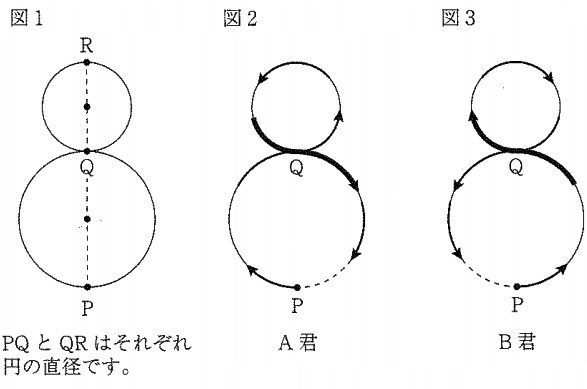
図1のように、大小2つの円を合わせた形をした平らなジョギングコースがあります。A君とB君はP地点から同時にスタートし、A君は図2のような向きで、B君は図3のような向きで、「8」の字をえがくようにこのコースをそれぞれ一定の速さで走り続けます。A君はB君より速く走ります。
また、CさんはA君、B君と同時にP地点からスタートし、大きな円のコースだけを反時計回りに一定の速さで歩き続けます。スタートした後、3人がはじめて同時に出会ったのはQ地点で、そのときまでにA君とB君は4回出会いました。図4は、スタートしてからの時間と、A君、CさんとP地点との道のり(P地点から進んだ道のりとP地点までの残りの道のりのうちの小さい方)の関係の一部を表しています。

このとき、次の各問いに答えなさい。
(1)
A君の走る速さは毎分何mですか。
また、小さな円のコースの1周の道のりは何mですか。
(2)
B君の走る速さとして考えられるもののうち、もっとも速い場合を考えます。
①このときのB君の速さは毎分何mですか。
また、3人がはじめて同時に出会ったのはスタートしてから何分後ですか。
②Cさんの歩く速さは毎分何mですか。
また、3人がはじめて同時に出会うときまでに、A君とCさんは何回出会いましたか。
@解説@
(1)

『P地点の道のり』はP地点までの距離。
Aのグラフの山頂はP地点から最も遠いR地点までの距離となる。
(言い換えれば、8の字コースの半周にあたる地点)
Aは8の字すべてを走るので、8の字(大円と小円)の全長は1500×2=3000m
Aはこれを15分で走るので、Aの速さは、3000÷15=分速200m
同様に、Cは大円のみを歩くので、大円は1000×2=2000m
よって、小円1周の道のりは3000-2000=1000m
(2)①
Bが最も速い場合を考える。
A・B・Cが同時にQ地点で会うまでに、AとBは4回会っている。
→3人が同時にQにきたとき、AとBの出会いは5回目。

5回目にQで出会うまでの経緯を考える。
仮にAとBがほぼ同じ速さだとすると、1回目はR付近、2回目はP付近、
3回目はR付近、4回目はP付近で出会うはず。
留意点は、AはBより速いので、Bより多く走らなくてはならないこと!
つまり、Aは下(P)から上がってRまで行き、Qまで下がり、
Bは上(P)から上がって両者がQで合流する。
Aの走る距離…3000(全周)×2+1500(半周)+500(R-Q間;小円の半周)=8000m
Bの走る距離…3000×2+1000(P-Q間;大円の半周)=7000m
距離の比は、A:B=8000:7000=8:7
速さの比は距離の比と等しく、Aは分速200mなので、
Bの速さは、200×7/8=分速175m
3人が出会う時間は、8000m÷分速200m=40分後
②
CはPから出発し、大円を反時計回りに歩く。
40分後、Qに到着するのでCが歩いた距離は、
1000m、3000m、5000m、7000m、9000m…
残りはグラフから手掛かりをつかむ。

CはAより遅いので、Cの歩く距離はAの8000mより短い。
Cが初めてQについた正確な時間はわからないが、10分~15分後にあるとわかる。
10分でつくと、1000÷10=分速100m
15分でつくと、100×2/3=分速200/3m
Cの速さは分速200/3~100mの範囲。
先ほどのCの歩いた距離の候補のなかでこの範囲に収まるのは、3000m÷40分=分速75mだけ。
よって、Cの速さは分速75m。
Aは8000m走り、Cは3000m歩く。

40分までに、Aは8の字を2周+1000m走り、Cは大円を1周+1000m歩く。
3人がはじめて同時に出会うまで、AとCは3回出会う。



コメント